5.4: Transformaciones lineales especiales en R²
- Page ID
- 114473
- Encontrar la matriz de rotaciones y reflexiones en\(\mathbb{R}^2\) y determinar la acción de cada uno sobre un vector en\(\mathbb{R}^2\).
En esta sección, examinaremos algunos ejemplos especiales de transformaciones lineales en la\(\mathbb{R}^2\) inclusión de rotaciones y reflexiones. Utilizaremos las descripciones geométricas de adición de vectores y multiplicación escalar discutidas anteriormente para mostrar que una rotación de vectores a través de un ángulo y la reflexión de un vector a través de una línea son ejemplos de transformaciones lineales.
De manera más general, denotan una transformación dada por una rotación por\(T\). ¿Por qué tal transformación es lineal? Considera la siguiente imagen que ilustra una rotación. Dejar\(\vec{u},\vec{v}\) denotar vectores.
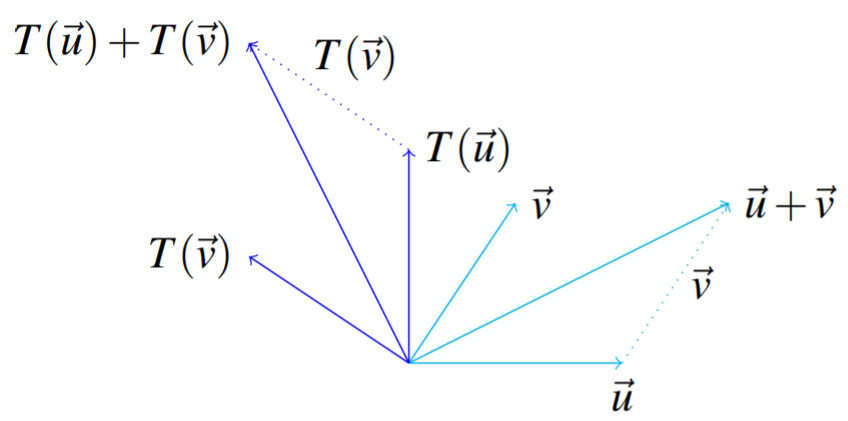
Consideremos cómo obtener\(T\left [ \vec{u}+\vec{v}\right ]\). Simplemente, agrega\(T (\vec{u})\) y\(T(\vec{v})\). He aquí por qué. Si agregas\(T(\vec{u})\) a\(T(\vec{v})\) ti obtienes la diagonal del paralelogramo determinada por\(T(\vec{u})\) y\(T(\vec{v})\), ya que esta acción es nuestra suma vectorial habitual. Ahora, supongamos que primero agregamos\(\vec{u}\) y\(\vec{v}\), y luego aplicamos la transformación\(T\) a\(\vec{u}+\vec{v}\). De ahí que nos encontremos\(T( \vec{u}+\vec{v})\). Como se muestra en el diagrama, esto dará como resultado el mismo vector. En otras palabras,\(T(\vec{u}+\vec{v}) = T(\vec{u}) + T(\vec{v})\).
Esto se debe a que la rotación conserva todos los ángulos entre los vectores así como sus longitudes. En particular, conserva la forma de este paralelogramo. Así ambos\(T\left [\vec{u}\right ]+T\left [\vec{v}\right ]\) y\(T\left [\vec{u}+\vec{v}\right ]\) dan el mismo vector. De ello se deduce que\(T\) distribuye a través de la adición de los vectores de\(\mathbb{R}^{2}\).
De igual manera, si\(k\) es un escalar, se deduce que\(T\left [k\vec{u}\right ]=kT\left [\vec{u}\right ]\). Así, las rotaciones son un ejemplo de una transformación lineal según la Definición 9.6.1.
El siguiente teorema da la matriz de una transformación lineal que gira todos los vectores a través de un ángulo de\(\theta\).
Dejar\(R_{\theta}: \mathbb{R}^2 \to \mathbb{R}^2\) ser una transformación lineal dada por vectores rotativos a través de un ángulo de\(\theta\). Entonces la matriz\(A\) de\(R_{\theta}\) viene dada por\[\left [ \begin{array}{rr} \cos \left [ \theta \right ] & -\sin \left [ \theta \right ] \\ \sin \left [ \theta \right ] & \cos \left [ \theta \right ] \end{array} \right ]\nonumber \]
- Prueba
-
Let\(\vec{e}_{1} = \left [ \begin{array}{r} 1 \\ 0 \end{array} \right ]\) y\(\vec{e}_{2} = \left [ \begin{array}{r} 0 \\ 1 \end{array} \right ] .\) Estos identifican los vectores geométricos que apuntan a lo largo del\(x\) eje positivo y el\(y\) eje positivo como se muestra.
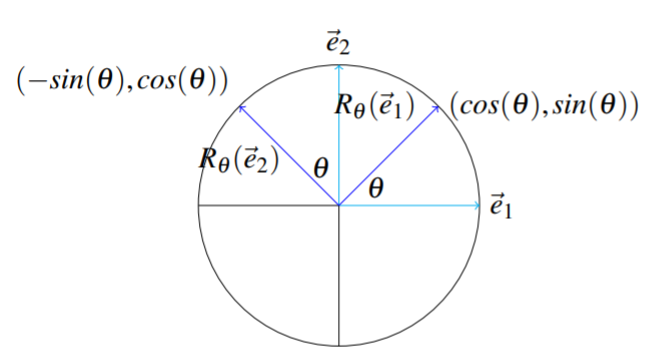
Figura\(\PageIndex{2}\) A partir del Teorema 5.2.2, necesitamos encontrar\(R_{\theta}(\vec{e}_{1})\)\(R_{\theta}(\vec{e}_{2}),\) y utilizar estos como las columnas de la matriz\(A\) de\(T\). Podemos usar\(\cos, \sin\) el ángulo\(\theta\) para encontrar las coordenadas de\(R_{\theta}(\vec{e}_{1})\) como se muestra en la imagen de arriba. Las coordenadas de\(R_{\theta}(\vec{e}_{2})\) también siguen desde la trigonometría. Así\[R_{\theta}(\vec{e}_{1})=\left [ \begin{array}{r} \cos \theta \\ \sin \theta \end{array} \right ] ,R_{\theta}(\vec{e}_{2})=\left [ \begin{array}{r} -\sin \theta \\ \cos \theta \end{array} \right ]\nonumber \] pues, a partir del Teorema 5.2.2,\[A=\left [ \begin{array}{rr} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array} \right ]\nonumber \]
También podemos demostrarlo algebraicamente sin el uso de la imagen de arriba. La definición de\(\left [ \cos \left [ \theta \right ] ,\sin \left [ \theta \right ] \right ]\) es como las coordenadas del punto de\(R_{\theta}(\vec{e}_{1})\). Ahora el punto del vector\(\vec{e}_{2}\) está exactamente\(\pi /2\) más lejos a lo largo del círculo unitario desde el punto de\(\vec{e}_{1}\), y por lo tanto después de la rotación a través de un ángulo\(y\) de\(\theta\) las coordenadas\(x\) y del punto de\(R_{\theta}(\vec{e}_{2})\) están dadas por\[\left [ x,y\right ] =\left [ \cos \left [ \theta +\pi /2\right ] ,\sin \left [ \theta +\pi /2\right ] \right ] =\left [ -\sin \theta ,\cos \theta \right ]\nonumber \]
Considera el siguiente ejemplo.
Dejar\(R_{\frac{\pi}{2}}: \mathbb{R}^2 \to \mathbb{R}^2\) denotar la rotación a través\(\pi/2\). Encuentra la matriz de\(R_{\frac{\pi}{2}}\). Entonces, encuentra\(R_{\frac{\pi}{2}} (\vec{x})\) dónde\(\vec{x} = \left [ \begin{array}{r} 1 \\ -2 \end{array} \right ]\).
Solución
Por teorema\(\PageIndex{1}\), la matriz de\(R_{\frac{\pi}{2}}\) viene dada por\[\left [ \begin{array}{rr} \cos \left [ \theta \right ] & -\sin \left [ \theta \right ] \\ \sin \left [ \theta \right ] & \cos \left [ \theta \right ] \end{array} \right ] = \left [ \begin{array}{rr} \cos \left [ \pi/2 \right ] & -\sin \left [ \pi/2 \right ] \\ \sin \left [ \pi/2 \right ] & \cos \left [ \pi/2 \right ] \end{array} \right ] = \left [ \begin{array}{rr} 0 & -1 \\ 1 & 0 \end{array} \right ]\nonumber \]
Para encontrar\(R_{\frac{\pi}{2}} (\vec{x})\), multiplicamos la matriz de\(R_{\frac{\pi}{2}}\) por\(\vec{x}\) lo siguiente\[\left [ \begin{array}{rr} 0 & -1 \\ 1 & 0 \end{array} \right ] \left [ \begin{array}{r} 1 \\ -2 \end{array} \right ] = \left [ \begin{array}{r} 2 \\ 1 \end{array} \right ]\nonumber \]
Ahora nos fijamos en un ejemplo de una transformación lineal que involucra dos ángulos.
Encontrar la matriz de la transformación lineal que se obtiene girando primero todos los vectores a través de un ángulo de\(\phi\) y luego a través de un ángulo\(\theta .\) De ahí la transformación lineal gira todos los vectores a través de un ángulo de\(\theta +\phi .\)
Solución
Vamos\(R_{\theta +\phi }\) denotar la transformación lineal que gira cada vector a través de un ángulo de\(\theta +\phi .\) Entonces para obtener primero\(R_{\theta +\phi },\) aplicamos\(R_{\phi }\) y luego\(R_{\theta }\) donde\(R_{\phi }\) está la transformación lineal que gira a través de un ángulo de\(\phi\) y\(R_{\theta }\) es la lineal transformación que gira a través de un ángulo de\(\theta\). Denotando las matrices correspondientes por\(A_{\theta +\phi }\),\(A_{\phi },\) y\(A_{\theta },\) se deduce que para cada\(\vec{u}\)\[R_{\theta +\phi }\left [\vec{u}\right ]=A_{\theta +\phi }\vec{u}=A_{\theta }A_{\phi }\vec{u} = R_{\theta }R_{\phi } \left [\vec{u}\right ]\nonumber \] Aviso el orden de las matrices aquí!
En consecuencia, debe tener\[\begin{aligned} A_{\theta +\phi } &=\left [ \begin{array}{cc} \cos \left [ \theta +\phi \right ] & -\sin \left [ \theta +\phi \right ] \\ \sin \left [ \theta +\phi \right ] & \cos \left [ \theta +\phi \right ] \end{array} \right ]\\ &=\left [ \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array} \right ] \left [ \begin{array}{cc} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{array} \right ] =A_{\theta }A_{\phi } \end{aligned}\]
Los rendimientos habituales de multiplicación matricial\[\begin{aligned} A_{\theta +\phi } &= \left [ \begin{array}{cc} \cos \left [ \theta +\phi \right ] & -\sin \left [ \theta +\phi \right ] \\ \sin \left [ \theta +\phi \right ] & \cos \left [ \theta +\phi \right ] \end{array} \right ] \\ &=\left [ \begin{array}{cc} \cos \theta \cos \phi -\sin \theta \sin \phi & -\cos \theta \sin \phi -\sin \theta \cos \phi \\ \sin \theta \cos \phi +\cos \theta \sin \phi & \cos \theta \cos \phi -\sin \theta \sin \phi \end{array} \right ] \\ &= A_{\theta }A_{\phi } \end{aligned}\]
¿Estos no te parecen familiares? Son las identidades trigonométricas habituales para la suma de dos ángulos derivados aquí utilizando conceptos de álgebra lineal.
Aquí nos hemos centrado en las rotaciones en dos dimensiones. Sin embargo, se pueden considerar rotaciones y otros conceptos geométricos en cualquier número de dimensiones. Esta es una de las principales ventajas del álgebra lineal. Se puede descomponer un procedimiento geométrico difícil en pequeños pasos, cada uno correspondiente a la multiplicación por una matriz apropiada. Luego multiplicando las matrices, puede obtener una sola matriz que le puede dar información numérica sobre los resultados de aplicar la secuencia dada de procedimientos simples.
Las transformaciones lineales que reflejan vectores a través de una línea son un segundo tipo importante de transformaciones en\(\mathbb{R}^2\). Considera el siguiente teorema.
Let\(Q_m: \mathbb{R}^2 \to \mathbb{R}^2\) Ser una transformación lineal dada por la reflexión de vectores sobre la línea\(\vec{y}=m\vec{x}\). Entonces la matriz de\(Q_m\) viene dada por\[\frac{1}{1+m^2} \left [ \begin{array}{cc} 1-m^2 & 2m \\ 2m & m^2-1 \end{array} \right ]\nonumber \]
Considera el siguiente ejemplo.
Dejar\(Q_2: \mathbb{R}^2 \to \mathbb{R}^2\) denotar reflexión sobre la línea\(\vec{y}=2\vec{x}\). Entonces\(Q_2\) es una transformación lineal. Encuentra la matriz de\(Q_2\). Entonces, encuentra\(Q_2 (\vec{x})\) dónde\(\vec{x} = \left [ \begin{array}{r} 1 \\ -2 \end{array} \right ]\).
Solución
Por teorema\(\PageIndex{2}\), la matriz de\(Q_2\) viene dada por\[\frac{1}{1+m^2} \left [ \begin{array}{cc} 1-m^2 & 2m \\ 2m & m^2-1 \end{array} \right ] = \frac{1}{1+(2)^2} \left [ \begin{array}{cc} 1-(2)^2 & 2(2) \\ 2(2) & (2)^2-1 \end{array} \right ] = \frac{1}{5} \left [ \begin{array}{rr} -3 & 8 \\ 8 & 3 \end{array} \right ]\nonumber \]
Para encontrar\(Q_2(\vec{x})\) multiplicamos\(\vec{x}\) por la matriz de\(Q_2\) lo siguiente:\[\frac{1}{5} \left [ \begin{array}{rr} -3 & 8 \\ 8 & 3 \end{array} \right ] \left [ \begin{array}{r} 1 \\ -2 \end{array} \right ] = \left [ \begin{array}{r} - \frac{19}{5} \\ \frac{2}{5} \end{array} \right ]\nonumber \]
Considere el siguiente ejemplo que incorpora una reflexión así como una rotación de vectores.
Encuentra la matriz de la transformación lineal que se obtiene girando primero todos los vectores a través de un ángulo de\(\pi /6\) y luego reflejando a través del\(x\) eje.
Solución
Por teorema\(\PageIndex{1}\), la matriz de la transformación que implica rotar a través de un ángulo de\(\pi /6\) es\[\left [ \begin{array}{rr} \cos \left [ \pi /6\right ] & -\sin \left [ \pi /6\right ] \\ \sin \left [ \pi /6\right ] & \cos \left [ \pi /6\right ] \end{array} \right ] =\left [ \begin{array}{cc} \frac{1}{2}\sqrt{3} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\sqrt{3} \end{array} \right ]\nonumber \]
Reflejar a través del\(x\) eje es la misma acción que reflejar vectores sobre la línea\(\vec{y}=m\vec{x}\) con\(m=0\). Por teorema\(\PageIndex{2}\), la matriz para la transformación que refleja todos los vectores a través del\(x\) eje es\[\frac{1}{1+m^2} \left [ \begin{array}{cc} 1-m^2 & 2m \\ 2m & m^2-1 \end{array} \right ] = \frac{1}{1+(0)^2} \left [ \begin{array}{cc} 1-(0)^2 & 2(0) \\ 2(0) & (0)^2-1 \end{array} \right ] = \left [ \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \right ]\nonumber \]
Por lo tanto, la matriz de la transformación lineal que primero gira\(\pi /6\) y luego se refleja a través del\(x\) eje viene dada por\[\left [ \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \right ] \left [ \begin{array}{rr} \frac{1}{2}\sqrt{3} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\sqrt{3} \end{array} \right ] = \ \left [ \begin{array}{rr} \frac{1}{2}\sqrt{3} & - \frac{1}{2} \\ - \frac{1}{2} & - \frac{1}{2}\sqrt{3} \end{array} \right ]\nonumber \]


