6.3: La definición del límite de una función
- Page ID
- 109440
- Explicar el límite de una función
Dado que en estos días el concepto límite es generalmente considerado como el punto de partida para el cálculo, se podría pensar que es un poco extraño que hayamos optado por hablar primero de continuidad. Pero históricamente, la definición formal de un límite vino después de la definición formal de continuidad. De alguna manera, el concepto límite fue parte de una unificación de todas las ideas de cálculo que se estudiaron previamente y, posteriormente, se convirtió en la base de todas las ideas en cálculo. Por esta razón es lógico convertirlo en el primer tema tratado en un curso de cálculo.
Sin duda, los límites siempre estaban al acecho en el fondo. En sus intentos de justificar sus cálculos, Newton utilizó lo que él llamó su doctrina de “Ratios definitivos. ” Específicamente la relación
\[\dfrac{(x+h)^2 - x^2}{h} = \dfrac{2xh+h^2}{h} = 2x + h\]
se convierte en la relación\(2x\) final en el último instante del tiempo antes de que\(h\) - una “cantidad evanescente” - se desvanezca. De igual manera Leibniz, los diferenciales “infinitamente pequeños”\(dx\) y\(dy\) pueden verse como un intento de acercarse “arbitrariamente” a\(x\) y\(y\), respectivamente. Esta es la idea en el centro del cálculo: acercarse arbitrariamente, digamos,\(x\) sin llegar realmente a él.
Como vimos en el Capítulo 3, Lagrange intentó evitar todo el tema de la “cercanía arbitraria”, tanto en las formas límite como en las diferenciales cuando, en 1797, intentó fundar el cálculo en series infinitas.
Si bien los esfuerzos de Lagrange fracasaron, sentaron las bases para que Cauchy proporcionara una definición de derivado que a su vez se basó en su formulación precisa de un límite. Considere el siguiente ejemplo: para determinar la pendiente de la línea tangente (derivada) de\(f(x) = \sin x\) at\(x = 0\). Consideramos la gráfica del cociente de diferencia\(D(x) = \dfrac{\sin x}{x}\).
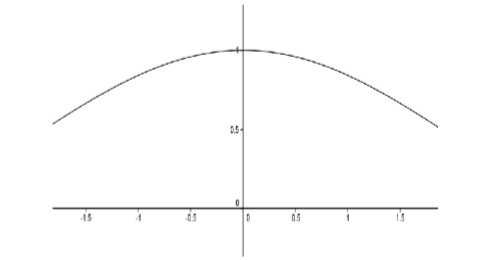
Figura\(\PageIndex{1}\): Pendiente de la línea tangente (derivada) de\(f(x) = \sin x\).
De la gráfica, parece que\(D(0) = 1\) pero hay que tener cuidado. \(D(0)\)¡ni siquiera existe! De alguna manera debemos transmitir la idea de que\(D(x)\) se acercará\(1\) como\(x\) enfoques\(0\), aunque la función no esté definida en\(0\). La idea de Cauchy era que el límite de\(D(x)\) sería igual\(1\) porque podemos hacer\(D(x)\) diferir de\(1\) por lo poco que deseemos.
Karl Weierstrass precisó estas ideas en sus conferencias sobre análisis en la Universidad de Berlín (1859-60) y nos proporcionó nuestra formulación moderna.
Decimos\(\displaystyle \lim_{x \to a} f(x) = L\) siempre que para cada uno\(ε > 0\), exista\(δ > 0\) tal que si\(0 < |x - a| < δ\) entonces\(|f(x) - L| < ε\).
Antes de ahondar en esto, notemos que es muy similar a la definición de la continuidad de\(f(x)\) at\(x = a\). De hecho podemos ver fácilmente que\(f\) es continuo en\(x = a\) si y solo si\( \displaystyle \lim_{x \to a} f(x) = f(a)\).
Hay dos diferencias entre esta definición y la definición de continuidad y están relacionadas. El primero es que sustituimos el valor\(f(a)\) por\(L\). Esto se debe a que la función puede no estar definida en\(a\). En cierto sentido el valor limitante\(L\) es el valor que\(f\) tendría si estuviera definido y continuo en\(a\). El segundo es que hemos reemplazado
\[|x - a| < δ\]
con
\[0 < |x - a| < δ\]
Nuevamente, como\(f\) no hace falta definirse en\(a\), ni siquiera vamos a considerar qué pasa cuando\(x = a\). Este es el único propósito de este cambio.
Al igual que con la definición del límite de una secuencia, esta definición no determina qué\(L\) es, solo verifica que tu conjetura para el valor del límite sea correcta.
Finalmente, algunos comentarios sobre las diferencias y similitudes entre este límite y el límite de una secuencia están en orden, si no por otra razón que porque usamos la misma notación (\( \displaystyle \lim\)) para ambos.
Cuando estábamos trabajando con secuencias en el Capítulo 4 y escribimos cosas como si\( \displaystyle \lim_{n \to \infty } a_n\) estuviéramos pensando\(n\) como un entero que se hacía cada vez más grande. Para decirlo más matemáticamente, el parámetro limit\(n\) se tomó del conjunto de enteros positivos, o\(n ∈ \mathbb{N}\).
Tanto para la continuidad como para el límite de una función escribimos cosas como\( \displaystyle \lim_{x \to a} f(x)\) y pensamos en ellas\(x\) como una variable que se acerca arbitrariamente al número\(a\). Nuevamente, para ser más matemáticos en nuestro lenguaje diríamos que el parámetro limit\(x\) se toma del... Bueno, en realidad, esto es interesante, ¿no? ¿Tenemos que tomar\(x\) de\(\mathbb{Q}\) o de\(\mathbb{R}\)? El requisito en ambos casos es simplemente que seamos capaces de elegir\(x\) arbitrariamente cerca de a. del Teorema 1.1.2 del Capítulo 1 vemos que esto es posible ya sea\(x\) racional o no, por lo que parece que o bien va a funcionar. Esto lleva a la conclusión de sondeo pardoxico de que no necesitamos un continuum (\(\mathbb{R}\)) para tener continuidad. Esto parece extraño.
Antes de mirar el ejemplo anterior, veamos algunos ejemplos algebraicos para ver la definición en uso.
Considera la función\(D(x) = \dfrac{x^2 -1}{x-1}, x\neq 1\). Probablemente reconozcas esto como el cociente de diferencia utilizado para calcular la derivada de\(f(x) = x^2\) at\(x = 1\), así que sospechamos fuertemente que\( \displaystyle \lim_{x \to 1}\dfrac{x^2 -1}{x-1} = 2\). Así como cuando estábamos tratando con límites de secuencias, deberíamos poder usar la definición para verificar esto. Y como antes, comenzaremos con algunos recortes.
Scrapwork:
Vamos\(ε > 0\). Deseamos encontrar\(δ > 0\) tal que si\(0 < |x - 1| < δ\) entonces\(\left |\dfrac{x^2 -1}{x-1} - 2 \right | < \varepsilon\). Con esto en mente, realizamos los siguientes cálculos
\[ \begin{align*} \left |\dfrac{x^2 -1}{x-1} - 2 \right | &= \left | (x+1) - 2 \right | \\[4pt] &= \left | x - 1 \right | \end{align*}\]
Ahora tenemos un control sobre\(δ\) eso va a funcionar en la definición y vamos a dar la prueba formal de que
\[\lim_{x \to 1}\dfrac{x^2 -1}{x-1} = 2 \nonumber\]
Fin de Scrapwork.
Prueba:
Dejar\(ε > 0\) y dejar\(δ = ε\). Si\(0 < |x - 1| < δ\), entonces
\[ \begin{align*} \left |\dfrac{x^2 -1}{x-1} - 2 \right | &= \left | (x+1) - 2 \right | \\[4pt] &= \left | x - 1 \right | < \delta = \varepsilon \end{align*}\]
Al igual que en nuestro trabajo anterior con secuencias y continuidad, notemos que el scrapwork no forma parte de la prueba formal (aunque fue necesario determinar una apropiada\(δ\)). También, aviso que\(0 < |x - 1|\) realmente no se utilizó excepto para asegurar eso\(x \neq 1\).
Utilice la definición de un límite para verificar que
\[ \displaystyle \lim_{x \to a}\dfrac{x^2 - a^2}{x-a} = 2a.\]
Utilice la definición de un límite para verificar cada uno de los siguientes límites.
- \(\displaystyle \lim_{x \to 1}\dfrac{x^3 - 1}{x-1} = 3\)
- \(\displaystyle \lim_{x \to 1} \dfrac{\sqrt{x}-1}{x-1} = \dfrac{1}{2}\)
- Insinuar a
-
\[\begin{align*} \left |\dfrac{x^3 - 1}{x-1} - 3 \right | &= \left | x^2 + x + 1 - 3 \right |\\ &\leq \left | x^2 - 1 \right | + \left | x - 1 \right |\\ &= \left | (x-1+1)^2 - 1 \right | + \left | x - 1 \right |\\ &= \left | (x-1)^2 +2(x-1) \right | + \left | x - 1 \right |\\ &\leq \left | x - 1 \right |^2 + 3\left | x - 1 \right | \end{align*}\]
- Pista b
-
\[\begin{align*} \left | \dfrac{\sqrt{x}-1}{x-1} - \dfrac{1}{2} \right | &= \left |\dfrac{1}{\sqrt{x}+1} - \dfrac{1}{2} \right |\\ &= \left | \dfrac{2-(\sqrt{x}+1)}{2(\sqrt{x})+1} \right |\\ &= \left | \dfrac{1-x}{2(1+\sqrt{x})^2} \right |\\ &\leq \dfrac{1}{2}\left | x-1 \right | \end{align*}\]
Volvamos al problema original: para demostrarlo\( \displaystyle \lim_{x \to 0} \dfrac{\sin x}{x} = 1\).
Si bien es rigurosa, nuestra definición de continuidad es bastante engorrosa. Realmente necesitamos desarrollar algunas herramientas que podamos usar para mostrar la continuidad rigurosamente sin tener que referirnos directamente a la definición. Ya hemos visto en el Teorema 6.2.1 una manera de hacer esto. Aquí hay otro. La clave es la observación que hicimos después de la definición de un límite:
\[f \text{ is continuous at } x = a \text{ if and only if }\lim_{x \to a} f(x) = f(a)\]
Leer de otra manera, podríamos decir que\( \displaystyle \lim_{x \to a} f(x) = L\) siempre que si redefinimos\(f(a) = L\) (o definimos\(f(a) = L\) en el caso donde no\(f(a)\) se define) entonces\(f\) se vuelve continuo en\(a\). Esto nos permite utilizar toda la maquinaria que probamos sobre funciones continuas y límites de secuencias.
Por ejemplo, el siguiente corolario al Teorema 6.2.1 viene virtualmente de forma gratuita una vez que hemos hecho la observación anterior.
\( \displaystyle \lim_{x \to a} f(x) = L\)si y solo si\(f\) satisface la siguiente propiedad:
\[\forall \text{ sequences }(x_n),x_n\neq a, \text{ if }\lim_{x \to \infty } x_n = a \text{ then } \lim_{x \to \infty } f(x_n) = L\]
Armados con esto, podemos probar los siguientes teoremas de límite familiares a partir del cálculo.
Supongamos\( \displaystyle \lim_{x \to a} f(x) = L\) y\( \displaystyle \lim_{x \to a} g(x) = M\), entonces
- \(\displaystyle \lim_{x \to a} (f(x) + g(x)) = L + M\)
- \(\displaystyle \lim_{x \to a} (f(x) \cdot g(x)) = L \cdot M\)
- \(\displaystyle \lim_{x \to a} \left ( \dfrac{f(x)}{g(x)} \right ) = \dfrac{L}{M}\)siempre\(M \neq 0\) y\(g(x) \neq 0\), por\(x\) suficientemente cerca de\(a\) (pero no igual a\(a\)).
Demostraremos la parte (a) para darle una idea de esto y permitirle probar las partes (b) y (c).
Let (\(x_n\)) ser una secuencia tal que\(x_n \neq a\) y\(\displaystyle \lim_{n \to \infty }x_n = a\). Desde\(\displaystyle \lim_{x \to a} f(x) = L\) y\(\displaystyle \lim_{x \to a} g(x) = M\) vemos que\(\displaystyle \lim_{n \to \infty } f(x_n) = L\) y\( \displaystyle \lim_{n \to \infty } g(x_n) = M\). Por Teorema 4.2.1 del Capítulo 4, tenemos\(\displaystyle \lim_{n \to \infty } f(x_n) + g(x_n) = L + M\). Desde {\(x_n\)} fue una secuencia arbitraria con\(x_n \neq a\) y\( \displaystyle \lim_{n \to \infty }x_n = a\) tenemos
\[\lim_{x \to a} f(x) + g(x) = L + M.\nonumber \]
Demostrar las partes (b) y (c) del Teorema\(\PageIndex{1}\).
Más en línea con nuestras necesidades actuales, tenemos una reformulación del Teorema de Squeeze.
Supongamos\(f(x) ≤ g(x) ≤ h(x)\), para\(x\) suficientemente cerca de\(a\) (pero no igual a\(a\)). Si
\[\lim_{x \to a} f(x) = L = \lim_{x \to a} h(x)\]
luego también
\[\lim_{x \to a} g(x) = L.\]
Demostrar teorema\(\PageIndex{2}\).
- Pista
-
Utilice el Teorema de Squeeze para las secuencias (Teorema 4.2.4) del Capítulo 4.
Volviendo a\( \displaystyle \lim_{x \to 0} \dfrac{\sin x}{x}\) veremos que el Teorema de Squeeze es justo lo que necesitamos. Primero notamos que ya que\(D(x) = \dfrac{\sin x}{x}\) es una función par, solo necesitamos enfocarnos\(x > 0\) en nuestras desigualdades. Considera el círculo unitario.
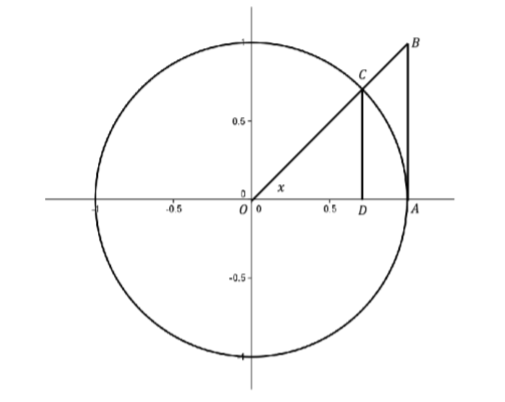
Figura\(\PageIndex{2}\): El círculo de la Unidad.
Usa el hecho de que\(\text{area}(∆OAC) < \text{area}(sector OAC) < \text{area}(∆OAB)\) para demostrar que si\(0 < x < \dfrac{π}{2}\), entonces\(\cos x < \dfrac{\sin x}{x} < 1\). Usa el hecho de que todas estas funciones son incluso para extender la desigualdad para\(-\dfrac{π}{2} < x < 0\) y usar el Teorema de Squeeze para mostrar\( \displaystyle \lim_{x \to 0} \dfrac{\sin x}{x} = 1\).

