6.4: El Derivado - Una ocurrencia de último momento
- Page ID
- 109414
- Explicar la derivada
No, el derivado no es realmente una idea de último momento. Junto con la integral es, de hecho, uno de los objetos matemáticos más potentes y útiles jamás ideados y hemos estado trabajando muy duro para proporcionar una base sólida y rigurosa para ello. En ese sentido es un foco primordial de nuestras investigaciones.
Por otro lado, ahora que hemos construido toda la maquinaria que necesitamos para definir y explorar el concepto de la derivada, aparecerá bastante peatonal junto a ideas como la convergencia de series de poder, series de Fourier, y las extrañas propiedades de\(\mathbb{Q}\) y\(\mathbb{R}\).
Pasaste un semestre entero aprendiendo sobre las propiedades del derivado y cómo utilizarlas para explorar las propiedades de las funciones así que no vamos a repetir ese esfuerzo aquí. En cambio, la definiremos formalmente en términos de las ideas y técnicas que hemos desarrollado hasta ahora.
Dada una función\(f(x)\) definida en un intervalo\((a,b)\) definimos
\[f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\]
Hay algunos hechos bastante obvios sobre esta definición que, sin embargo, vale la pena notar explícitamente:
- La derivada se define en un punto. Si se define en cada punto en un intervalo\((a,b)\) entonces decimos que la derivada existe en cada punto del intervalo.
- Dado que se define en un punto es al menos teóricamente posible que una función sea diferenciable en un solo punto en todo su dominio.
- Dado que se define como un límite y no todos los límites existen, las funciones no son necesariamente diferenciables.
- Ya que se define como un límite, aplica el Corolario 6.3.1. Es decir,\(f'(x)\) existe si y solo si\(∀\) secuencias (\(h_n\)),\(h_n \neq 0\), si lim n→∞ hn = 0 entonces\[f'(x) = \lim_{n \to \infty }\frac{f(x+h_n)-f(x)}{h_n}\] Dado que\(\lim_{n \to \infty }h_n = 0\) esto también podría escribirse como\[f'(x) = \lim_{h_n \to 0}\frac{f(x+h_n)-f(x)}{h_n}\]
Si\(f\) es diferenciable en un punto\(c\) entonces\(f\) es continuo en\(c\) también.
Demostrar teorema\(\PageIndex{1}\).
Como mencionamos, la derivada es una herramienta matemática extraordinariamente útil pero no es nuestra intención aprender a usarla aquí. Nuestro propósito aquí es definirlo rigurosamente (hecho) y demostrar que nuestra definición formal de hecho recupera las propiedades útiles que llegaste a conocer y amar en tu curso de cálculo.
La primera propiedad de este tipo se conoce como Teorema de Fermat.
Supongamos que\(f\) es diferenciable en algún intervalo\((a,b)\) que contenga\(c\). Si\(f(c) ≥ f(x)\) por cada\(x\) en\((a,b)\), entonces\(f'(c) = 0\).
Prueba:
Ya que\(f'(c)\) existe sabemos que si\(\left ( h_n \right )_{n=1}^{\infty }\) converge a cero entonces la secuencia\(a_n = \frac{f(c+h_n)-f(c)}{h_n}\) converge a\(f'(c)\). La prueba consiste en demostrar eso\(f'(c) ≤ 0\) y aquello\(f'(c) ≥ 0\) de lo que concluimos eso\(f'(c) = 0\). Sólo mostraremos la primera parte. El segundo se deja como ejercicio.
Reclamación:\(f'(c) ≤ 0\).
Deje\(n_0\) que sea suficientemente grande eso\(\frac{1}{n_0} < b -c\) y tome\((h_n) = \left ( \frac{1}{n} \right )_{n=n_0}^{\infty }\). Entonces\(f\left ( c + \frac{1}{n} \right ) - f(c) \leq 0\) y\(\frac{1}{n} > 0\), para que
\[\frac{f(c+h_n)-f(c)}{h_n} \leq 0, \forall_n = n_0, n_0+1, \cdots\]
Por lo tanto
\[f'(c) = \lim_{h_n \to 0}\frac{f(c+h_n)-f(c)}{h_n} \leq 0\]
Demostrar eso\(f'(c) ≥ 0\) y concluir que\(f'(c) = 0\).
Demuestre que si\(f(c) ≤ f(x)\) para todos\(x\) en algún intervalo\((a,b)\) entonces\(f'(c) = 0\) también.
Muchas de las propiedades más importantes de la derivada se derivan de lo que se llama el Teorema del Valor Medio (MVT) que ahora declaramos.
Supongamos que\(f'\) existe para todos\(x ∈ (a,b)\) y\(f\) es continuo en\([a,b]\). Entonces hay un número real\(c ∈ (a,b)\) tal que
\[f'(c) = \frac{f(b)-f(a)}{b-a}\]
No obstante, sería difícil probar el MVT en estos momentos. Por lo que primero declararemos y probaremos el Teorema de Rolle, que puede verse como un caso especial del MVT. La prueba del MVT seguirá entonces fácilmente.
Michel Rolle declaró por primera vez el siguiente teorema en 1691. Dada esta fecha y la naturaleza del teorema sería razonable suponer que Rolle fue uno de los primeros desarrolladores del cálculo pero esto no es así. De hecho, Rolle despreciaba tanto las versiones del cálculo de Newton como de Leibniz, una vez ridiculizándolas como una colección de “ingeniosas falacias. ” Es un poco irónico que su teorema sea tan fundamental para el desarrollo moderno del cálculo que ridiculizó.
Supongamos que\(f'\) existe para cada\(x ∈ (a,b)\),\(f\) es continuo en\([a,b]\), y
\[f(a) = f(b)\]
Entonces hay un número real\(c ∈ (a,b)\) tal que
\[f'(c) = 0\]
Prueba:
Ya que\(f\) es continuo en\([a,b]\) vemos, por el Teorema del Valor Extremo, que\(f\) tiene tanto un máximo como un mínimo on\([a,b]\). Denotar el máximo por\(M\) y el mínimo por\(m\). Hay varios casos:
Caso 1:
\(f(a) = f(b) = M = m\). En este caso\(f(x)\) es constante (¿por qué?). Por lo tanto\(f'(x) = 0\) para cada\(x ∈ (a,b)\).
Caso 2:
\(f(a) = f(b) = M \neq m\). En este caso hay un número real\(c ∈ (a,b)\) tal que\(f(c)\) es un mínimo local. Por el teorema de Fermat,\(f'(c) = 0\).
Caso 3:
\(f(a) = f(b) = m \neq M\). En este caso hay un número real\(c ∈ (a,b)\) tal que\(f(c)\) es un máximo local. Por el teorema de Fermat,\(f'(c) = 0\).
Caso 4:
\(f(a) = f(b)\)no es ni un máximo ni un mínimo. En este caso hay un número real\(c_1 ∈ (a,b)\) tal que\(f(c_1)\) es un máximo local, y un número real\(c_2 ∈ (a,b)\) tal que\(f(c_2)\) es un mínimo local. Por el teorema de Fermat,\(f'(c_1) = f'(c_2) = 0\).
Con el Teorema de Rolle en la mano podemos probar el MVT que es realmente un corolario del Teorema de Rolle o, más precisamente, es una generalización del Teorema de Rolle. Para demostrarlo solo necesitamos encontrar la función correcta a la que aplicar el Teorema de Rolle. En la siguiente figura se\(\PageIndex{1}\) muestra una función\(f(x)\),, cortada por una línea secante,\(L(x)\), de\((a,f(a))\) a\((b,f(b))\).
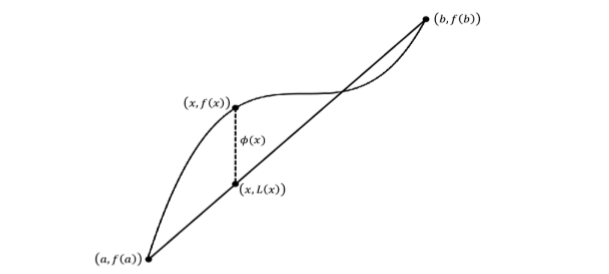
Figura\(\PageIndex{1}\): Aplicando el Teorema de Rolle.
La diferencia vertical de\(f(x)\) a la línea secante, indicada por\(φ(x)\) en la figura debe hacer el truco. Lo tomas de ahí.
Demostrar el Teorema del Valor Medio.
El Teorema del Valor Medio es extraordinariamente útil. Casi todas las propiedades del derivado que utilizaste en el cálculo siguen más o menos fácilmente de él. Por ejemplo lo siguiente es cierto.
Si\(f'(x) > 0\) por cada\(x\) en el intervalo\((a,b)\) entonces para cada\(c,d ∈ (a,b)\) donde\(d > c\) tenemos
\[f(d) > f(c)\]
Es decir,\(f\) está aumentando en\((a,b)\).
Prueba:
Supongamos\(c\) y\(d\) son como se describe en el corolario. Entonces por el Teorema del Valor Medio hay algún número, digamos\(α ∈ (c,d) ⊆ (a,b)\) tal que
\[f'(\alpha ) = \frac{f(d)-f(c)}{d-c}\]
Desde\(f'(α) > 0\) y\(d - c > 0\) tenemos\(f(d) - f(c) > 0\), o\(f(d) > f(c)\).
Mostrar que si\(f'(x) < 0\) para cada\(x\) en el intervalo\((a,b)\) entonces\(f\) está disminuyendo en\((a,b)\).
Supongamos que\(f\) es diferenciable en algún intervalo\((a,b)\),\(f'\) es continuo encendido\((a,b)\), y eso\(f'(c) > 0\) para algunos\(c ∈ (a,b)\). Entonces hay un intervalo,\(I ⊂ (a,b)\), que contiene\(c\) tal que para cada\(x,y\) en\(I\) donde\(x ≥ y, f(x) ≥ f(y)\).
Demostrar Corolario\(\PageIndex{2}\).
Mostrar que si\(f\) es diferenciable en algún intervalo\((a,b)\) y que\(f'(c) < 0\) para algunos\(c ∈ (a,b)\) entonces hay un intervalo,\(I ⊂ (a,b)\), conteniendo\(c\) tal que para cada\(x,y\) en\(I\) donde\(x ≤ y, f(x) ≤ f(y)\).

