7.1: Completitud del sistema de números reales

Última actualización
Guardar como PDF

Page ID: 109525

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Explicar el sistema de números reales

Recordemos que al derivar las formas Lagrange y Cauchy del resto para la serie Taylor, se utilizó el Teorema del Valor Extremo (EVT) y el Teorema del Valor Intermedio (IVT). En el capítulo 6, se produjo una definición analítica de continuidad que podemos utilizar para probar estos teoremas. Para proporcionar el resto de las herramientas necesarias necesitamos para explorar la composición del sistema de números reales. Para ilustrar lo que queremos decir, supongamos que solo usamos el sistema numérico racional. Todavía podríamos usar nuestra definición de continuidad y aún podríamos considerar funciones continuas como$f(x) = x^2$. Observe que$2$ es un valor que se encuentra entre$f(1) = 1$ y$f(2) = 4$.

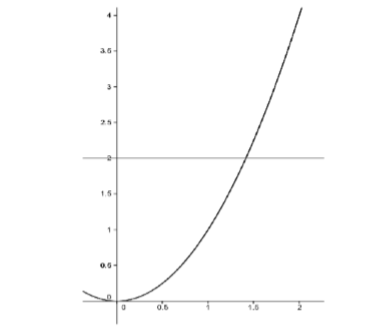
$higo 7.1.1.png$

Figura$\PageIndex{1}$: Gráfica de la función$f(x) = x^2$.

El IVT dice que en algún lugar entre$1$ y$2$,$f$ debe asumir el valor$2$. Es decir, debe existir algún número$c ∈ [1,2]$ tal que$f(c) = 2$. Podrías decir: “¡Gran cosa! Todo el mundo sabe$c = \sqrt{2}$ obras. ”

No obstante, sólo estamos trabajando con números racionales y no$\sqrt{2}$ es racional. Como vimos en el Capítulo 1, el sistema numérico racional tiene agujeros en él, mientras que el sistema numérico real no. De nuevo, “¡Gran cosa! Digamos que el sistema de números reales contiene raíces (cuadradas). ”

Esto suena razonable y en realidad funciona para raíces cuadradas, pero considera la función$f(x) = x - \cos x$. Sabemos que esta es una función continua. También sabemos que$f(0) = -1$ y$f(\frac{π}{2}) = \frac{π}{2}$. De acuerdo con la IVT, debería haber algún número$c ∈ [0, \frac{π}{2}]$, dónde$f(c) = 0$. A continuación se muestra la gráfica.

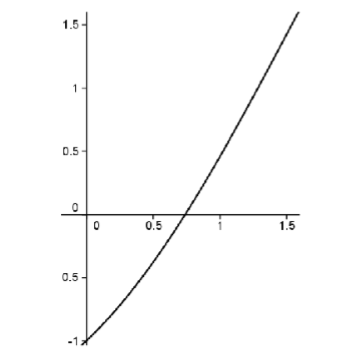
$higo 7.1.2.png$

Figura$\PageIndex{2}$: Gráfica de$f(x) = x - \cos x$.

La situación no es tan transparente como antes. ¿Cuál sería este misterioso$c$ donde la curva cruza el$x$ eje? De alguna manera necesitamos transmitir la idea de que el sistema de números reales es un continuo. Es decir, no tiene “agujeros” en él.

¿Qué tal esto? ¿Por qué no decimos simplemente que no tiene agujeros? ¡A veces la respuesta simple funciona mejor! Pero no en este caso. ¿Cómo vamos a formular una prueba rigurosa basada en esta afirmación? Al igual que con la convergencia y la continuidad, lo que necesitamos es una forma rigurosa de transmitir esta idea de que el sistema de números reales no tiene agujeros, que está completo.

Veremos que existen varias formas diferentes, pero equivalentes, de transmitir esta noción de integridad. Exploraremos algunas de ellas en este capítulo. Por ahora adoptamos lo siguiente como nuestro Axioma de Completeza para el sistema de números reales.

Propiedad Intervalo Anidado del Sistema de Número Real (NIP)

Supongamos que tenemos dos secuencias de números reales ($x_n$) y ($y_n$) que satisfacen las siguientes condiciones:

$x_1 ≤ x_2 ≤ x_3 ≤ ...$[($x_n$) no es decreciente]
$y_1 ≥ y_2 ≥ y_3 ≥ ...$[($y_n$) no aumenta]
$∀ n, x_n ≤ y_n $
$\lim_{n \to \infty } (y_n - x_n) = 0$

Entonces existe un número único$c$ tal que$x_n ≤ c ≤ y_n$ para todos$n$. Geométricamente, tenemos la siguiente situación.

$higo 7.1.3.png$

Figura$\PageIndex{3}$: Representación de líneas numéricas de$x_n$ y$y_n$.

Observe que tenemos dos secuencias ($x_n$) y ($y_n$), una creciente (realmente no decreciente) y otra decreciente (no creciente). Estas secuencias no se pasan entre sí. De hecho, es cierto lo siguiente:

Ejercicio$\PageIndex{1}$

Let ($x_n$), ($y_n$) sean secuencias como en el NIP. Demuéstralo para todos$n$,$m ∈N$,$x_n ≤ y_m$.

También se están uniendo en el sentido de que$\lim_{n \to \infty } (y_n - x_n) = 0$. El NIP dice que en este caso hay un número real único$c$ en medio de todo esto [$x_n ≤ c ≤ y_n$para todos$n$].

$higo 7.1.4.png$

Figura$\PageIndex{4}$: Resentación de repetición de línea numérica de$c$.

Si no hubiera tal$c$ entonces habría un agujero donde se juntan estas dos secuencias. El NIP garantiza que no existe tal agujero. No necesitamos probarlo ya que un axioma es, por definición, una verdad autoevidente. Estamos tomando con fe que el sistema de números reales obedece a esta ley. El siguiente problema muestra que la propiedad de integridad distingue el sistema de números reales del sistema numérico racional.

Ejercicio$\PageIndex{2}$

Encontrar dos secuencias de números racionales ($x_n$) y ($y_n$) que satisfagan las propiedades 1-4 del NIP y tal que no haya un número racional que$c$ satisfaga la conclusión del NIP.

Pista: Considera la expansión decimal de un número irracional.

Encontrar dos secuencias de números racionales ($x_n$) y ($y_n$) que satisfagan las propiedades 1-4 del NIP y tal que haya un número racional que$c$ satisfaga la conclusión del NIP.

Puede que el nombre Propiedad de intervalo anidado sea algo curioso. Una forma de pensar sobre esta propiedad es considerar que tenemos una secuencia de “intervalos cerrados anidados”$[x_1,y_1] ⊇ [x_2,y_2] ⊇ [x_3,y_3] ⊇···$ cuyas longitudes$y_n - x_n$ se están “reduciendo a$0$. ” La conclusión es que la intersección de estos intervalos no es vacía y, de hecho, consiste en un solo punto. Es decir,$\bigcap _{n=1}^{\infty } [x_n, y_n] = \{c\}$.

teorema$\PageIndex{1}$

Supongamos que tenemos dos secuencias ($x_n$) y ($y_n$) que satisfacen todos los supuestos de la Propiedad Intervalo Anidado. Si$c$ es el número único tal que$x_n ≤ c ≤ y_n$ para todos$n$, entonces$\lim_{n \to \infty } x_n = c$ y$\lim_{n \to \infty } y_n = c$.

Ejercicio$\PageIndex{3}$

Demostrar teorema$\PageIndex{1}$.

Para ilustrar la idea de que el NIP “tapona los agujeros” en la línea real, probaremos la existencia de raíces cuadradas de números reales no negativos.

teorema$\PageIndex{2}$

Supongamos$a ∈ \mathbb{R}$,$a ≥ 0$. Existe un número real$c ≥ 0$ tal que$c^2 = a$.

Observe que no podemos simplemente decir “Vamos”$c = \sqrt{a}$, ya que la idea es mostrar que esta raíz cuadrada existe. De hecho, a lo largo de esta prueba, realmente no podemos usar un símbolo de raíz cuadrada ya que aún no hemos demostrado que existan (raíces cuadradas). Daremos la idea detrás de la prueba ya que ilustra cómo se usa el NIP.

Croquis de Prueba:

Nuestra estrategia es construir dos secuencias que se “estrechen” en el número$c$ que buscamos. Con eso en mente, necesitamos encontrar un número$x_1$ tal que$x^2_1 ≤ a$ y un número$y_1$ tal que$y^2_1 ≥ a$. (Recuerda que no podemos decir$\sqrt{x_1}$ o$\sqrt{y_1}$.) Hay muchas posibilidades, pero ¿qué tal$x_1 = 0$ y$y_1 = a + 1$? Se puede comprobar que estos satisfarán$x^2_1 ≤ a ≤ y^2_1$. Además$x_1 ≤ y_1$. Este es el punto de partida.

La técnica que emplearemos a menudo se denomina técnica de bisección, y es una forma útil de prepararnos para aplicar el NIP. Dejar$m_1$ ser el punto medio del intervalo$[x_1,y_1]$. Entonces o tenemos$m^2_1 ≤ a$ o$m^2_1 ≥ a$. En el caso$m^2_1 ≤ a$, realmente queremos$m_1$ tomar el lugar de$x_1$ ya que es más grande que$x_1$, pero aún representa una subestimación para lo que sería la raíz cuadrada de$a$. Este pensamiento suscita el siguiente movimiento. Si$m^2_1 ≤ a$, vamos a remarcar las cosas dejando$x_2 = m_1$ y$y_2 = y_1$. La situación se ve así en la recta numérica.

$higo 7.1.5.png$

Figura$\PageIndex{5}$: Representación de líneas numéricas.

En el otro caso donde$a ≤ m^2_1$, vamos a remarcar las cosas dejando$x_2 = x_1$ y$y_2 = m_1$. La situación se ve así en la recta numérica.

$higo 7.1.6.png$

Figura$\PageIndex{6}$: Representación de líneas numéricas.

En cualquier caso, hemos reducido la longitud del intervalo donde se encuentra la raíz cuadrada a la mitad del tamaño que tenía antes. Declarado en términos más específicos, en cualquier caso tenemos los mismos resultados:

\[x_1 ≤ x_2 ≤ y_2 ≤ y_1;\; x^2_1 ≤ a ≤ y^2_1;\; x^2_2 ≤ a ≤ y^2_2\]

\[y_2 - x_2 = \frac{1}{2}(y_1 - x_1)\]

Ahora jugamos el mismo juego, pero en cambio empezamos con el intervalo$[x_2,y_2]$. Dejar$m_2$ ser el punto medio de$[x_2,y_2]$. Entonces tenemos$m^2_2 ≤ a$ o$m^2_2 ≥ a$. Si$m^2_2 ≤ a$, reetiquetamos$x_3 = m_2$ y$y_3 = y_2$. Si$a ≤ m^2_2$, reetiquetamos$x_3 = x_2$ y$y_3 = m_2$. En cualquier caso, terminamos con

\[x_1 \leq x_2 \leq x_3 \leq y_3 \leq y_2 \leq y_1;\; x^2_1 \leq a \leq y^2_1;\; x^2_2 \leq a \leq y^2_2;\; x^2_3 \leq a \leq y^2_3\]

\[y_3 - x_3 = \frac{1}{2}(y_2 - x_2) = \frac{1}{2^2}(y_1 - x_1)\]

Continuando de esta manera, produciremos dos secuencias, ($x_n$) y ($y_n$) satisfaciendo las siguientes condiciones:

$x_1 ≤ x-2 ≤ x_3 ≤ ... $
$y_1 ≥ y_2 ≥ y_3 ≥ ... $
$∀ n$,$x_n ≤ y_n$
$\lim_{n \to \infty } (y_n - x_n) = \lim_{n \to \infty } \frac{1}{2^{n-1}}(y_1 - x_1) = 0$
Estas secuencias también satisfacen la siguiente propiedad:\[∀ n,\; x^2_n ≤ a ≤ y^2_n\]

Las propiedades 1-4 nos dicen que ($x_n$) y ($y_n$) satisfacen todas las condiciones del NIP, por lo que podemos concluir que debe existir un número real$c$ tal que$x_n ≤ c ≤ y_n$ para todos$n$. En este punto, debería poder utilizar la propiedad 5. para mostrar eso$c^2 = a$ como se desee.

Ejercicio$\PageIndex{4}$

Convertir el esquema anterior en una prueba formal del Teorema$\PageIndex{2}$.

El método de bisección que empleamos en la prueba de Teorema$\PageIndex{2}$ es bastante típico de cómo usaremos el NIP, ya que tomar puntos medios asegura que crearemos una secuencia de “intervalos anidados. ” Emplearemos esta estrategia en las pruebas de la IVT y EVT. Decidir cómo remarcar los puntos finales de nuestros intervalos estará determinado por lo que queremos hacer con estas dos secuencias de números reales. Esto generalmente conducirá a una quinta propiedad, lo que será crucial para demostrar que la c garantizada por el NIP hace lo que queremos que haga. Específicamente, en el ejemplo anterior, siempre quisimos que nuestro candidato$\sqrt{a}$ para estuviera en el intervalo$[x_n,y_n]$. Esta elección juiciosa llevó a la propiedad extra 5:$∀ n$,$x^2_n ≤ a ≤ y^2_n$. Al aplicar el NIP para acreditar la IVT y EVT, encontraremos que las propiedades 1-4 permanecerán igual. Propiedad 5 es lo que va a cambiar en base a la propiedad que$c$ queremos tener.

Antes de abordar el IVT y EVT, usemos el NIP para abordar una pregunta interesante sobre la Serie Armónica. Recordemos que la Serie Armónica$1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots$,, crece sin ataduras, es decir,$\sum_{n=1}^{\infty } \frac{1}{n} = \infty$. La pregunta es ¿qué tan lentamente crece esta serie? Por ejemplo, ¿cuántos términos tomaría antes de que la serie supere$100$? $1000$? $10000$? Leonhard Euler decidió abordar este problema de la siguiente manera. Euler decidió considerar el$\lim_{n \to \infty }\left (\left ( 1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \right ) - \ln (n+1) \right )$. Este límite se llama constante de Euler y se denota por$γ$. Esto dice que para$n$ grandes, tenemos$1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \approx \ln (n+1) + \gamma$. Si pudiéramos aproximarnos$γ$, entonces podríamos reemplazar la desigualdad$1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \geq 100$ con la igualdad más manejable$\ln ( n + 1) + γ ≥ 0$ y resolverla$n$ en esto. Esto debería decirnos aproximadamente cuántos términos necesitarían agregarse en la Serie Armónica para superarlos$100$. Aproximarse$γ$ con una computadora no es tan malo. Podríamos hacer$n$ lo más grande que deseemos en$\left (1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \right ) - \ln (1+n)$ hacer aproximaciones más cercanas para$γ$. El verdadero problema es, ¿CÓMO SABEMOS ESO?

\[\lim_{n \to \infty }\left (\left (1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \right ) - \ln (n+1) \right )\]

EN REALIDAD EXISTE?

Quizás quieras decir que obviamente debería, pero señalemos que a partir de la impresión de este libro (2013), ni siquiera se sabe si$γ$ es racional o irracional. Entonces, en nuestra opinión la existencia de este límite no es tan obvia. Aquí es donde entrará en juego el NIP; lo usaremos para demostrar que este límite, de hecho, existe. Los detalles están en el siguiente problema.

Ejercicio$\PageIndex{5}$

El propósito de este problema es mostrar que$\lim_{n \to \infty }\left (\left (1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \right ) - \ln (n+1) \right )$ existe.

Vamos$x_n = \left (1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \right ) - \ln (n+1)$. Utilice el siguiente diagrama para mostrar$x_1 ≤ x_2 ≤ x_3 ≤···$

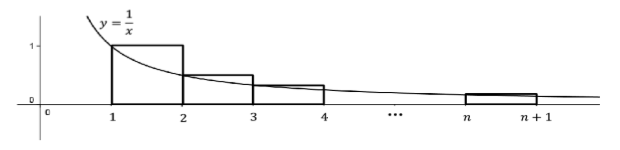
$higo 7.1.7.png$

Figura$\PageIndex{7}$: Diagrama para ejercicio$\PageIndex{5}$.

Vamos$z_n = \ln (n+1) - \left (\frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n+1} \right )$. Usa un diagrama similar para mostrarlo$z_1 ≤ z_2 ≤ z_3 ≤···$.
Vamos$y_n = 1 - z_n$. Mostrar que ($x_n$) y ($y_n$) satisfacen las hipótesis de la propiedad de intervalo anidado y utilizan el NIP para concluir que hay un número real$γ$ tal que$x_n ≤ γ ≤ y_n$ para todos$n$.
Concluir eso$\lim_{n \to \infty }\left (\left (1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \right ) - \ln (n+1) \right ) = \gamma$.

Ejercicio$\PageIndex{6}$

Usa el hecho de que$x_n ≤ γ ≤ y_n$ para todos aproximarse$n$$γ$ a tres decimales.

Ejercicio$\PageIndex{7}$

Utilice el hecho de que para grandes$n$,$1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \approx \ln (n+1) + \gamma$ para determinar aproximadamente qué tan grande$n$ debe ser para hacer\[1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \geq 100\]
Supongamos que tenemos una supercomputadora que puede agregar$10$ billones de términos de la Serie Armónica por segundo. Aproximadamente, ¿cuántas duraciones terrestres tardaría en que esta computadora resuma la Serie Armónica hasta superar los 100?

Search

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

teorema\(\PageIndex{1}\)

Ejercicio\(\PageIndex{3}\)

teorema\(\PageIndex{2}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)