7.4: El supremo y el teorema del valor extremo

Objetivos de aprendizaje

• Explicar supremo y el teorema del valor extremo

El teorema 7.3.1 dice que una función continua en un intervalo cerrado y delimitado debe ser acotada. La generosidad, en y por sí misma, no asegura la existencia de un máximo o mínimo. También debemos tener un intervalo cerrado, acotado. Para ilustrar esto, considere la función continua\(f(x) =tan^{-1}x\) definida en el intervalo (ilimitado)\((-∞,∞)\).

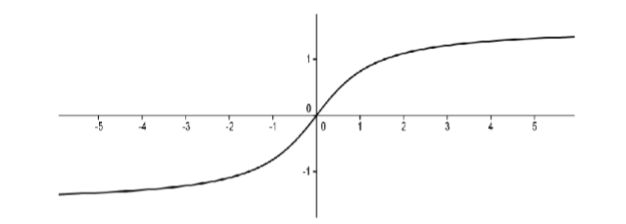
Figura\(\PageIndex{1}\): Gráfica de\(f(x) =tan^{-1}x\).

Esta función está delimitada entre\(-\frac{π}{2}\) y\(\frac{π}{2}\), pero no alcanza un máximo o mínimo ya que las líneas\(y = ±\frac{π}{2}\) son asíntotas horizontales. Observe que si restringimos el dominio a un intervalo cerrado y delimitado entonces alcanzaría sus valores extremos en ese intervalo (como lo garantiza la EVT).

Para encontrar un máximo necesitamos encontrar el límite superior más pequeño posible para el rango de la función. Esto solicita las siguientes definiciones.

Definición:\(\PageIndex{1}\)

Dejemos\(S ⊆ R\) y dejemos\(b\) ser un número real. Decimos que\(b\) es un límite superior de\(S\) previsto\(b ≥ x\) para todos\(x ∈ S\).

Por ejemplo, si\(S = (0,1)\), entonces cualquiera\(b\) con\(b ≥ 1\) sería un límite superior de\(S\). Además, el hecho de que no\(b\) sea un elemento del conjunto\(S\) es inmaterial. En efecto, si\(T = [0,1]\), entonces cualquiera\(b\) con\(b ≥ 1\) seguiría siendo un límite superior de\(T\). Observe que, en general, si un conjunto tiene un límite superior, entonces tiene infinitamente muchos ya que cualquier número mayor que ese límite superior también sería un límite superior. Sin embargo, hay algo especial en el límite superior más pequeño.

Definición:\(\PageIndex{2}\)

Dejemos\(S ⊆ R\) y dejemos\(b\) ser un número real. Decimos que\(b\) es el límite inferior superior de\(S\) proporcionado

1. \(b ≥ x\)para todos\(x ∈ S\). (\(b\)es un límite superior de\(S\))
2. Si\(c ≥ x\) por todos\(x ∈ S\), entonces\(c ≥ b\). (Cualquier límite superior de\(S\) es al menos tan grande como\(b\))

En este caso, también decimos que\(b\) es lo supremo de\(S\) y escribimos

\[b = \sup(S)\]

Observe que la definición realmente dice que\(b\) es el límite superior más pequeño de\(S\). También observe que la segunda condición puede ser reemplazada por su contrapositiva por lo que podemos decir que\(b = \sup S\) si y solo si

1. \(b ≥ x\)para todos\(x ∈ S\)
2. Si\(c < b\) entonces existe\(x ∈ S\) tal que\(c < x\)

La segunda condición dice que si un número\(c\) es menor que\(b\), entonces no puede ser un límite superior, entonces ese es\(b\) realmente el límite superior más pequeño.

Observe también que el supremo del conjunto puede o no estar en el propio conjunto. Esto se ilustra con los ejemplos anteriores como en ambos casos,\(1 = \sup (0,1)\) y\(1 = \sup [0,1]\). Obviamente, un conjunto que no está delimitado por encima como\(N = {1, 2, 3, ...}\) no puede tener un supremo. Sin embargo, para los conjuntos no vacíos que están delimitados arriba, tenemos lo siguiente.

Teorema\(\PageIndex{1}\): The Least Upper Bound Property (LUBP)

Let\(S\) Ser un subconjunto no vacío del\(R\) cual está delimitado arriba. Entonces\(S\) tiene un supremo.

Croquis de Prueba

Desde\(S \neq \varnothing\) entonces existe\(s ∈ S\). Ya que\(S\) está acotado por encima entonces tiene un límite superior, digamos\(b\). Nos prepararemos para usar la Propiedad Intervalo Anidado. Con esto en mente, dejar\(x_1 = s\)\(y_1 = b\) y notar que\(∃ x ∈ S\) tal que\(x ≥ x_1\) (es decir,\(x_1\) sí mismo) y\(∀ x ∈ S\),\(y_1 ≥ x\). Probablemente adivinaste lo que viene después: deja\(m_1\) ser el punto medio de\([x_1,y_1]\). Observe que cualquiera\(m_1 ≥ x\),\(∀x ∈ S\) o\(∃ x ∈ S\) tal que\(x ≥ m_1\). En el primer caso, remarcamos, dejando\(x_2 = x_1\) y\(y_2 = m_1\). En este último caso, dejamos\(x_2 = m_1\) y\(y_2 = y_1\). En cualquier caso, terminamos con\(x_1 ≤ x_2 ≤ y_2 ≤ y_1, y_2 - x_2 = \frac{1}{2} (y_1 - x_1)\), y\(∃ x ∈ S\) tal que\(x ≥ x_2\) y\(∀x ∈ S\),\(y_2 ≥ x\). Si continuamos con este proceso, terminamos con dos secuencias, (\(x_n\)) y (\(y_n\)), cumpliendo las siguientes condiciones:

1. \(x_1 ≤ x_2 ≤ x_3 ≤ ... \)
2. \(y_1 ≥ y_2 ≥ y_3 ≥ ...\)
3. \(∀ n, x_n ≤ y_n\)
4. \(\lim_{n \to \infty } (y_n - x_n) = \lim_{n \to \infty }\frac{1}{2^{n-1}} (y_1 - x_1) = 0\)
5. \(∀ n,∃ x ∈ S\)tal que\(x ≥ x_n\) y\(∀x ∈ S, y_n ≥ x\)

Por propiedades 1-5 y el NIP existe\(c\) tal que\(x_n ≤ c ≤ y_n, ∀ n\). Te dejaremos usar la propiedad 5 para demostrarlo\(c = \sup S\).

Ejercicio\(\PageIndex{1}\)

Completar las ideas anteriores para proporcionar una prueba formal del Teorema\(\PageIndex{1}\).

Observe que realmente usamos el hecho de que no\(S\) estaba vacío y delimitado arriba en la prueba del Teorema\(\PageIndex{1}\). Esto tiene sentido, ya que un conjunto que no está delimitado por encima no puede tener posiblemente un límite superior mínimo. De hecho, cualquier número real es un límite superior del conjunto vacío para que el conjunto vacío no tenga un límite superior mínimo.

El siguiente corolario al Teorema\(\PageIndex{1}\) puede ser muy útil.

Corolario\(\PageIndex{1}\)

Let (\(x_n\)) ser una secuencia acotada y creciente de números reales. Es decir,\(x_1 ≤ x_2 ≤ x_3 ≤···\). Entonces (\(x_n\)) converge a algún número real\(c\).

Ejercicio\(\PageIndex{2}\)

Demostrar Corolario\(\PageIndex{1}\).

Pista

Vamos\(c = \sup {x_n|n = 1,2,3,...}\). Para demostrar eso\(\lim_{n \to \infty } x_n = c\), vamos\(\epsilon > 0\). Tenga en cuenta que no\(c - \epsilon\) es un límite superior. ¡Lo tomas de aquí!

Ejercicio\(\PageIndex{3}\)

Considera la siguiente curiosa expresión\(\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{\cdots }}}}\). Usaremos Corolario\(\PageIndex{1}\) para demostrar que esto realmente converge a algún número real. Después de que sepamos que converge podemos realmente calcular lo que es. Por supuesto para hacerlo, necesitamos definir las cosas un poco más precisamente. Con esto en mente consideremos la siguiente secuencia (\(x_n\)) definida de la siguiente manera:

\[x_1 = \sqrt{2}\]

\[x_{n+1} = \sqrt{2+x_n}\]

1. Utilice la inducción para mostrar que\(x_n < 2\) para\(n = 1, 2, 3, ....\)
2. Utilice el resultado de la parte (a) para mostrarlo\(x_n < x_{n+1}\) para\(n = 1, 2, 3, ...\)
3. De Corolario\(\PageIndex{1}\), tenemos que (\(x_n\)) debe converger a algún número\(c\). Usa el hecho de que (\(x_{n+1}\)) debe converger a\(c\) también para computar lo que\(c\) debe ser.

Ahora tenemos todas las herramientas que necesitamos para abordar el Teorema del Valor Extremo.

Teorema\(\PageIndex{2}\): Extreme Value Theorem (EVT)

Supongamos que\(f\) es continuo en\([a,b]\). Entonces existe\(c\),\(d ∈ [a,b]\) tal que\(f(d) ≤ f(x) ≤ f(c)\), para todos\(x ∈ [a,b]\).

Croquis de techo P

Primero mostraremos que\(f\) alcanza su máximo. Para ello, recordemos que el Teorema del Teorema 7.3.1 nos dice que\(f[a,b] = {f(x)|x ∈ [a,b]}\) es un conjunto acotado. Por la LUBP,\(f[a,b]\) debe tener un límite inferior superior que etiquetaremos\(s\), así que eso\(s = \sup f[a,b]\). Esto dice eso\(s ≥ f(x)\), para todos\(x ∈ [a,b]\). Todo lo que tenemos que hacer ahora es encontrar un\(c ∈ [a,b]\) con\(f(c) = s\). Con esto en mente, observe que ya que\(s = \sup f[a,b]\), entonces para cualquier entero positivo\(n\), no\(s - \frac{1}{n}\) es un límite superior de\(f[a,b]\). Así existe\(x_n ∈ [a,b]\) con\(s - \frac{1}{n} < f(x_n) \leq s\). Ahora, por el Teorema de Bolzano-Weierstrass, (\(x_n\)) tiene una subsecuencia convergente (\(x_{n_k}\)) que converge a algunos\(c ∈ [a,b]\). Usando la continuidad de\(f\) at\(c\), deberías poder demostrarlo\(f(c) = s\). Para encontrar el mínimo de\(f\), encontrar el máximo de\(-f\).

Ejercicio\(\PageIndex{4}\)

Formalizar las ideas anteriores en una prueba de Teorema\(\PageIndex{2}\).

Observe que utilizamos el NIP para probar tanto el Teorema de Bolzano-Weierstrass como el LUBP. Esto es realmente inevitable, pues resulta que todas esas afirmaciones son equivalentes en el sentido de que cualquiera de ellas puede tomarse como el axioma de integridad para el sistema numérico real y las demás demostradas como teoremas. Esto no es raro en matemáticas, ya que las personas tienden a gravitar hacia ideas que se adaptan al problema particular en el que están trabajando. En este caso, la gente se dio cuenta en algún momento de que necesitaban algún tipo de propiedad de integridad para que el sistema de números reales demostrara varios teoremas. La formulación de integridad de cada individuo encaja con su comprensión del problema en cuestión. Sólo en retrospectiva vemos que realmente estaban hablando del mismo concepto: la integridad del sistema de números reales. De hecho, la mayoría de los libros de texto modernos utilizan la LUBP como axioma de la completitud y prueban todas las demás formulaciones como teoremas. Terminaremos esta sección mostrando que ya sea el Teorema de Bolzano-Weierstrass o el LUBP pueden ser utilizados para probar el NIP. Esto dice que todos son equivalentes y que cualquiera de ellos podría ser tomado como el axioma de integridad.

Ejercicio\(\PageIndex{5}\)

Utilizar el Teorema de Bolzano-Weierstrass para probar el NIP. Es decir, supongamos que el Teorema de Bolzano-Weierstrass sostiene y supongamos que tenemos dos secuencias de números reales, (\(x_n\)) y (\(y_n\)), satisfaciendo:

1. \(x_1 ≤ x_2 ≤ x_3 ≤ ... \)
2. \(y_1 ≥ y_2 ≥ y_3 ≥ ... \)
3. \(∀ n, x_n ≤ y_n \)
4. \(\lim_{n \to \infty } (y_n - x_n) = 0\)

Demostrar que hay un número real\(c\) tal que\(x_n ≤ c ≤ y_n\), para todos\(n\).

Dado que el Teorema de Bolzano-Weierstrass y la Propiedad de Intervalo Anidado son equivalentes, se deduce que el Teorema de Bolzano-Weierstrass no funcionará para el sistema numérico racional.

Ejercicio\(\PageIndex{6}\)

Encontrar una secuencia acotada de números racionales tal que ninguna subsecuencia de la misma converja a un número racional.

Ejercicio\(\PageIndex{7}\)

Utilice la Propiedad Límite Mínimo Superior para probar la Propiedad Intervalo Anidado. Es decir, supongamos que cada subconjunto no vacío de los números reales que está delimitado arriba tiene un límite mínimo superior; y supongamos que tenemos dos secuencias de números reales (\(x_n\)) y (\(y_n\)), satisfaciendo:

1. \(x_1 ≤ x_2 ≤ x_3 ≤ ... \)
2. \(y_1 ≥ y_2 ≥ y_3 ≥ ...\)
3. \(∀ n, x_n ≤ y_n\)
4. \(\lim_{n \to \infty } (y_n - x_n) = 0\)

Demostrar que existe un número real\(c\) tal que\(x_n ≤ c ≤ y_n\), para todos\(n\). (Nuevamente, la\(c\) voluntad, por necesidad, será única, pero no te preocupes por eso).

Pista

El corolario\(\PageIndex{1}\) podría funcionar bien aquí.

Ejercicio\(\PageIndex{8}\)

Dado que el LUBP es equivalente al NIP no se sostiene para el sistema numérico racional. Demuéstralo encontrando un conjunto no vacío de números racionales que está delimitado arriba, pero cuyo supremo es un número irracional.

Tenemos la maquinaria en su lugar para limpiar un asunto que se introdujo en el Capítulo 1. Si recuerda (o mira hacia atrás) presentamos la Propiedad Arquímedes del sistema de números reales. Esta propiedad dice que dados dos números reales positivos cualesquiera\(a,b\), existe un entero positivo\(n\) con\(na > b\). Como mencionamos en el Capítulo 1, esto se tomó como intuitivamente obvio. La analogía que utilizamos ahí fue a vaciar un océano\(b\) con una cucharilla\(a\) siempre que estemos dispuestos a usarlo suficientes veces\(n\). La integridad del sistema de números reales nos permite probarlo como teorema formal.

Teorema\(\PageIndex{3}\): Archimedean Property of \(\mathbb{R}\)

Dado cualquier número real positivo\(a\) y\(b\), existe un entero positivo\(n\), tal que\(na > b\).

Ejercicio\(\PageIndex{9}\)

Demostrar teorema\(\PageIndex{3}\).

Pista

Supongamos que hay números reales positivos\(a\) y\(b\), tal que\(na ≤ b, ∀ n ∈ N\). Entonces\(N\) estaría delimitado arriba por\(b/a\). Dejemos\(s = \sup (N)\) y consideremos\(s - 1\).

Dado lo que hemos estado haciendo, uno podría preguntarse si la Propiedad Arquímedea es equivalente a la LUBP (y así podría tomarse como axioma). La respuesta está en el siguiente problema.

Ejercicio\(\PageIndex{10}\)

¿\(\mathbb{Q}\)Satisface la Propiedad Arquímedes y qué tiene esto que ver con la cuestión de tomar la Propiedad de Arquímedes como axioma de integridad?