1.11: El registro de funciones (z)
- Page ID
- 109924
Nuestro objetivo en esta sección es definir la función log. Queremos\(\text{log} (z)\) ser la inversa de\(e^z\). Es decir, queremos\(e^{\text{log} (z)} = z\). Veremos que\(\text{log} (z)\) es de múltiples valores, así que cuando lo usemos tendremos que especificar una sucursal.
Comenzamos por mirar el ejemplo más simple que ilustra que\(\text{log} (z)\) es de múltiples valores.
Encuentra\(\text{log} (1)\).
Solución
Eso lo sabemos\(e^{0} = 1\), así\(\text{log} (1) = 0\) es una respuesta.
Eso también lo sabemos\(e^{2\pi i} = 1\), así\(\text{log} (1) = 2\pi i\) es otra posible respuesta. De hecho, podemos elegir cualquier múltiplo de\(2\pi i\):
\[\text{log} (1) = 2n \pi i \nonumber\]
donde\(n\) es cualquier entero.
Este ejemplo nos lleva a considerar la forma polar para\(z\) como tratamos de definir\(\text{log} (z)\). Si\(z = re^{i \theta}\) entonces un valor posible para\(\text{log} (z)\) es
\[ \begin{align*} \text{log} (z) &= \text{log} (re^{i \theta}) \\[4pt] &= \text{log} (r) + i \theta, \end{align*}\]
aquí\(\text{log} (r)\) está el logaritmo habitual de un número positivo real. Para la completitud mostramos explícitamente que con esta definición\(e^{\text{log} (z)} = z\):
\[\begin{align*} e^{\text{log} (z)} &= e^{\text{log} (r) + i \theta} \\[4pt] &= e^{\text{log} (r)} e^{i \theta} \\[4pt] &= re^{i \theta} \\[4pt] &= z \end{align*}\]
Desde\(r = |z|\) y\(\theta = \text{arg} (z)\) hemos llegado a nuestra definición.
La función\(\text{log} (z)\) se define como
\[\text{log} (z) = \text{log} (|z|) + i \text{arg} (z),\]
donde\(\text{log} (|z|)\) está el logaritmo natural habitual de un número real positivo.
Observaciones.
- Ya que\(\text{arg} (z)\) tiene infinitamente muchos valores posibles, también lo hace\(\text{log} (z)\).
- \(\text{log} (0)\)no está definido. (Ambos porque no\(\text{arg} (0)\) está definido y no\(\text{log} (|0|)\) está definido.)
- Elegir una sucursal para\(\text{arg} (z)\) marcas\(\text{log} (z)\) únicas valoradas. La terminología habitual es decir que hemos elegido una rama de la función log.
- La rama principal del tronco proviene de la rama principal de arg. Es decir,
\(\text{log} (z) = \text{log} (|z|) + i \text{arg} (z)\), donde\(-\pi < \text{arg} (z) \le \pi\) (rama principal).
Calcular todos los valores de\(\text{log} (i)\). Especificar cuál proviene de la rama principal.
Solución
Tenemos eso\(|i| = 1\) y\(\text{arg} (i) = \dfrac{\pi}{2} + 2n \pi\), entonces
\[ \begin{align*} \text{log} (i) &= \text{log} (1) + i \dfrac{\pi}{2} + i 2n \pi \\[4pt] &= i \dfrac{\pi}{2} + i2n\pi, \end{align*}\]
donde\(n\) es cualquier entero.
La rama principal de\(\text{arg} (z)\) es entre\(-\pi\) y\(\pi\), entonces\(\text{Arg} (i) = \pi /2\). Por lo tanto, el valor de\(\text{log} (i)\) desde la rama principal es\(i \pi /2\).
Calcular todos los valores de\(\text{log} (-1 - \sqrt{3} i)\). Especificar cuál proviene de la rama principal.
Solución
Vamos\(z = -1 - \sqrt{3} i\). Entonces\(|z| = 2\) y en la rama principal\(\text{Arg} (z) = -2\pi /3\). Así que todos los valores de\(\text{log} (z)\) son
\[\text{log} (z) = \text{log} (2) - i \dfrac{2\pi}{3} + i2n \pi.\]
El valor de la rama principal es\(\text{log} (z) = \text{log} (2) - i 2\pi /3\).
Figuras que\(w = \text{log} (z)\) se muestran como un mapeo
Las siguientes figuras muestran diferentes aspectos del mapeo dado por\(\text{log}(z)\).
En la primera figura vemos que un punto\(z\) se mapea a (infinitamente) muchos valores de\(w\). En este caso mostramos\(\text{log} (1)\) (puntos azules),\(\text{log} (4)\) (puntos rojos),\(\text{log} (i)\) (cruz azul) y\(\text{log} (4i)\) (cruz roja). Los valores en la rama principal se encuentran dentro de la región sombreada en el\(w\) plano. Tenga en cuenta que los valores de\(\text{log}(z)\) para un dado se\(z\) colocan a intervalos de\(2\pi i\) en el\(w\) plano.
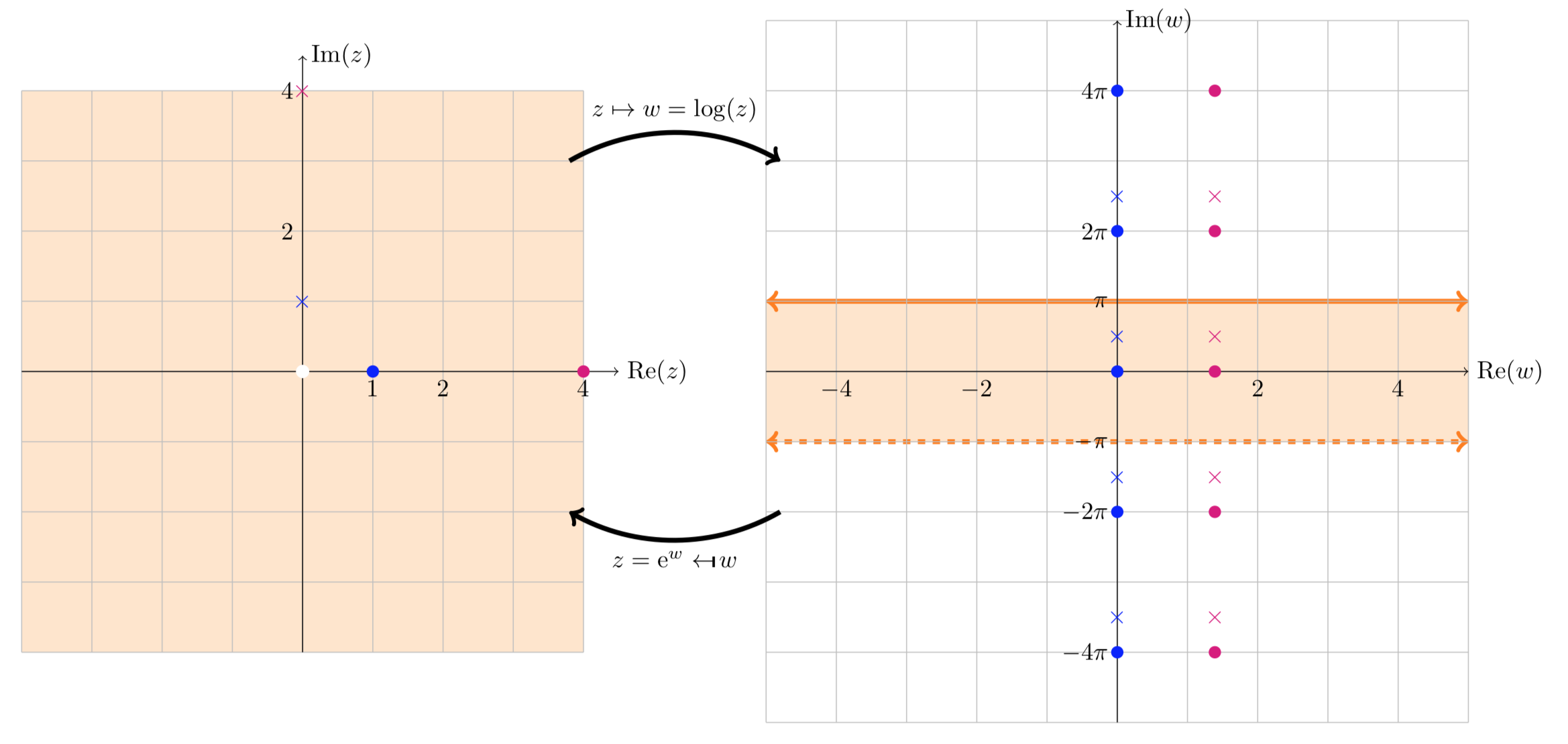
Mapeo\(\text{log} (z): \text{log} (1), \text{log} (4), \text{log} (i), \text{log} (4i)\)
La siguiente figura ilustra que la rama principal del registro mapea el plano perforado a la franja horizontal\(-\pi < \text{Im} (w) \le \pi\). Nuevamente mostramos los valores de\(\text{log} (1), \text{log} (4), \text{log} (i), \text{log} (4i)\). Como hemos elegido una sucursal, solo se muestra un valor para cada registro.
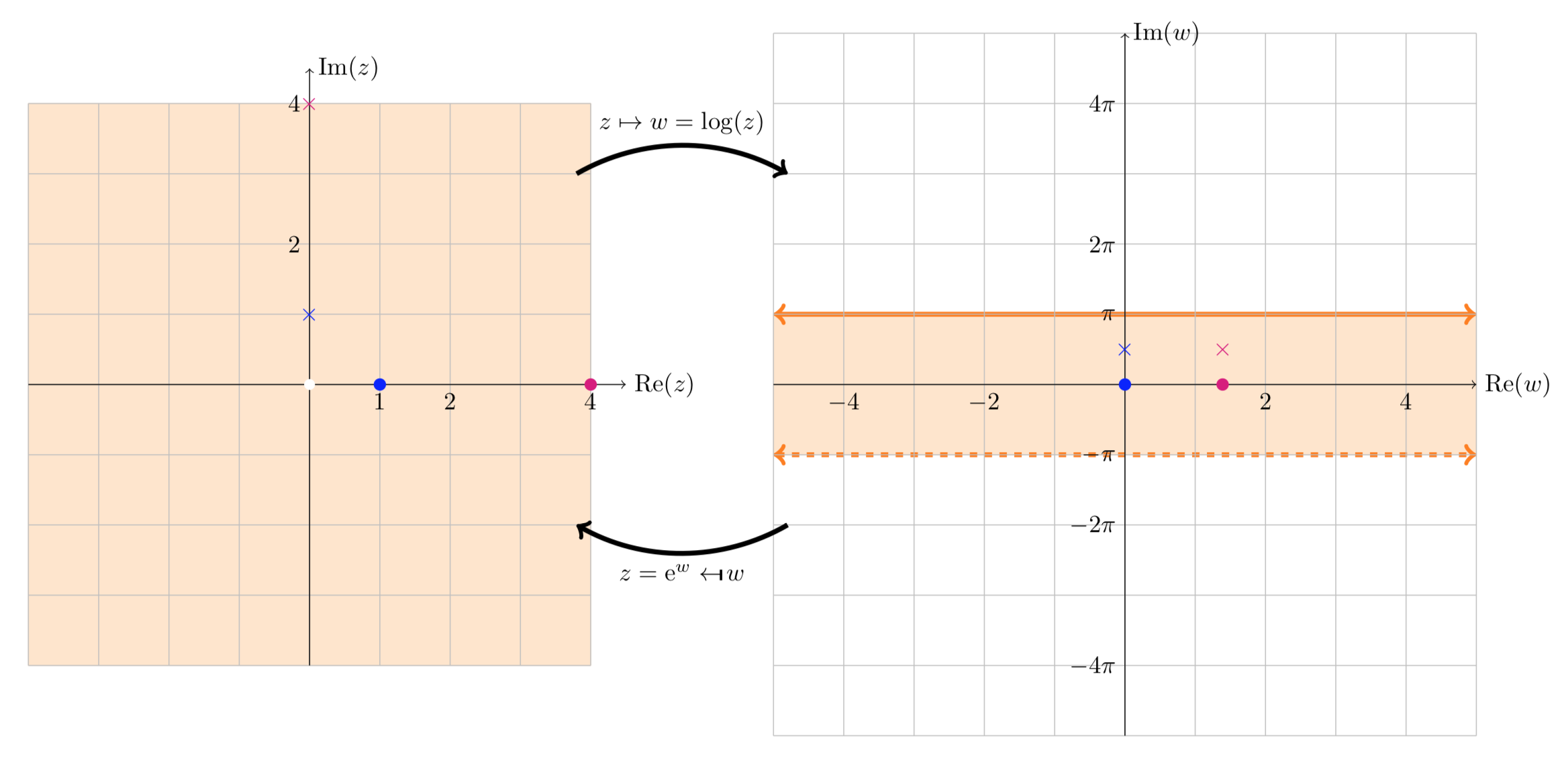
Mapeo\(\text{log} (z)\): la rama principal y el plano perforado
La tercera figura muestra cómo los círculos centrados en 0 se mapean a líneas verticales, y los rayos del origen se mapean a líneas horizontales. Si nos limitamos a la rama principal, los círculos se mapean a segmentos de línea verticales y los rayos a una sola línea horizontal en la región principal (sombreada) del\(w\) plano.
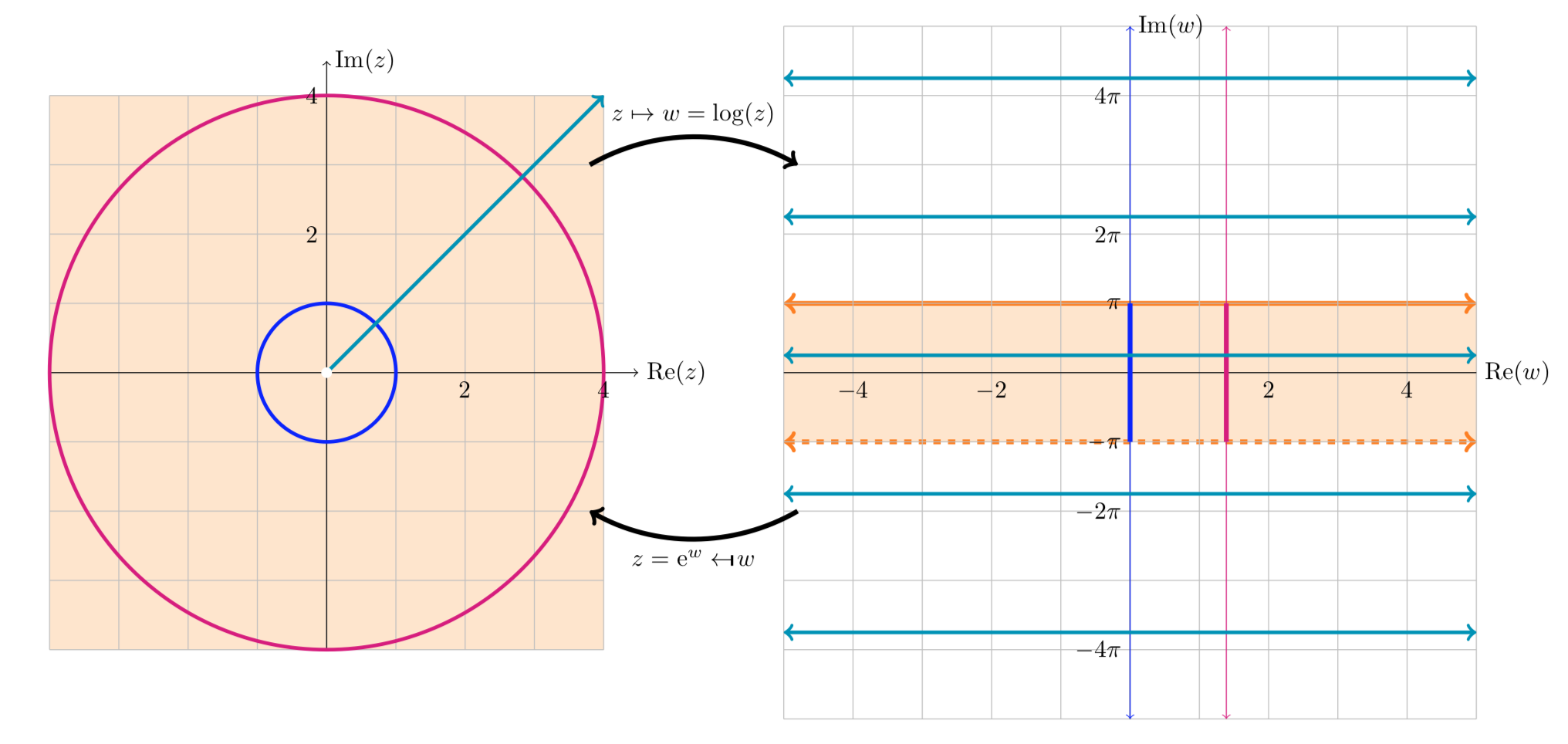
Mapeo\(\text{log} (z)\): mapeo de círculos y rayos
Poderes Complejos
Podemos usar la función log para definir potencias complejas.
Let\(z\) y\(a\) ser números complejos entonces el poder\(z^{a}\) se define como
\[z^a = e^{a \text{log} (z)}.\]
Esto es generalmente de múltiples valores, por lo que para especificar un solo valor se requiere elegir una rama de\(\text{log} (z)\).
Calcular todos los valores de\(\sqrt{2i}\). Dar el valor asociado a la rama principal de\(\text{log} (z)\).
Solución
Tenemos
\[\text{log} (2i) = \text{log} (2e^{\dfrac{i \pi}{2}}) = \text{log} (2) + i \dfrac{\pi} {2} + i2n \pi. \nonumber\]
Entonces,
\[\begin{align*} \sqrt{2i} &= (2i)^{1/2} \\[4pt] &= e^{\frac{\text{log} (2i)}{2}} \\[4pt] &= e^{\frac{\text{log} (2)}{2} + \dfrac{i\pi}{4} + in \pi} \\[4pt] &= \sqrt{2} e^{\dfrac{i\pi}{4} + in\pi}. \end{align*}\]
(Como de costumbre\(n\) es un número entero.) Como vimos antes, esto sólo da dos valores distintos. La rama principal tiene\(\text{Arg} (2i) = \pi /2\), por lo
\[\begin{align*} \sqrt{2i} &= \sqrt{2} e^{(\frac{i \pi }{4})} \\[4pt] &= \sqrt{2} \frac{(1 + i)}{\sqrt{2}} \\[4pt] &= 1 + i. \end{align*}\]
El otro valor distinto es cuando\(n = 1\) y da menos el valor justo por encima.
Raíces cubitas: Calcular todas las raíces cubicas de\(i\). Dar el valor que proviene de la rama principal de\(\text{log} (z)\).
Solución
Tenemos\(\text{log} (i) = i \dfrac{\pi}{2} + i 2n \pi\), donde\(n\) está cualquier entero. Entonces,
\(i^{1/3} = e^{\frac{\text{log} (i)}{3}} = e^{i \frac{\pi}{6} + i \frac{2n \pi}{3}}\)
Esto da solo tres valores distintos
\(e^{i\pi /6}, e^{i5\pi /6}, e^{i9\pi /6}\)
En la rama principal\(\text{log} (i) = i \dfrac{\pi}{2}\), por lo que el valor de\(i^{1/3}\) que proviene de esto es
\(e^{i\pi /6} = \dfrac{\sqrt{3}}{2} + \dfrac{i}{2}\).
Calcular todos los valores de\(1^{i}\). ¿Cuál es el valor de la rama principal?
Solución
Esto es similar a los problemas anteriores. \(\text{log} (1) = 2n\pi i\), entonces
\[1^{i} = e^{i \text{log} (1)} = e^{i2n\pi i} = e^{-2n\pi}, \nonumber\]
donde\(n\) es un entero.
\(\text{log} (1) = 0\)Así lo tiene el ramo principal\(1^i = 1\).


