4.4: Independencia del Camino

Última actualización
Guardar como PDF

Page ID: 109787

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Decimos que la integral$\int_{\gamma} f(z)\ dz$ es path in dependent si tiene el mismo valor para dos caminos cualesquiera con los mismos puntos finales. Más precisamente, si$f(z)$ se define en una región$A$ entonces$\int_{\gamma} f(z)\ dz$ es independiente de ruta en$A$, si tiene el mismo valor para dos rutas cualquiera$A$ con los mismos puntos finales.

El siguiente teorema se desprende directamente del teorema fundamental. La prueba utiliza el mismo argumento que el Ejemplo 4.3.2.

Teorema$\PageIndex{1}$

Si$f(z)$ tiene una antiderivada en una región abierta$A$, entonces la integral de ruta$\displaystyle \int_{\gamma} f(z)\ dz$ es independiente de camino para todos los caminos en$A$.

Prueba

Ya que$f(z)$ tiene una antiderivada de$f(z)$, el teorema fundamental nos dice que la integral solo depende de los puntos finales de$\gamma$, i.e.

\[\int_{\gamma} f(z) \ dz = F(z_1) - F(z_0) \nonumber\]

donde$z_0$ y$z_1$ son el punto inicial y final de$\gamma$.

Una forma alternativa de expresar la independencia del camino utiliza caminos cerrados.

Teorema$\PageIndex{2}$

Las dos cosas siguientes son equivalentes.

La integral$\displaystyle \int_{\gamma} f(z)\ dz$ es camino independiente.
La integral$\displaystyle \int_{\gamma} f(z)\ dz$ alrededor de cualquier camino cerrado es 0.

Prueba

Esto es esencialmente idéntico a la prueba multivariable equivalente. Tenemos que mostrar dos cosas:

La independencia del camino implica que la línea integral alrededor de cualquier camino cerrado es 0.
Si la línea integral alrededor de todos los caminos cerrados es 0 entonces tenemos independencia de camino.

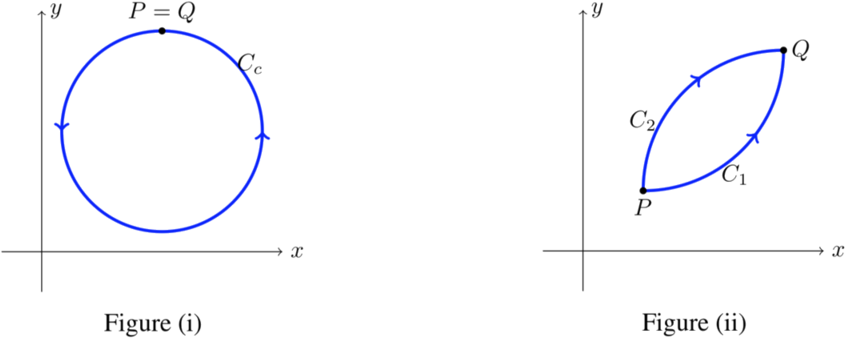
Para ver ($i$), asumir la independencia del camino y considerar los$C$ espectáculos de ruta cerrada en la figura (i) a continuación. Desde el punto de partida$z_0$ en el mismo que el punto final$z_1$ la integral$\int_C f(z)\ dz$ debe tener el mismo valor que la integral de línea sobre la curva que consiste en el punto único$z_0$. Ya que eso es claramente 0 debemos tener la integral sobre$C$ es 0.

Para ver ($ii$), asuma$\int_C f(z)\ dz = 0$ para cualquier curva cerrada. Considerar las dos curvas$C_1$ y$C_2$ se muestran en la figura (ii). Ambos comienzan en$z_0$ y terminan en$z_1$. Por el supuesto de que las integrales sobre caminos cerrados son 0 tenemos$\int_{C_1 - C_2} f(z)\ dz = 0$. Entonces,

\[f_{C_1} f(z)\ dz = \int_{C_2} f(z)\ dz. \nonumber\]

Es decir, dos caminos cualesquiera de$z_0$ para$z_1$ tener la misma línea integral. Esto demuestra que las integrales de línea son independientes de la ruta.

$imageedit_4_7910359843.png$