4.6: Teorema de Cauchy

Última actualización
Guardar como PDF

Page ID: 109808

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El teorema de Cauchy es análogo al teorema de Green para campos de vectores libres de rizo.

Teorema$\PageIndex{1}$ Cauchy's theorem

Supongamos que$A$ es una región simplemente conectada,$f(z)$ es analítica$A$ y$C$ es una simple curva cerrada en$A$. Entonces se mantienen las siguientes tres cosas:

(i)$\int_{C} f(z)\ dz = 0$

(i') Podemos dejar caer el requisito que$C$ es simple en la parte (i).

(ii) Las integrales de$f$ los caminos dentro$A$ son independientes del camino. Es decir, dos caminos con los mismos puntos finales se integran al mismo valor.

(iii)$f$ tiene un antiderivado en$A$.

Prueba

Demostraremos (i) usando el teorema de Green —podríamos dar una prueba que no dependiera de Green's, pero sería bastante similar en sabor a la prueba del teorema de Green.

Dejar$R$ ser la región dentro de la curva. Y escribir$f = u + iv$. Ahora escribimos la integral de la siguiente manera

\[\int_{C} f(z)\ dz = \int_{C} (u + iv) (dx + idy) = \int_{C} (u\ dx - v\ dy) + i(v \ dx + u\ dy).\]

Apliquemos el teorema de Green a las piezas reales e imaginarias por separado. Primero la pieza real:

\[\int_{C} u \ dx - v\ dy = \int_{R} (-v_x - u_y) \ dx\ dy = 0.\]

Así mismo para la pieza imaginaria:

\[\int_{C} v\ dx + u\ dy = \int_R (u_x - v_y) \ dx\ dy = 0.\]

Obtenemos 0 porque las ecuaciones de Cauchy-Riemann dicen$u_x = v_y$, así$u_x - v_y = 0$.

Para ver la parte (i′) debes dibujar algunas curvas que se crucen y convencerte de que se pueden romper en una suma de simples curvas cerradas. Así, (i′) se desprende de (i). (Para probar verdaderamente la parte (i′) necesitaríamos una definición más técnicamente precisa de simplemente conectado para poder decir que todas las curvas cerradas dentro$A$ pueden deformarse continuamente entre sí.)

La parte (ii) se desprende del (i) y el Teorema 4.4.2.

Para ver (iii), elija un punto base$z_0 \in A$ y deje

\[F(z) = \int_{z_0}^{z} f(w)\ dw.\]

Aquí el itnegral está por encima de cualquier camino en la$A$ conexión$z_0$ con$z$. Por parte (ii),$F(z)$ está bien definido. Si podemos demostrarlo$F'(z) = f(z)$ entonces ya terminaremos. Hacer esto equivale a manejar la notación para aplicar el teorema fundamental del cálculo y las ecuaciones de Cauchy-Riemann. Entonces, escribamos

\[f(z) = u(x, y) + iv (x, y),\ \ \ \ \ \ F(z) = U(x, y) + iV (x, y).\]

Entonces podemos escribir

\[\dfrac{\partial f}{\partial x} = u_x + iv_x, \text{etc.}\]

Podemos formular las ecuaciones de Cauchy-Riemann para$F(z)$

\[F'(z) = \dfrac{\partial F}{\partial x} = \dfrac{1}{i} \dfrac{\partial F}{\partial y}\]

i.e.

\[F'(z) = U_x + iV_x = \dfrac{1}{i} (U_y + i V_y) = V_y - i U_y.\]

Como referencia, observamos que usando la ruta$\gamma (t) = x(t) + iy (t)$, con$\gamma (0) = z_0$ y$\gamma (b) = z$ tenemos

\[\begin{array} {rcl} {F(z) = \int_{z_0}^{z} f(w)\ dw} & = & {\int_{z_0}^{z} (u (x, y) + iv(x, y)) (dx + idy)} \\ {} & = & {\int_0^b (u(x(t), y(t)) + iv (x(t), y(t)) (x'(t) + iy'(t))\ dt.} \end{array}\]

Nuestro objetivo ahora es demostrar que las ecuaciones de Cauchy-Riemann dadas en la Ecuación 4.6.9 se mantienen para$F(z)$. La siguiente figura muestra una ruta arbitraria de$z_0$ a$z$, que se puede utilizar para calcular$f(z)$. Para calcular los parciales de$F$ vamos a necesitar las líneas rectas que$C$ continúan$z + h$ o$z + ih$.

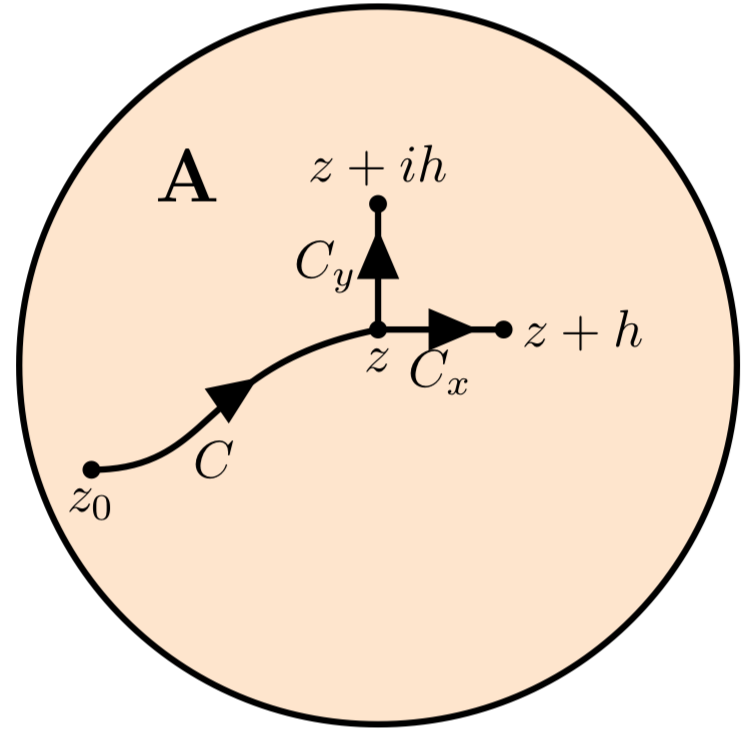
$2020-09-06 5.39.03.png$
Caminos para probar el teorema de Cauchy

Para preparar el resto del argumento le recordamos que el teorema fundamental del cálculo implica

\[\lim_{h \to 0} \dfrac{\int_0^h g(t)\ dt}{h} = g(0).\]

(Es decir, la derivada de la integral es la función original.)

Primero vamos a ver$\dfrac{\partial F}{\partial x}$. Entonces, arregla$z = x + iy$. Mirando los caminos en la figura anterior tenemos

\[F(z + h) - F(z) = \int_{C + C_x} f(w)\ dw - \int_C f(w) \ dw = \int_{C_x} f(w)\ dw.\]

La curva$C_x$ es parametrizada por$\gamma (t) + x + t + iy$, con$0 \le t \le h$. Entonces,

\[\begin{array} {rcl} {\dfrac{\partial F} {\partial x} = \lim_{h \to 0} \dfrac{F(z + h) - F(z)}{h}} & = & {\lim_{h \to 0} \dfrac{\int_{C_x} f(w)\ dw}{h}} \\ {} & = & {\lim_{h \to 0} \dfrac{\int_{0}^{h} u(x + t, y) + iv(x + t, y)\ dt}{h}} \\ {} & = & {u(x, y) + iv(x, y)} \\ {} & = & {f(z).} \end{array}\]

La segunda a la última igualdad se desprende de la Ecuación 4.6.10.

Del mismo modo, obtenemos (recuerda:$w = z + it$, entonces$dw = i\ dt$)

\[\begin{array} {rcl} {\dfrac{1}{i} \dfrac{\partial F}{\partial y} = \lim_{h \to 0} \dfrac{F(z + ih) - F(z)}{ih}} & = & {\lim_{h \to 0} \dfrac{\int_{C_y} f(w) \ dw}{ih}} \\ {} & = & {\lim_{h \to 0} \dfrac{\int_{0}^{h} u(x, y + t) + iv (x, y + t) i \ dt}{ih}} \\ {} & = & {u(x, y) + iv(x, y)} \\ {} & = & {f(z).} \end{array}\]

Juntos las Ecuaciones 4.6.12 y 4.6.13 muestran

\[f(z) = \dfrac{\partial F}{\partial x} = \dfrac{1}{i} \dfrac{\partial F}{\partial y}\]

Por la Ecuación 4.6.7 hemos demostrado que$F$ es analítico y$F' = f$.