13.8: Laplace inversa
- Page ID
- 109763
Hasta ahora hemos calculado la transformada inversa de Laplace por búsqueda de tablas. Por ejemplo,\(\mathcal{L}^{-1} (1/(s - a)) = e^{at}\). Para hacer esto correctamente debemos primero verificar que la transformada de Laplace tenga una inversa.
Empezamos con las malas noticias: Desafortunadamente esto no es estrictamente cierto. Hay muchas funciones con la misma transformación de Laplace. Enumeramos algunas de las formas en que esto puede suceder.
- Si es\(f(t) = g(t)\) por\(t \ge 0\), entonces claramente\(F(s) = G(s)\). Dado que la transformación de Laplace solo se refiere\(t \ge 0\), las funciones pueden diferir completamente para\(t < 0\).
- Supongamos\(f(t) = e^{at}\) y
\[g(t) = \begin{cases} f(t) & \text{ for } t \ne 1 \\ 0 & \text{ for } t = 1. \end{cases}\]
Es decir,\(f\) y\(g\) son los mismos salvo que arbitrariamente les asignamos diferentes valores en\(t = 1\). Entonces, dado que las integrales no notarán la diferencia en un momento dado,\(F(s) = G(s) = 1/(s - a)\). En este sentido es imposible definir de\(\mathcal{L}^{-1} (F)\) manera única.
La buena noticia es que la inversa existe siempre y cuando consideremos dos funciones que sólo difieren en un conjunto insignificante de puntos iguales. En particular, podemos hacer la siguiente afirmación.
Supongamos\(f\) y\(g\) son continuos y\(F(s) = G(s)\) para todos\(s\) con\(\text{Re} (s) > a\) para algunos\(a\). Entonces\(f(t) = g(t)\) para\(t \ge 0\).
Este teorema se puede afirmar de una manera que incluye funciones continuas por partes. Tal afirmación tiene más cuidado, lo que oscurecería el punto básico de que la transformación de Laplace tiene una inversa única hasta algunas, para nosotros, diferencias triviales.
Comenzamos con algunos ejemplos que podemos calcular directamente.
Vamos
\[f(t) = e^{at}.\]
Entonces,
\[F(s) = \dfrac{1}{s - a}.\]
Mostrar
\[f(t) = \sum \text{Res} (F(s) e^{st})\]
\[f(t) = \dfrac{1}{2\pi i} \int_{c - i\infty}^{c + i \infty} F(s) e^{st}\ ds\]
La suma está sobre todos los polos de\(e^{st}/(s - a)\). Como es habitual, sólo consideramos\(t > 0\).
Aquí,\(c > \text{Re} (a)\) y la integral significa el camino integral a lo largo de la línea vertical\(x = c\).
Solución
Demostrar la Ecuación 13.8.4 es sencillo: Está claro que
\[\dfrac{e^{st}}{s -a}\]
tiene solo un polo que está en\(s = a\). Dado que,
\[\sum \text{Res} (\dfrac{e^{st}}{s - a}, a) = e^{at}\]
hemos probado la Ecuación 13.8.4.
Demostrar la Ecuación 13.8.5 está más involucrada. Primero debemos verificar la convergencia de la integral. En este caso,\(s = c + iy\), por lo que la integral es
\[\dfrac{1}{2\pi i} \int_{c - i \infty}^{c + i \infty} F(s) e^{st} \ ds = \dfrac{1}{2\pi i} \int_{-\infty}^{\infty} \dfrac{e^{(c + iy)t}}{c + iy - a} i \ dy = \dfrac{e^{ct}}{2 \pi} \int_{-\infty}^{\infty} \dfrac{e^{iyt}}{c + iy - a} \ dy.\]
La convergencia (condicional) de esta integral sigue usando exactamente el mismo argumento que en el ejemplo cerca del final del Tema 9 sobre la fórmula de inversión de Fourier para\(f(t) = e^{at}\). Es decir, el integrando es una oscilación en descomposición, alrededor de 0, por lo que su integral es también una oscilación en descomposición alrededor de algún valor limitante.
Ahora usamos el contorno que se muestra a continuación.
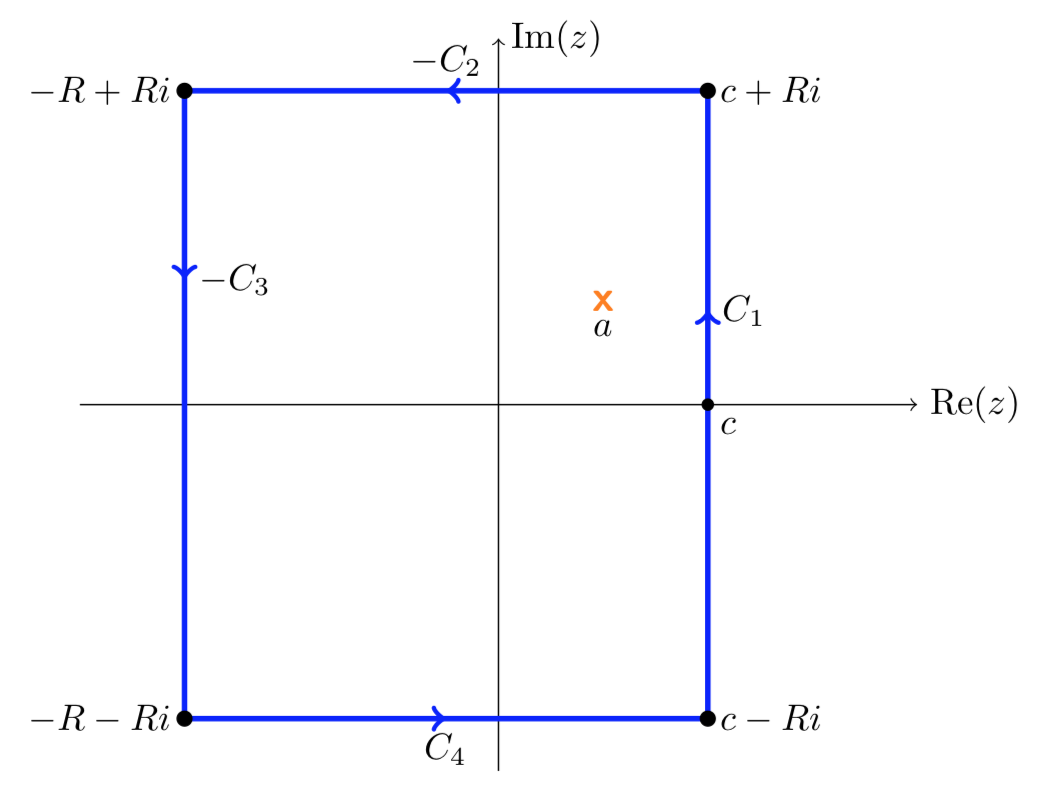
Dejaremos\(R\) ir al infinito y utilizaremos los siguientes pasos para probar la Ecuación 13.8.5.
- El teorema del residuo garantiza que si la curva es lo suficientemente grande como para contener\(a\) entonces
\[\dfrac{1}{2\pi i} \int_{C_1 - C_2 - C_3 + C_4} \dfrac{e^{st}}{s - a}\ ds = \sum \text{Res} (\dfrac{e^{st}}{s - a}, a) = e^{at}.\] - En un momento mostraremos que las integrales sobre\(C_2, C_3, C_4\) todo van a 0 as\(R \to \infty\).
- Claramente como\(R\) va al infinito, la integral sobre\(C_1\) va a la integral en la Ecuación 13.8.5 Armando estos pasos tenemos
\[e^{at} = \lim_{R \to \infty} \int_{C_1 - C_2 - C_3 + C_4} \dfrac{e^{st}}{s - a} \ ds = \int_{c - i\infty}^{c + i\infty} \dfrac{e^{st}}{s - a} \ ds\]
A excepción de probar las afirmaciones en el paso 2, esto prueba la Ecuación 13.8.5.
Para verificar el paso 2 miramos un lado a la vez.
\(C_2\):\(C_2\) está parametrizado por\(s = \gamma (u) = u + iR\), con\(-R \le u \le c\). Entonces,
\[|\int_{C_2} \dfrac{e^{st}}{s - a} \ ds| = \int_{-R}^{c} |\dfrac{e^{(u + iR)t}}{u + iR - a}| \le \int_{-R}^{c} \dfrac{e^{ut}}{R} \ du = \dfrac{e^{ct} - e^{-Rt}}{tR}.\]
Ya que\(c\) y\(t\) son fijos, está claro que esto va a 0 como\(R\) va al infinito.
La parte inferior\(C_4\) se maneja exactamente de la misma manera que la parte superior\(C_2\).
\(C_3\):\(C_3\) está parametrizado por\(s = \gamma (u) = -R + iu\), con\(-R \le u \le R\). Entonces,
\[|\int_{C_3} \dfrac{e^{st}}{s - a} \ ds| = \int_{-R}^{R} |\dfrac{e^{(-R + iu)t}}{-R + iu - a}| \le \int_{-R}^{R} \dfrac{e^{-Rt}}{R + a} \ du = \dfrac{e^{-Rt}}{R + a} \int_{-R}^{R} \ du = \dfrac{2\text{Re}^{-Rt}}{R+a}.\]
Ya que\(a\) y\(t > 0\) son fijos, está claro que esto va a 0 como\(R\) va al infinito.
Repita el ejemplo anterior con\(f(t) = t\) for\(t > 0\),\(F(s) = 1/s^2\).
Esto es similar al ejemplo anterior. Dado que\(F\) decae como en realidad\(1/s^2\) podemos permitir\(t \ge 0\)
Supongamos que\(f\) es continuo y de tipo exponencial\(a\). Entonces para\(c > a\) nosotros tenemos
\[f(t) = \dfrac{1}{2\pi i} \int_{c - i\infty}^{c + i\infty} F(s) e^{st}\ ds.\]
Como de costumbre, esta fórmula se mantiene para\(t > 0\).
- Prueba
-
La prueba utiliza la fórmula de inversión de Fourier. Simplemente aceptaremos este teorema por ahora. El ejemplo 13.8.1 anterior ilustra el teorema.
Supongamos que\(F(s)\) tiene un número finito de polos y decae como\(1/s\) (o más rápido). Definir
\[f(t) = \sum \text{Res} (F(s) e^{st}, p_k), \text{ where the sum is over all the poles } p_k.\]
Entonces\(\mathcal{L} (f; s) = F(s)\)
- Prueba
-
Prueba entregada en clase. Para ser agregado aquí. Las ideas básicas están presentes en los ejemplos anteriores, aunque requiere una elección bastante inteligente de contornos.
La fórmula de inversión integral en la Ecuación 13.8.13 puede verse\(f(t)\) como escritura como una 'suma' de exponenciales. Esto es sumamente útil. Por ejemplo, para un sistema lineal si sabemos cómo responde el sistema a la entrada\(f(t) = e^{at}\) para todos\(a\), entonces sabemos cómo responde a cualquier entrada escribiéndola como una 'suma' de exponenciales.


