14.1: Continuación analítica

Si tenemos una función analítica en una región\(A\), a veces podemos extender la función para que sea analítica en una región más grande. Esto se llama continuación analítica.

Ejemplo\(\PageIndex{1}\)

Considere la función

\[F(z) = \int_{0}^{\infty} e^{3t} e^{-zt} \ dt. \nonumber\]

Reconocemos esto como la transformación de Laplace de\(f(t) = e^{3t}\) (aunque cambiamos la variable de\(s\) a\(z\)). La integral converge absolutamente y\(F\) es analítica en la región\(A = \{\text{Re} (z) > 3\}\).

¿Podemos extender\(F(z)\) para ser analíticos en una región más grande\(B\)? Es decir, ¿podemos encontrar una región\(B\) una función\(\hat{F} (z)\) tal que

1. \(B\)contiene\(A\)
2. \(\hat{F} (z)\)es analítico en\(B\)
3. \(\hat{F} (z)\)está de acuerdo con\(F\) on\(A\), es decir,\(\hat{F} (z) = F(z)\) para\(z \in A\).

Solución

¡Sí! Sabemos que\(F(z) = \dfrac{1}{z - 3}\) -válido para cualquier\(z\) en\(A\). Entonces podemos definir\(\hat{F} (z) = \dfrac{1}{z - 3}\) para cualquiera\(z\) en\(B = C - \{3\}\).

Decimos que desde el punto de vista analítico hemos seguido\(F\)\(\hat{F}\) adelante\(A\)\(B\).

Nota

Normalmente no renombramos la función. Simplemente diríamos que\(F(z)\) definido por la Ecuación 14.2.1 puede continuar\(F(z) = \dfrac{1}{z - 3}\) encendido\(B\).

Definición: Continuación analítica

Supongamos que\(f(z)\) es analítico en una región\(A\). Supongamos también que\(A\) está contenido en una región\(B\). Decimos que se\(f\) puede continuar analíticamente de\(A\) a\(B\) si hay una función\(\hat{f} (z)\) tal que

1. \(\hat{f} (z)\)es analítico en\(B\).
2. \(\hat{f} (z) = f(z)\)para todos\(z\) en\(A\).

Como se señaló anteriormente, generalmente solo usamos el mismo símbolo\(f\) para la función on\(A\) y su continuación a\(B\).

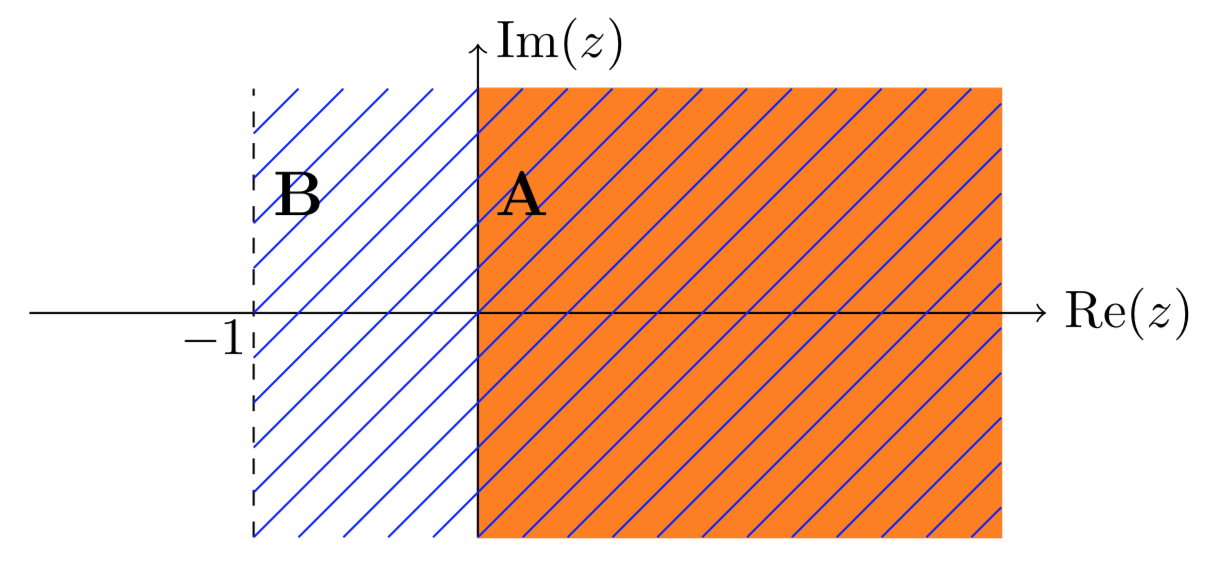
La región\(A = \text{Re} (z) > 0\) está contenida en\(B = \text{Re} (z) > -1\).

Nota

Utilizamos la continuación analítica implícitamente en, por ejemplo, la fórmula de inversión de Laplace que involucra residuos de\(F(s) = \mathcal{L} (f;s)\). Recordemos que escribimos eso para\(f(t) = e^{3t}\),\(F(s) = \dfrac{1}{s - 3}\) y

\[f(t) = \sum \text{ residues of } F.\]

Como integral,\(F(s)\) se definió para\(\text{Re} (s) > 3\), pero la fórmula del residuo se basa en su continuación analítica a\(C - \{3\}\).

La continuación analítica es única

Teorema\(\PageIndex{1}\)

Supongamos que\(f, g\) son analíticos en una región conectada\(A\). Si\(f = g\) en un subconjunto abierto de\(A\) entonces\(f = g\) en todos\(A\).

Prueba

Vamos\(h = f - g\). Por hipótesis\(h (z) = 0\) sobre un conjunto abierto en\(A\). Claramente esto significa que los ceros de no\(h\) están aislados. De vuelta en el Tema 7 mostramos que para analítica\(h\) en una región conectada o\(A\) bien los ceros están aislados o bien\(h\) es idéntico cero encendido\(A\). Así,\(h\) es idénticamente 0, lo que implica\(f = g\) sobre\(A\).

Corolario

Hay a lo sumo una manera de continuar analíticamente una función de una región\(A\) a una región conectada\(B\).

Prueba

Dos continuaciones analíticas estarían de acuerdo\(A\) y por lo tanto deben ser las mismas.

Extensión. Dado que la prueba del teorema utiliza el hecho de que los ceros están aislados, en realidad tenemos la afirmación más fuerte: si\(f\) y de\(g\) acuerdo en un subconjunto no discreto de\(A\) entonces son iguales. En particular, si\(f\) y\(g\) son dos funciones analíticas sobre\(A\) y coinciden en una línea o rayo en\(A\) entonces son iguales.

Aquí hay un ejemplo que muestra por qué necesitamos\(A\) estar conectados en Teorema\(\PageIndex{1}\).

Ejemplo\(\PageIndex{2}\)

Supongamos que\(A\) es el plano menos el eje real. Defina dos funciones de la\(A\) siguiente manera.

\[f(z) = \begin{cases} 1 \text{ for } z \text{ in the upper half-plane} \\ 0 \text{ for } z \text{ in the lower half-plane} \end{cases} \nonumber\]

\[g(z) = \begin{cases} 1 \text{ for } z \text{ in the upper half-plane} \\ 1 \text{ for } z \text{ in the lower half-plane} \end{cases} \nonumber\]

Ambos\(f\) y\(g\) son analíticos\(A\) y coinciden en un conjunto abierto (el medio plano superior), pero no son la misma función.

Aquí un ejemplo que demuestra que se debe tener un poco de cuidado al aplicar el corolario.

Ejemplo\(\PageIndex{3}\)

Supongamos que definimos\(f\) y\(g\) como sigue

\[f(z) = \log (z) \text{ with } 0 < \theta < 2\pi \nonumber\]

\[g(z) = \log (z) \text{ with } -\pi < \theta < \pi \nonumber\]

Claramente\(f\) y de\(g\) acuerdo en el primer cuadrante. Pero no podemos usar el teorema para concluir eso\(f = g\) en todas partes. El problema es que las regiones donde se definen son diferentes. \(f\)se define en\(C\) menos el eje real positivo, y\(g\) se define en\(C\) menos el eje real negativo. La región donde ambos están definidos es\(C\) menos el eje real, que no está conectado.

Debido a que ambos están definidos en el medio plano superior, podemos concluir que ahí son los mismos. (Es fácil ver que esto es cierto.) Pero (en este caso) ser iguales en el primer cuadrante no implica que sean iguales en el medio plano inferior.