4.3: Optimización

Las derivadas parciales nos dicen algo sobre dónde una superficie tiene máximos y mínimos locales. Recuerde que incluso en los casos de una variable, hubo puntos críticos que no eran ni máximos ni mínimos, esto también es cierto para funciones de muchas variables. De hecho, como cabría esperar, la situación es aún más complicada.

Segundas Derivadas

Cuando encuentras una derivada parcial de una función de dos variables, obtienes otra función de dos variables — también puedes tomar sus derivadas parciales. Ya hemos hecho esto antes, en la configuración de una variable. En el ajuste de una variable, la segunda derivada dio información sobre cómo se curvaba la gráfica. En el ajuste de dos variables, las segundas derivadas parciales dan cierta información sobre cómo se curva la superficie, a medida que viaja en secciones transversales, pero esa no es información muy completa sobre toda la superficie.

Imagina que tienes una superficie que está revuelta alrededor de un punto, como lo que sucede cerca de un botón en un sofá sobrerelleno, o un trozo de tela pellizcado, o la piel arrugada cerca de tu pulgar cuando haces un puño. Justo en ese punto, cada dirección que te muevas, sucederá algo diferente —podría aumentar, disminuir, curvar hacia arriba, curvar hacia abajo... Una frase simple como cóncava hacia arriba o cóncava hacia abajo no puede describir todas las cosas que pueden suceder en una superficie.

Sorprendentemente, sin embargo, todavía hay una segunda prueba derivada que puede ayudarte a decidir si un punto es un máximo local o mínimo o ninguno, así que todavía queremos encontrar segundas derivadas.

Segunda Derivadas Parciales

Supongamos$f(x,y)$ is a function of two variables. Then it has four segundas derivadas parciales: $$\begin{align*} f_{xx} & = \frac{\partial}{\partial x}\left(f_x\right)=\left(f_x\right)_x & f_{xy} & = \frac{\partial}{\partial y}\left(f_x\right)=\left(f_x\right)_y\\ f_{yx} & = \frac{\partial}{\partial x}\left(f_y\right)=\left(f_y\right)_x & f_{yy} & = \frac{\partial}{\partial y}\left(f_y\right)=\left(f_y\right)_y \end{align*} \nonumber$$ $f_{xy}$ and $f_{yx}$ are called the mixtas (segundas) derivadas parciales de$f$.

La notación Leibniz para las segundas derivadas parciales es un poco confusa, y no la usaremos tan a menudo: $$\begin{align*} f_{xx} & = \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^2 f}{\partial x^2} & f_{xy} & = \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^2 f}{\partial y \partial x}\\ f_{yx} & = \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^2 f}{\partial x \partial y} & f_{yy} & = \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^2 f}{\partial y^2} \end{align*} \nonumber$$

Observe que el orden de las variables para los parciales mixtos va de derecha a izquierda en la notación Leibniz en lugar de izquierda a derecha.

Ejemplo$\PageIndex{1}$

Encuentra las cuatro derivadas parciales de$f(x,y)=x^2-4xy+4y^2$.

Solución

Tenemos que comenzar por encontrar las (primeras) derivadas parciales: $$\begin{align*} f_x(x,y) & = 2x-4y \\ f_y(x,y) & = -4x+8y \end{align*} \nonumber$$

Ahora ya estamos listos para tomar las segundas derivadas parciales: $$\begin{align*} f_{xx}(x,y) & = \frac{\partial}{\partial x}(2x-4y)=2 \\ f_{xy}(x,y) & = \frac{\partial}{\partial y}(2x-4y)=-4 \\ f_{yx}(x,y) & = \frac{\partial}{\partial x}(-4x+8y)=-4 \\ f_{yy}(x,y) & = \frac{\partial}{\partial y}(-4x+8y)=8 \end{align*} \nonumber$$

Podrías haber notado que las dos derivadas parciales mixtas eran iguales en este último ejemplo. Resulta que no es una coincidencia — ¡es un teorema!

Teorema de derivado parcial mixto

Si$f$, $f_x$, $f_y$, $f_{xy}$, and $f_{yx}$ are all continuous (no breaks in their graphs), then $$f_{xy}=f_{yx}. \nonumber$$

De hecho, siempre$f$ y cuando y todas sus derivadas parciales apropiadas sean continuas, los parciales mixtos son iguales aunque sean de orden superior, e incluso si la función tiene más de dos variables.

Este teorema significa que la confusa notación Leibniz para segundas derivadas no es un gran problema —en casi todas las situaciones los parciales mixtos son iguales, por lo que el orden en que los calculamos no importa.

Ejemplo$\PageIndex{2}$

Encuentra$\frac{\partial^2 f}{\partial x \partial y}$ para$f(x,y)=\frac{e^{x+y}}{y^3+y}+y\ln(y)$.

Solución

Ya encontramos las primeras derivadas parciales en un ejemplo anterior: $$\begin{align*} \frac{\partial f}{\partial x} & = \frac{1}{y^3+y}e^{x+y} \\ \frac{\partial f}{\partial y} & = \frac{\left( e^{x+y}(1) \right)\left( y^3+y \right)-\left( e^{x+y} \right)\left( 3y^2+1 \right)}{\left( y^3+y \right)^2}+\left( 1 \right)\left( \ln(y) \right)+\left( y \right)\left( \frac{1}{y} \right) \end{align*} \nonumber$$

Ahora necesitamos encontrar la derivada parcial mixta. El teorema dice eso$\frac{\partial f^2}{\partial x \partial y}=\frac{\partial f^2}{\partial y \partial x}$, por lo que no importa si encontramos la derivada parcial de$\frac{\partial f}{\partial x}$ con respecto a$y$ o la derivada parcial de$\frac{\partial f}{\partial y}$ con respecto a$x$. ¿Cuál preferirías hacer?

Parece que será más fácil calcular el parcial mixto al encontrar la derivada parcial de$\frac{\partial f}{\partial x}= \frac{1}{y^3+y}e^{x+y}$ con respecto a$y$ — todavía se ve desordenado, pero se ve menos desordenado: $$\frac{\partial f^2}{\partial y \partial x}= \frac{\partial}{\partial y}\left(\frac{1}{y^3+y}e^{x+y}\right)=\frac{\left(e^{x+y}\right)\left(y^3+y\right)-\left(e^{x+y}\right)\left(3y^2+1\right)}{\left(y^3+y\right)^2} \nonumber$$

Si hubiéramos decidido hacer esto de otra manera, terminaríamos en el mismo lugar. Eventualmente...

Maxima local, minima local y puntos de sillín

Repasemos brevemente los problemas max-min en una variable.

Un máximo local es un punto en una curva que es más alto que todos los puntos cercanos. Un min local es más bajo que todos los puntos cercanos. Sabemos que el máximo local o el mínimo solo pueden ocurrir en puntos críticos, donde la derivada es cero o indefinida. Pero también sabemos que no todos los puntos críticos son max o min, por lo que también necesitamos probarlos, con la Prueba de Primera Derivada o Segunda Derivada.

La situación con una función de dos variables es muy similar. Así como en el caso de una variable, el primer paso es encontrar puntos críticos, lugares donde ambas derivadas parciales son cero o indefinidas.

Definición: Máximo y Mínimo Local

• $f$tiene un máximo local en$(a, b)$ si$f(a, b) \geq f(x, y)$ para todos los puntos$(x, y)$ cercanos$(a, b)$.
• $f$tiene un mínimo local en$(a, b)$ si$f(a, b) \leq f(x, y)$ para todos los puntos$(x, y)$ cercanos$(a, b)$.

Un punto crítico para una función$f(x, y)$ es un punto$(x, y)$ (o$(x, y, f(x, y))$) donde ambos son ciertos los siguientes:

1. $f_x=0$o no está definido, y
2. $f_y=0$o no está definido.

Al igual que en el caso de una variable, un máximo o mínimo local de solo$f$ puede ocurrir en un punto crítico.

Al igual que en la configuración de una variable, no todos los puntos críticos son locales max o min. Para una función de dos variables, el punto crítico podría ser un máximo local, un mínimo local o un punto de sillín.

Un punto en una superficie es un máximo local si es más alto que todos los puntos cercanos; un punto es un mínimo local si es menor que todos los puntos cercanos.

Un punto de sillín es un punto en una superficie que es mínimo a lo largo de algunos caminos y un máximo a lo largo de algunos otros. Se llama así porque tiene la forma un poco como una silla de montar que podrías usar para montar a caballo. Puedes ver una punta de silla haciendo un puño —entre los nudillos de tus dedos índice y medio, puedes ver un lugar que es mínimo a medida que vas atravesando tus nudillos, pero un máximo a medida que avanzas por tu mano hacia tus dedos.

Aquí hay una imagen de un punto de silla de montar desde algunos ángulos diferentes. Esta es la superficie$f(x,y)=5x^2-3y^2+10$, y hay un punto de sillín por encima del origen. Las líneas muestran cómo se ve la superficie por encima de los ejes$x$$y$ - y -. Observe cómo el punto por encima del origen, donde se cruzan las líneas, es un mínimo local en una dirección, pero un máximo local en la otra dirección.

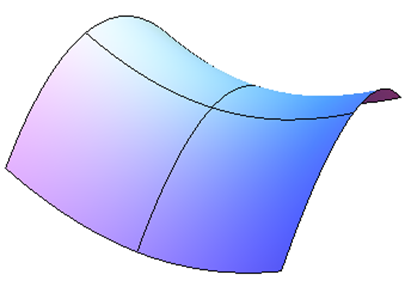
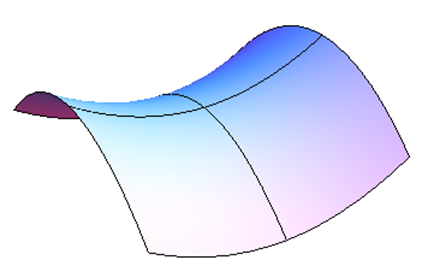
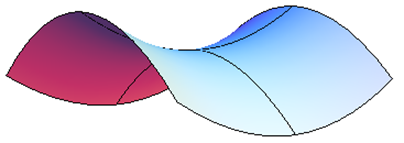
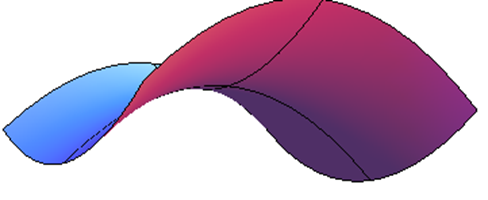
Segunda Prueba Derivada

Al igual que en el caso de una variable, necesitaremos una forma de probar puntos críticos para ver si son locales max o min. Hay una segunda prueba derivada para funciones de dos variables que pueden ayudar, pero, al igual que en el caso de una variable, no siempre dará respuesta.

La Segunda Prueba Derivada para Funciones de Dos Variables

1. Encuentra todos los puntos críticos de$f(x,y)$.
2. Calcular $$D(x,y)=\left(f_{xx}\right)\left(f_{yy}\right)-\left(f_{xy}\right)\left(f_{yx}\right),\nonumber$$ y evaluarlo en cada punto crítico.
   1. Si$D \gt 0$, entonces$f$ tiene un máximo local o mínimo en el punto crítico. Para ver cuál, mira el signo de$f_{xx}$:
      • Si$f_{xx}\gt 0$, entonces$f$ tiene un mínimo local en el punto crítico.
      • Si$f_{xx}\lt 0$, entonces$f$ tiene un máximo local en el punto crítico.
   2. Si$D \lt 0$ entonces$f$ tiene un punto de sillín en el punto crítico.
   3. Si$D = 0$, podría haber un máximo local, mínimo local, o ninguno (es decir, la prueba en inconcluso).

Ejemplo$\PageIndex{3}$

Encuentra todos los máximos, mínimos y puntos de sillín locales para la función $$f(x,y)=x^3+y^3+3x^2-3y^2-8. \nonumber$$

Solución

Primero necesitamos las derivadas parciales:$f_x=3x^2+6x$ y$f_y=3y^2-6y$.

Los puntos críticos son los lugares donde ambos son cero (ninguno es nunca indefinido):$f_x=3x^2+6x=3x(x+2)=0$ cuándo$x = 0$ o cuándo$x = -2$. $f_y=3y^2-6y=3y(y-2)=0$cuándo$y = 0$ o cuándo$y = 2$.

Armando estos, obtenemos cuatro puntos críticos: (0, 0), (-2, 0), (0, 2) y (-2, 2).

Ahora para clasificarlos, usaremos la Prueba de Segunda Derivada. Necesitaremos todas las segundas derivadas parciales: $$f_{xx}=6x+6,\ f_{yy}=6y-6,\ f_{xy}=f_{yx}=0.\nonumber$$

Entonces $$D(x,y)=(6x+6)(6y-6)-(0)(0)=(6x+6)(6y-6). \nonumber$$

Ahora mira cada punto crítico a su vez:

• En (0, 0):$D(0,0)=(6(0)+6)(6(0)-6)=(6)(-6)=-36 \lt 0$, por lo que hay un punto de sillín en (0, 0).
• En (-2, 0):$D(-2,0)=(6(-2)+6)(6(0)-6)=(-6)(-6)=36 \gt 0$ y$f_{xx}(-2,0)=6(-2)+6=-6 \lt 0$, por lo que hay un máximo local en (-2, 0).
• En (0, 2):$D(0,2)=(6(0)+6)(6(2)-6)=(6)(6)=36 \gt 0$ y$f_{xx}(0,2)=6(0)+6=6 \gt 0$, por lo que hay un mínimo local en (0, 2).
• En (-2, 2):$D(-2,2)=(6(-2)+6)(6(2)-6)=(-6)(6)=-36 \lt 0$, por lo que hay otro punto de sillín en (-2, 2).

Ejemplo$\PageIndex{4}$

Encuentra todos los máximos, mínimos y puntos de sillín locales para la función $$z=9x^3+\frac{y^3}{3}-4xy. \nonumber$$

Solución

Necesitaremos todas las derivadas parciales y las segundas derivadas parciales, así que vamos a calcularlas todas primero: $$\begin{align*} z_x & = 27x^2-4y,\quad z_y= y^2-4x,\\ z_{xx} & = 54x,\quad z_{xy}=z_{yx}= -4,\quad z_{y}= 2y. \end{align*} \nonumber$$

Ahora para encontrar los puntos críticos: Necesitamos ambos$z_x$ y$z_y$ ser cero (ninguno es nunca indefinido), así que necesitamos resolver este conjunto de ecuaciones simultáneamente: $$\begin{align*} z_x & = 27x^2-4y=0 \\ z_y & = y^2-4x=0 \end{align*} \nonumber$$

Quizás ha pasado un tiempo desde que resolviste sistemas de ecuaciones. Un método de solución es el método de sustitución — resolver una ecuación para una variable y sustituir en la otra ecuación:\[ \left.\begin{align*} 27x^2-4y & = 0 \\ y^2-4x & = 0 \end{align*}\right\} \to \text{Solve $y^2-4x=0$ for $x=\frac{y^2}{4}$ $\dots$} \nonumber \]... luego sustituir en la otra ecuación: $$\begin{align*} 27\left(\frac{y^2}{4}\right)^2-4y & = 0 \\ \frac{27}{16}y^4-y & = 0 \end{align*} \nonumber$$

Ahora solo tenemos una ecuación en una variable que resolver. Factorizando un$y$ da $$y\left(\frac{27}{16}y^3-1\right)=0, \nonumber$$ así$y=0$ o$\frac{27}{16}y^3-1=0$, dando$y=\sqrt[3]{\frac{1}{27/16}}=\frac{\sqrt[3]{4}}{3}$.

Conectarse de nuevo a la ecuación$x=\frac{y^2}{4}$ para encontrar nos$x$ da los dos puntos críticos: (0,0) y$\left(\frac{4}{9},\frac{4}{3}\right)$.

Ahora para probarlos. Primero computar $$\begin{align*} D(x,y) & = (f_{xx})(f_{yy})-(f_{xy})(f_{yx}) \\ & = (54x)(2y)-(-4)(-4) \\ & = 108xy-16 \end{align*} \nonumber$$ Luego evaluar$D$ en los dos puntos críticos:

• A (0,0):$D(0,0) = -16 \lt 0$, por lo que hay un punto de sillín en (0, 0).
• En$\left(\frac{4}{9},\frac{\sqrt[3]{4}}{3}\right)$:$D\left(\frac{4}{9},\frac{\sqrt[3]{4}}{3}\right) =16(\sqrt[3]{4}-1) \gt 0$, y$f_{xx}\left(\frac{4}{9},\frac{\sqrt[3]{4}}{3}\right) \gt 0$, entonces hay un mínimo local en$\left(\frac{4}{9},\frac{\sqrt[3]{4}}{3}\right)$.

Optimización Aplicada

Ejemplo$\PageIndex{5}$

Una empresa fabrica dos productos. A continuación se dan las ecuaciones de demanda para los dos productos. $p_1$,$p_2$$q_1$, y$q_2$ son los precios y cantidades de los Productos 1 y 2. $$\begin{align*} q_1 & = 200-3p_1-p_2 \\ q_2 & = 150-p_1-2p_2 \end{align*} \nonumber$$

Solución

Encuentre el precio que la compañía debe cobrar por cada producto para maximizar los ingresos totales. ¿Cuál es ese ingreso máximo?

Los ingresos siguen siendo$\cdot$ cantidad de precio. Si vendemos dos productos, los ingresos totales serán la suma de los ingresos de los dos productos: $$\begin{align*} R(p_1,p_2) & = p_1q_1+p_2q_2 \\ & = p_1(200-3p_1-p_2)+p_2(150-p_1-2p_2) \\ & = 200p_1-3p_1^2-2p_1p_2+150p_2-2p_2^2 \end{align*} \nonumber$$

Esto es una función de dos variables, los dos precios, y necesitamos optimizarlo (igual que en los ejemplos anteriores). Primero encontramos puntos críticos. La notación aquí se vuelve un poco difícil de ver, pero aguanta ahí — esto es lo mismo que hemos hecho antes. $$R_{p_1}=200-6p_1-2p_2 \ \text{ and } \ R_{p_2}=150-2p_1-4p_2. \nonumber$$

Resolver estos simultáneamente da el punto crítico$(p_1, p_2)=(25,25)$

Para confirmar que esto da ingresos máximos, necesitamos usar la Prueba de Segunda Derivada. Encuentra todas las segundas derivadas: $$R_{p_1 p_2}=-6,\ R_{p_2 p_2}=-4,\ \text{ and }\ R_{p_1 p_2}=R_{p_2 p_1}=-2. \nonumber$$

Entonces$D(25,25)=(-6)(-4)-(-2)(-2) \gt 0$ y$R_{p_1 p_2}(25,25) \lt 0$, entonces esto realmente es un máximo local.

Así, para maximizar los ingresos la compañía debería cobrar $25 por unidad por ambos productos. Esto arrojará un ingreso máximo de $4375.