5.6: Tareas escolares- Comprensión de ecuaciones diferenciales
- Page ID
- 116892
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
- Para cada ecuación diferencial a continuación, realice los siguientes pasos.
- Describir lo que mide cada variable o función (si es posible en esta etapa), y dar las unidades correctas.
- Describa lo que dice la ecuación. Use frases como “Si tal y tal es grande, que tal y tal crece más rápido”.
- Explique por qué las relaciones de la viñeta anterior tienen sentido en términos de la historia o situación física.
- Dejar\(T(t)\) ser la temperatura de un objeto de enfriamiento en grados Celsius, y dejar que\(t\) se mida en segundos. La ley de Newton del estado de enfriamiento que\(T'(t) = -k(T(t) - T_{\text{air}})\). Aquí\(T_{\text{air}}\) está la temperatura del aire ambiente.
- \(H(t)\)Sea la altura de una montaña medida en metros durante un largo periodo de tiempo (\(t\)medida en millones de años). Supongamos\(H(t)\) que satisface la ecuación diferencial
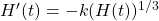 .
. - Dejar\(y(t)\) que la población de peces en un lago sea cosechada a tasa de\(H\) peces por año. Supongamos\(y(t)\) que satisface la ecuación diferencial
\(y'(t) = k y(t) - (m + c y(t)) y(t) - H\). Aquí,\(k y(t)\) representa la tasa de natalidad,\((m + cy(t)) y(t)\) la tasa de mortalidad natural y\(H\) la tasa de cosecha.
- Deshojear el artículo “Beber en campus: un modelo epidemiológico” de J. L. Manthey, A. Y. Aidoo & K. Y. Ward. No vas a entender todo el artículo — ¡está bien! Pero tratemos de averiguar partes y pedazos de ella.
Aquí está su primera ecuación diferencial a partir de la secion 2 del artículo.
\[\[\frac{dN}{dt} = \eta - \eta N - \alpha N P + \beta S + \epsilon P\]\]
- ¿Qué representan las variables N, S y P?
- En la primera ecuación diferencial, ¿qué términos representan a los estudiantes universitarios en transición a beber más? ¿Cuál representa a los estudiantes universitarios en transición a beber menos?
- ¿Cuál es una conclusión principal del artículo?


