1.6: Combinatoria y Optimización
- Page ID
- 118255
Es probable que ya te hayan introducido problemas de optimización, ya que los estudiantes de cálculo de todo el mundo están familiarizados con la difícil situación de los agricultores que intentan cercar la mayor superficie de tierra dada una cierta cantidad de cerco o personas que necesitan cruzar ríos río abajo de su ubicación actual que deben decidir dónde deben cruzar en base a la velocidad a la que puedan correr y nadar. Sin embargo, estos problemas son inherentemente continuos. En teoría, puedes cruzar el río en cualquier punto que quieras, aunque fuera irracional. (OK, entonces no es exactamente irracional, sino una buena aproximación decimal.) En este curso, examinaremos algunos problemas de optimización que no son continuos, ya que solo los valores enteros para las variables tendrán sentido. Resulta que muchos de estos problemas son muy difíciles de resolver en general.
En la Figura 1.18, usamos letras para las etiquetas en los vértices para ayudar a distinguir visualmente de los pesos enteros en los bordes.
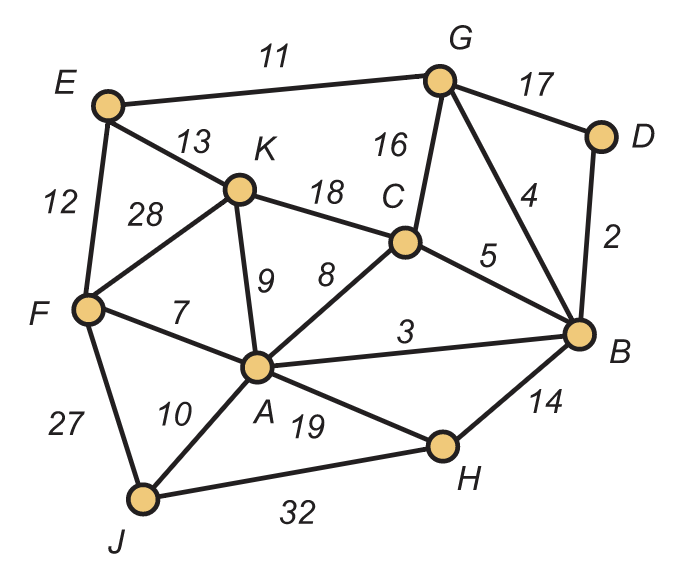
Figura 1.18. Un gráfico etiquetado con bordes ponderados
Supongamos que los vértices son ciudades, los bordes son carreteras y los pesos en los bordes representan la distancia.
- ¿Cuál es el camino más corto de vértice\(E\) a vértice\(B\)?
- Supongamos que Ariel es un vendedor cuya base de operaciones es la ciudad\(A\). ¿En qué orden debe Ariel visitar las otras ciudades para que pase por cada una de ellas al menos una vez y regrese a casa al final, manteniendo al mínimo la distancia total recorrida? ¿Puede Ariel realizar tal recorrido visitando cada ciudad exactamente una vez?
- Sanjay es ingeniero de inspección de carreteras y debe atravesar todas las autopistas cada mes. La base de Sanjay es City\(E\). ¿En qué orden debería Sanjay atravesar las autopistas para minimizar la distancia total recorrida? ¿Puede Sanjay hacer tal recorrido viajando por cada autopista exactamente una vez?
Ahora supongamos que los vértices son ubicaciones de sucursales bancarias en Atlanta y que los pesos en una arista representan el costo, en millones de dólares, de construir un enlace de datos de alta capacidad entre las sucursales bancarias en sus dos puntos finales. En este modelo, si no hay borde entre dos sucursales, significa que el costo de construir un enlace de datos entre este par en particular es prohibitivamente alto (aquí podríamos estar tentados a decir que el costo es infinito, pero los autores no admiten conocer el significado de esta palabra).
Nuestro reto es decidir qué enlaces de datos deben construirse para formar una red en la que cualquier sucursal bancaria pueda comunicarse con cualquier otra sucursal. Suponemos que los datos pueden fluir en cualquier dirección en un enlace, en caso de que se construyan, y que los datos se pueden retransmitir a través de cualquier número de enlaces de datos. Entonces, para permitir una comunicación completa, deberíamos construir un árbol de expansión en esta red. En la Figura 1.20, se muestra una gráfica a\(G\) la izquierda y uno de sus muchos árboles de expansión a la derecha.
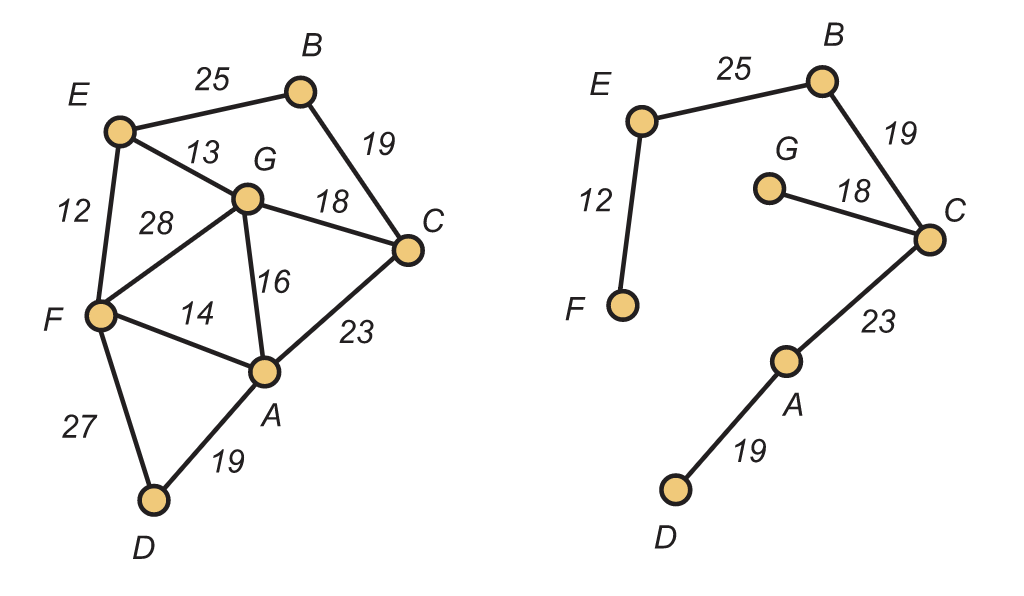
Figura 1.20. Un gráfico ponderado y un árbol de expansión
El peso del árbol de expansión es la suma de los pesos en los bordes. En nuestro modelo, esto representa los costos, nuevamente en millones de dólares, de construir los enlaces de datos asociados con los bordes en el árbol de expansión. Para el árbol de expansión que se muestra en la Figura 1.20, este total es
\(12 + 25 + 19 + 18 + 23 + 19 = 116\).
De todos los árboles que atraviesan, al banco naturalmente le gustaría encontrar uno que tenga un peso mínimo.
¿Cuántos árboles de expansión tiene esta gráfica? Para una gráfica grande, digamos una con\(2875\) vértices, ¿tiene sentido encontrar todos los árboles de expansión y simplemente tomar el de costo mínimo? En particular, para un entero positivo\(n\), ¿cuántos árboles tienen establecido vértices\(\{1,2,3,...,n\}\)?


