2.4: Pruebas combinatorias
- Page ID
- 118286
Los argumentos combinatorios se encuentran entre los más bellos de todas las matemáticas. A menudo, las declaraciones que pueden probarse por otros métodos más complicados (generalmente involucran grandes cantidades de tediosas manipulaciones algebraicas) tienen pruebas muy cortas una vez que se puede hacer una conexión con el conteo. En esta sección, presentamos una nueva forma de pensar sobre los problemas combinatorios con varios ejemplos. Nuestro objetivo es ayudarle a desarrollar un “presentimiento” para problemas combinatorios.
Dejar\(n\) ser un entero positivo. Utilice la Figura 2.14 para explicar por qué
\(1+2+3+\cdot \cdot \cdot + n = \frac{n(n+1)}{2}\).
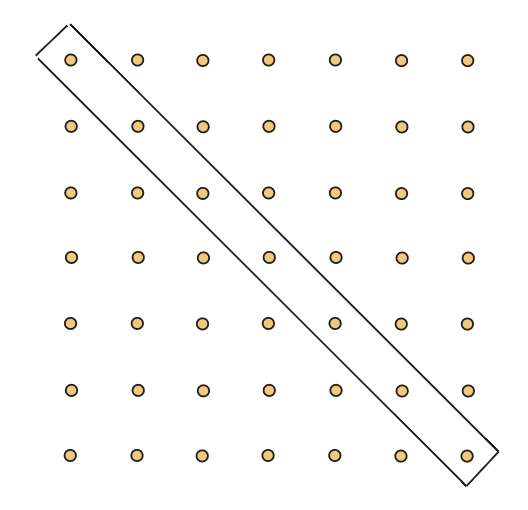
- Figura 2.14: La suma de los primeros\(n\) enteros
- Solución
-
Considere una\((n+1) \times (n+1)\) matriz de puntos como se representa en la Figura 2.14. Hay\((n+1)^2\) puntos en conjunto, con exactamente\(n+1\) en la diagonal principal. Las entradas fuera de la diagonal se dividen naturalmente en dos partes de igual tamaño, las de arriba y las de abajo de la diagonal.
Además, cada una de esas dos partes tiene\(S(n) = 1+2+3+\cdot \cdot \cdot+n\) puntos. De ello se deduce que
\(S(n) = \frac{(n+1)^2-(n+1)}{2}\)
¡y esto es obvio! Ahora un poco de álgebra en el lado derecho de esta expresión produce la fórmula dada anteriormente.
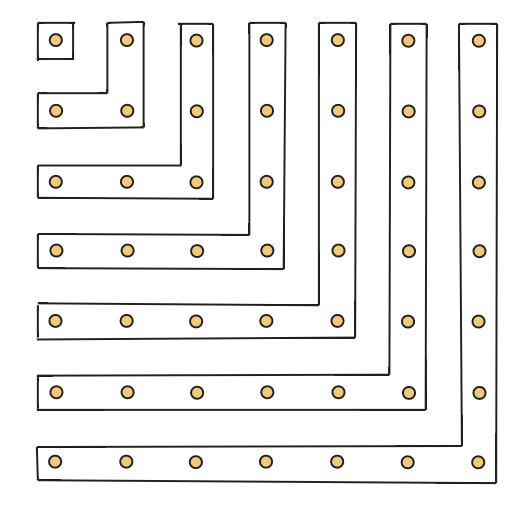
Dejar\(n\) ser un entero positivo. Explicar por qué
\(1+3+5+\cdot \cdot \cdot+2n-1 = n^2\)
- Solución
-
El lado izquierdo es solo la suma de los primeros enteros\(n\) impares. Pero como se sugiere en la Figura 2.16, esto es claramente igual a\(n^2\).
Dejar\(n\) ser un entero positivo. Explicar por qué
\(\dbinom{n}{0}+\dbinom{n}{1}+\dbinom{n}{2}+\cdot \cdot \cdot+\dbinom{n}{n} = 2^n\).
- Solución
-
Ambos lados cuentan el número de cadenas de bits de longitud\(n\), con el lado izquierdo primero agrupándolas según el número de 0's.
Dejar\(n\) y\(k\) ser enteros con\(0 \leq k \leq n\). Explicar por qué
\(\dbinom{n}{k+1} = \dbinom{k}{k} + \dbinom{k+1}{k} + \dbinom{k+2}{k} + \cdot \cdot \cdot +\dbinom{n-1}{k}\).
- Solución
-
Para probar esta fórmula, simplemente observamos que ambos lados cuentan el número de cadenas de bits de longitud\(n\) que contienen\(k+1\) 1's con el lado derecho primero particionándolos de acuerdo a la última ocurrencia de un 1. (Por ejemplo, si el último 1 ocurre en posición\(k+5\), entonces los\(k\) 1 restantes deben aparecer en las\(k+4\) posiciones anteriores, dando\(C(k+4,k)\) cadenas de este tipo). Tenga en cuenta que cuando\(k=1\) (so\(k+1=2\)), tenemos la misma fórmula que se desarrolló anteriormente para la suma de los primeros enteros\(n\) positivos.
Explicar la identidad
\(3^n = \dbinom{n}{0}2^0 + \dbinom{n}{1}2^1 + \dbinom{n}{2}2^2+ \cdot \cdot \cdot +\dbinom{n}{n}2^n\).
- Solución
-
Ambos lados cuentan el número de\(\{0,1,2\}\) -cuerdas de longitud\(n\), el lado derecho primero particionándolas de acuerdo a posiciones en la cuerda que no son 2. (Por ejemplo, si 6 de las posiciones no son 2, primero debemos elegir esas 6 posiciones de\(C(n,6)\) maneras y luego hay\(2^6\) formas de llenar esas seis posiciones eligiendo un 0 o un 1 para cada posición.)
Explicar por qué, para cada entero no negativo\(n\),
\(\dbinom{2n}{n} = \dbinom{n}{0}^2 + \dbinom{n}{1}^2 + \dbinom{n}{2}^2 + \cdot \cdot \cdot +\dbinom{n}{n}^2\).
- Solución
-
Ambos lados cuentan el número de cadenas de bits de longitud\(2n\) con la mitad de los bits siendo 0's, con el lado derecho primero particionándolos de acuerdo con el número de 1's que ocurren en las primeras\(n\) posiciones de la cadena. Tenga en cuenta que también estamos utilizando la identidad trivial\(\binom{n}{k} = \binom{n}{n-k}\).