2.5: La naturaleza ubicua de los coeficientes binomiales
- Page ID
- 118298
En esta sección, presentamos varios problemas combinatorios que pueden resolverse apelando a los coeficientes binomiales, aunque a primera vista, no parecen tener nada que ver con conjuntos.
El auxiliar de oficina está distribuyendo suministros. ¿De cuántas formas puede distribuir 18 carpetas idénticas entre cuatro empleados de oficina: Audrey, Bart, Cecilia y Darren, con la restricción adicional de que cada uno recibirá al menos una carpeta? Imagina las carpetas colocadas en fila. Entonces hay 17 brechas entre ellas. De estas brechas, elige tres y coloca un divisor en cada una. Entonces esta elección divide las carpetas en cuatro conjuntos no vacíos. El primero va para Audrey, el segundo para Bart, etc. Así la respuesta es\(C(17,3)\). En la Figura 2.22, ilustramos este esquema con Audrey recibiendo 6 carpetas, Bart obteniendo 1, Cecilia 4 y Darren 7.

Supongamos que rehacemos el problema anterior pero bajamos la restricción de que cada uno de los cuatro empleados obtiene al menos una carpeta. Ahora, ¿de cuántas formas se puede hacer la distribución?
- Solución
-
La solución implica una especie de “truco”. Primero, convertimos el problema en uno que ya sabemos resolver. Esto se logra inflando artificialmente la asignación de todos por uno. Es decir, si Bart obtendrá 7 carpetas, decimos que obtendrá 8. También, inflar artificialmente el número de carpetas en 4, una por cada una de las cuatro personas. Entonces ahora imagina una fila de\(22 = 18 + 4\) carpetas. Nuevamente, elige 3 brechas. Esto determina una asignación distinta de cero para cada persona. La asignación real es una menos y puede ser cero. Entonces la respuesta es\(C(21,3)\).
Nuevamente tenemos el mismo problema que antes, pero ahora queremos contar el número de distribuciones donde solo Audrey y Cecilia tienen la garantía de obtener una carpeta. A Bart y Darren se les permite obtener cero carpetas. Ahora el truco es inflar artificialmente la asignación de Bart y Darren, pero dejar los números para Audrey y Cecilia como están. Entonces la respuesta es\(C(19,3)\).
Aquí hay una reformulación de la discusión anterior expresada en términos de soluciones enteras de desigualdades.
Contamos el número de soluciones enteras a la desigualdad
\(x_1+x_2+x_3+x_4+x_5+x_6 \leq 538\)
sujeto a diversos conjuntos de restricciones sobre los valores de\(x_1,x_2,...,x_6\). Algunas de estas restricciones requerirán que la desigualdad en realidad sea una ecuación.
El número de soluciones enteras es:
- \(C(537,5)\), cuando todos\(x_i > 0\) y la igualdad se mantiene
- \(C(543,5)\), cuando todos\(x_i \geq 0\) y la igualdad se mantiene
- \(C(291,3)\), cuando\(x_1,x_2,x_4,x_6 > 0\),,\(x_3 = 52\)\(x_5 = 194\), y la igualdad se mantiene
- \(C(537,6)\), cuando todo\(x_i > 0\) y la desigualdad es estricta (Imagínese una nueva variable\(x_7\) que es el equilibrio. Tenga en cuenta que\(x_7\) debe ser positivo.)
- \(C(543,6)\), cuando todo\(x_i \geq 0\) y la desigualdad es estricta (Agregar una nueva variable\(x_7\) como arriba. Ahora es el único que se requiere para ser positivo.)
- \(C(544,6)\), cuando todos\(x_i \geq 0\).
Un problema clásico de enumeración (con conexiones a varios problemas) implica contar caminos de celosía. Una ruta de celosía en el plano es una secuencia de pares ordenados de números enteros:
\((m_1,n_1),(m_2,n_2),(m_3,n_3),...,(m_t,n_t)\)
para que para todos\(i = 1,2,...t-1\), ya sea
- \(m_{i+1} = m_i + 1\)y\(n_{i+1} = n_i\), o
- \(m_{i+1} = m_i\)y\(n_{i+1} = n_i + 1\).
En la Figura 2.26, se muestra una trayectoria de celosía de (0,0) a (13,8).
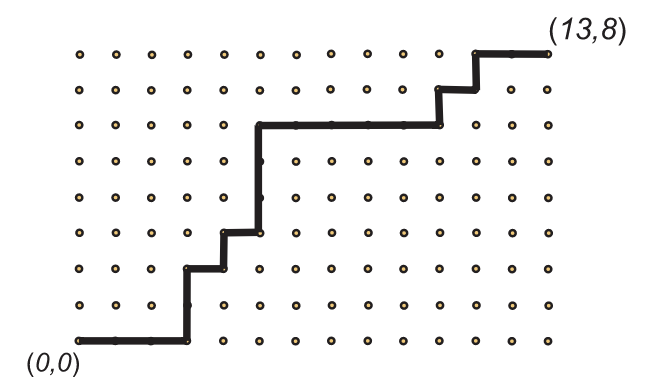
El número de caminos de celosía de\((m,n)\) a\((p,q)\) es\(C((p-m) + (q-n),p-m)\).
Para ver por qué esta fórmula es válida, tenga en cuenta que una ruta de celosía es solo una\(X\) -string con\(X=\{H,V\}\), donde\(H\) significa horizontal y\(V\) significa vertical. En este caso, hay exactamente\((p−m)+(q−n)\) movimientos, de los cuales\(p−m\) son horizontales.
Dejar\(n\) ser un entero no negativo. Entonces el número de caminos de celosía desde\((0,0)\) los\((n,n)\) que nunca van por encima de la línea diagonal\(y=x\) es el número catalán
\(C(n) = \frac{1}{n+1} \dbinom{2n}{n}\).
Para ver que esta fórmula se sostiene, considere la familia\(\mathcal{P}\) de todos los caminos de celosía desde\((0,0)\) hasta\((n,n)\). Una ruta de celosía de\((0,0)\) a\((n,n)\) es solo una\(\{H,V\}\) =cadena de longitud\(2n\) con\(n\)\(H\) exactamente. entonces\(|\mathcal{P}| = \binom{2n}{n}\). Clasificamos los caminos en\(\mathcal{P}\) como buenos si nunca pasan por encima de la diagonal; de lo contrario, son malos. Una cadena\(s \in \mathcal{P}\) es buena si el número de\(V\)'s en un segmento inicial de\(s\) nunca excede el número de s.\(H\) Por ejemplo, la cadena "\(HHVHVVHHHVHVVV\)" es una buena ruta de celosía de\((0,0)\) a\((7,7)\), mientras que la ruta "\(HVHVHHVVVHVHHV\)" es mala. En el segundo caso, tenga en cuenta que después de 9 movimientos, tenemos\(V\) 5's y\(H\) 4's.
Dejar\(\mathcal{G}\) y\(\mathcal{B}\) denotar la familia de todos los caminos buenos y malos, respectivamente. Por supuesto, nuestro objetivo es determinar\(|\mathcal{G}|\).
Considera un camino\(s \in \mathcal{B}\). Entonces hay un mínimo entero\(i\) para que\(s\) tenga más\(V\)'s que\(H\)'s en las primeras\(i\) posiciones. Por la minimalidad de\(i\), es fácil ver que\(i\) debe ser extraño (de lo contrario, podemos retroceder un escalón), y si establecemos\(i = 2j +1\), entonces en las primeras\(2j+1\) posiciones de\(s\), hay exactamente\(j\)\(H\)\(j+1\)\(V\)'s y's.\(2n-2j-1\) posiciones (la “cola de\(s\) “) tienen\(n-j\)\(H\)'s y\(n-j-1\)\(V\)'s. Ahora nos\(s\) transformamos en una nueva cuerda\(s\) 'reemplazando los\(H\)'s en la cola de\(s\) por\(V\) y los\(V\)'s en la cola de\(s\) by\(H\) y dejando sin cambios\(2j+1\) las posiciones iniciales. Por ejemplo, véase la Figura 2.29, donde el camino\(s\) se muestra sólido y\(s\) ′ concuerda con\(s\) hasta que cruza la línea\(y=x\) y luego es el camino discontinuo. Entonces\(s\) ′ es una cadena de longitud\(2n\) que tiene\((n−j)+(j+1)=n+1\)\(V\)'s y\((n−j−1)+j=n−1\)\(H\)'s, así que\(s\) ′ es un camino de celosía de\((0,0)\) a\((n−1,n+1)\). Tenga en cuenta que existen\(\binom{2n}{n-1}\) tales caminos de celosía.
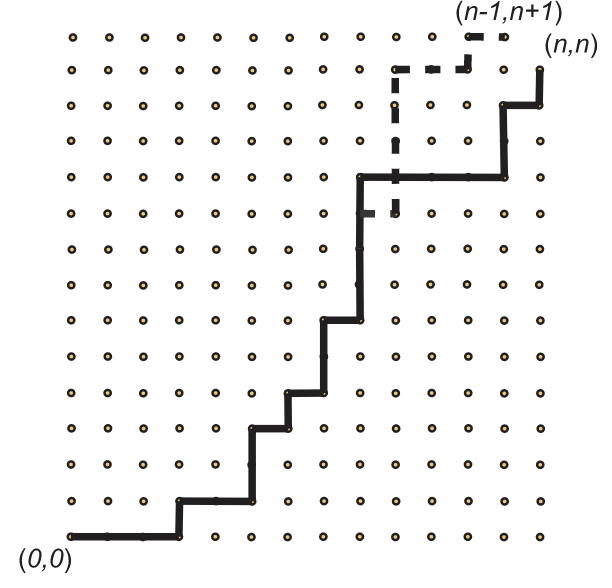
También podemos observar que la transformación que hemos descrito es de hecho una biyección entre\(\mathcal{B}\) y\(\mathcal{P}\) ', el conjunto de caminos de celosía de\((0,0)\) a\((n-1, n+1)\). Para ver que esto es cierto, tenga en cuenta que cada camino\(s\)\(\mathcal{P}\) ′ in ′ debe cruzar la línea\(y=x\), así que hay una primera vez que la cruza, digamos en posición\(i\). Nuevamente,\(i\) debe ser extraño, así\(i=2j+1\) y hay\(j\)\(H\)'s y\(j+1\)\(V\)'s en las primeras\(i\) posiciones de\(s\) '. Por lo tanto, la cola de\(s\) 'contiene\(n+1-(j+1)=n-j\)\(V\)\((n-1)-j\)\(H\)'s y's, así que intercambiando\(H\)\(V\)'s y's en la cola de\(s\)' crea una nueva cadena\(s\) que tiene\(n\)\(H\)'s y\(n\)\(V\)'s y por lo tanto representa una camino de celosía de (0,0) a\((n,n)\), pero sigue siendo un camino de celosía malo, ya que no ajustamos la primera parte del camino, lo que resulta en cruzar la línea\(y=x\) en posición\(i\). Por lo tanto,\(|\mathcal{B}| = |\mathcal{P}'|\) y así
\(C(n) = |\mathcal{G}| = |\mathcal{P}| - |\mathcal{B}| = |\mathcal{P}| - |\mathcal{P}'| = \dbinom{2n}{n} - \dbinom{2n}{n-1} = \frac{1}{n+1}\dbinom{2n}{n}\),
después de un poco de álgebra.
Vale la pena observar que en el Ejemplo 2.28, hicimos uso de dos técnicas enumerativas comunes: dar una biyección entre dos clases de objetos, una de las cuales es “más fácil” de contar que la otra, y contar los objetos que no deseamos enumerar y deducir sus número del total.


