2.3: Gráfica y Árboles
- Page ID
- 112679
2.3.1: Gráficas no dirigidas
En la Sección 1.3.4 se introdujo la idea de una gráfica dirigida. Las gráficas constan de vértices y aristas. Describimos vértices y aristas de la misma manera que describimos puntos y líneas en geometría: en realidad no decimos qué son los vértices y aristas, sino que decimos lo que hacen. Simplemente no tenemos un sistema de axiomas complicado como lo hacemos en geometría. Un gráfico consiste en un conjunto\(V\) llamado conjunto de vértices y un conjunto\(E\) llamado conjunto de bordes. Cada miembro de\(V\) se llama vértice y cada miembro de\(E\) se llama borde. Asociados a cada borde hay dos vértices (no necesariamente diferentes) llamados sus puntos finales. Dibujamos imágenes de gráficas dibujando puntos para representar los vértices y segmentos de línea (curvos si lo elegimos) cuyos extremos están en vértices para representar los bordes. En la Figura 2.3.1 mostramos tres imágenes de gráficas.
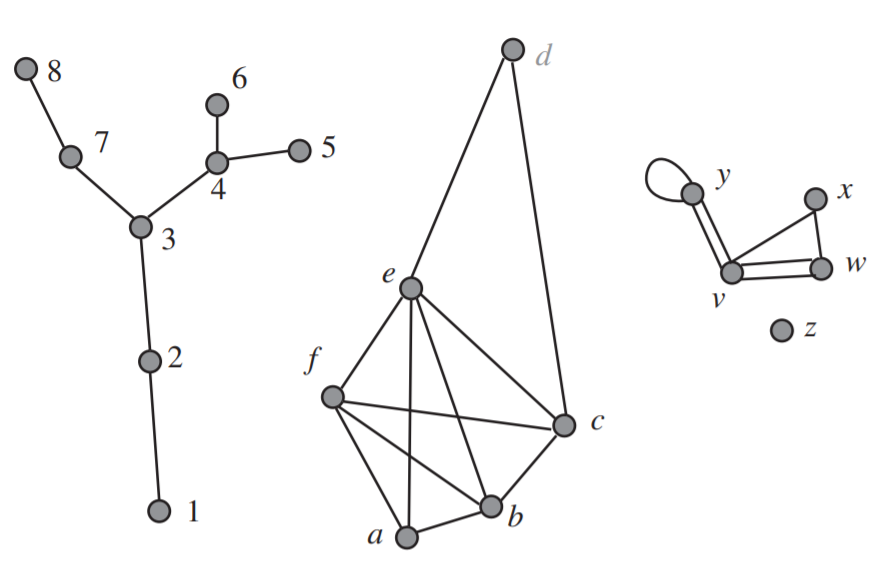
Cada círculo gris de la figura representa un vértice; cada segmento de línea representa un borde. Notarás que etiquetamos los vértices; estas etiquetas son nombres que elegimos para dar los vértices. Podemos elegir nombres o no como nos plazca. La tercera gráfica también muestra que es posible tener un borde que conecte un vértice (como el etiquetado\(y\)) consigo mismo o es posible tener dos o más aristas (como las que están entre vértices\(v\) y\(y\)) entre dos vértices. El grado de un vértice es el número de veces que aparece como punto final de aristas; así el grado de\(y\) en la tercera gráfica de la figura es cuatro.
\(\circ\) Exercise \(100\)
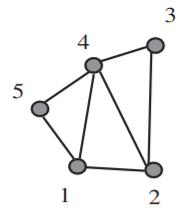
En la gráfica de la izquierda en la Figura 2.3.1, ¿cuál es el grado de cada vértice?
\(\circ\) Exercise \(101\)
Para cada gráfica de la Figura 2.3.1 ¿el número de vértices de grado impar es par o impar?
\(\rightarrow \; \cdot\) Exercise \(102\)
La suma de los grados de los vértices de una gráfica (finita) se relaciona de manera natural con el número de aristas.
- ¿Cuál es la relación? (Pista).
- Encuentra una prueba de que lo que dices es correcto que usa inducción en el número de aristas. (Pista).
- Encuentra una prueba de que lo que dices es correcto que usa inducción en el número de vértices.
- Encuentra una prueba de que lo que dices es correcto que no usa inducción. (Pista).
\(\cdot\) Exercise \(103\)
¿Qué se puede decir sobre el número de vértices de grado impar en una gráfica? (Pista).
2.3.2: Paseos y Senderos en Gráficas
Un paseo en una gráfica es una secuencia alterna\(v_{0}e_{1}v_{1} . . . e_{i}v_{i}\) de vértices y aristas de tal manera que el borde\(e_{i}\) conecta vértices\(v_{i−1}\) y\(v_{i}\). Una gráfica se llama conectada si, para cualquier par de vértices, hay una caminata que comienza en uno y termina en el otro.
Ejercicio\(104\)
¿Cuál de las gráficas de la Figura 2.3.1 está conectada?
\(\circ\) Exercise \(105\)
Un camino en una gráfica es un paseo sin vértices repetidos. Encuentra el camino más largo que puedas en la tercera gráfica de la Figura 2.3.1.
\(\circ\) Exercise \(106\)
Un ciclo en una gráfica es un paseo (con al menos un borde) cuyo primer y último vértice son iguales pero que no tiene otros vértices o aristas repetidos. ¿Qué gráficas de la Figura 2.3.1 tienen ciclos? ¿Cuál es el mayor número de aristas en un ciclo en la segunda gráfica de la Figura 2.3.1? ¿Cuál es el menor número de aristas en un ciclo en la tercera gráfica de la Figura 2.3.1?
\(\circ\) Exercise \(107\)
Un gráfico conectado sin ciclos se llama árbol. ¿Qué gráficas, en su caso, en la Figura 2.3.1 son árboles?
2.3.3: Recuento de vértices, aristas y caminos en árboles
\(\rightarrow \bullet\) Exercise \(108\)
Dibuja algunos árboles y sobre la base de tus ejemplos, haz una conjetura sobre la relación entre el número de vértices y aristas en un árbol. Demuestra tu conjetura. (Pista).
\(\cdot\) Exercise \(109\)
¿Cuál es el número mínimo de vértices de grado uno en un árbol finito? ¿Qué pasa si el número de vértices es mayor que uno? Demuestre que está en lo correcto. Consulta si puedes encontrar (y dar) más de una prueba. (Pista).
\(\rightarrow \; \cdot\) Exercise \(110\)
En un árbol en cualquier número de vértices, dados dos vértices, ¿cuántos caminos puedes encontrar entre ellos? Demuestre que está en lo correcto.
\(\rightarrow\;*\) Exercise \(111\)
¿Cuántos árboles hay en el conjunto de vértices\(\{1, 2\}\)? ¿En el set de vértices\(\{1, 2, 3\}\)? Cuando etiquetamos los vértices de nuestro árbol, consideramos el árbol que tiene bordes entre vértices\(1\) y\(2\) y entre vértices\(2\) y\(3\) diferente del árbol que tiene bordes entre vértices\(1\) y\(3\) y entre\(2\) y\(3\). Ver Figura 2.3.2.

¿Cuántos árboles (etiquetados) hay en cuatro vértices? ¿Cuántos árboles (etiquetados) hay con cinco vértices? No tienes muchos datos para adivinar, pero trata de adivinar una fórmula para el número de árboles etiquetados con vértices establecidos\(\{1, 2, · · · , n\}\). (Pista).
Ahora vamos a introducir un método para probar la fórmula que adivinaste. Dado un árbol con dos o más vértices, etiquetado con enteros positivos, definimos una secuencia\(b_{1}, b_{2}, . . .\) de enteros inductivamente de la siguiente manera: Si el árbol tiene dos vértices, la secuencia consiste en una entrada, es decir, la etiqueta del vértice con la etiqueta más grande. De lo contrario, deja\(a_{1}\) ser el vértice de grado más bajo numerado\(1\) en el árbol. Dejar\(b_{1}\) ser la etiqueta del vértice único en el árbol adyacente a\(a_1\) y anotar\(b_{1}\). Por ejemplo, en la primera gráfica de la Figura 2.3.1,\(a_{1}\) es\(1\) y\(b_{1}\) es\(2\). Dado a1 a través\(a_{i−1}\), deja\(a_i\) ser el vértice de grado más bajo numerado\(1\) en el árbol que obtienes al eliminar a1 a través\(a_{i−1}\) y deja\(b_{i}\) ser el vértice único en este nuevo árbol adyacente a\(a_{i}\). Por ejemplo, en la primera gráfica de la Figura 2.3.1,\(a_{2} = 2\) y\(b_{2} = 3\). Entonces\(a_{3} = 5\) y\(b_{3} = 4\). Usamos\(b\) para representar la secuencia de\(b_{i}s\) obtenemos de esta manera. En el árbol (la primera gráfica) de la Figura 2.3.1, la secuencia\(b\) es\(2344378\). (Si no está familiarizado con la definición inductiva (recursiva), es posible que desee escribir algunos otros árboles etiquetados en ocho vértices y construir la secuencia de\(b_{i}s\).)
Ejercicio\(112\)
- ¿Cuánto tiempo será la secuencia de si\(b_{i}s\) se calcula a partir de un árbol con\(n\) vértices (etiquetado con\(1\) through\(n\))?
- ¿Qué puedes decir del último miembro de la secuencia de\(b_{i}s\)? (Pista).
- ¿Se puede decir por la secuencia de\(b_i\) s qué\(a_1\) es? (Pista).
- Encuentra una bijección entre árboles etiquetados y algo que puedas “contar” que te dirá cuántos árboles etiquetados hay en los vértices\(n\) etiquetados. (Pista).
La secuencia\(b_{1}, b_{2}, . . . , b_{n−2}\) en el Problema 112 se denomina codificación Prüfer o código Prüfer para el árbol. Así es el código Prüfer para el árbol de la Figura 2.3.1\(234437\). Observe que no incluimos el término\(b_{n−1}\) en el código de Prüfer porque sabemos que lo es\(n\). Hay un buen poco de información interesante codificada en el código de Prüfer para un árbol.
Ejercicio\(113\)
¿Qué puedes decir sobre los vértices de grado uno del código Prüfer para un árbol etiquetado con los enteros de\(1\) a\(n\)? (Pista).
Ejercicio\(114\)
¿Qué puedes decir del código Prüfer para un árbol con exactamente dos vértices de grado\(1\) (y quizás algunos vértices con otros grados también)? ¿Caracteriza esto a tales árboles?
\(\rightarrow\) Exercise \(115\)
¿Qué se puede determinar sobre el grado del vértice etiquetado\(i\) a partir del código Prüfer del árbol? (Pista).
\(\rightarrow\) Exercise \(116\)
¿Cuál es el número de árboles (etiquetados) en\(n\) vértices con tres vértices de grado\(1\)? (Supongamos que están etiquetados con los enteros\(1\) a través de\(n\).) Este problema volverá a aparecer en el siguiente capítulo después de algún material que lo facilitará. (Pista).
2.3.4: Árboles de expansión
Muchas de las aplicaciones de los árboles surgen al tratar de encontrar una manera eficiente de conectar todos los vértices de una gráfica. Por ejemplo, en una red telefónica, en un momento dado tenemos un cierto número de cables (o canales de microondas, o canales celulares) disponibles para su uso. Estos cables o canales van de un lugar específico a un lugar específico. Por lo tanto, los cables o canales pueden considerarse como bordes de una gráfica y los lugares en los que se conectan los cables pueden considerarse como vértices de esa gráfica. Un árbol cuyos bordes son algunos de los bordes de una gráfica\(G\) y cuyos vértices son todos los vértices de la gráfica\(G\) se denomina árbol de expansión de\(G\). Un árbol de expansión para una red telefónica nos dará una forma de enrutar llamadas entre dos vértices cualesquiera de la red. En la Figura 2.2.3 mostramos una gráfica y todos sus árboles de expansión.
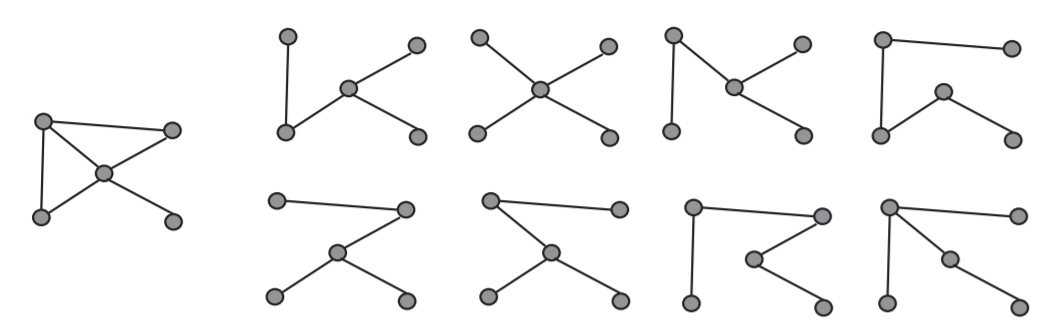
Ejercicio\(117\)
Demuestre que cada gráfica conectada tiene un árbol de expansión. Es posible encontrar una prueba que comience con la gráfica y trabaje “hacia abajo” hacia el árbol de expansión y encontrar una prueba que comience con solo los vértices y trabaje “arriba” hacia el árbol de expansión. ¿Puedes encontrar ambos tipos de comprobantes?
2.3.5: Árboles de expansión de costo mínimo
Nuestra motivación para hablar de árboles de expansión fue la idea de encontrar un número mínimo de bordes que necesitamos para conectar todos los bordes de una red de comunicación juntos. En muchos casos los bordes de una red de comunicación vienen con costos asociados con ellos. Por ejemplo, un operador de telefonía celular cobra otro cuando un cliente del primero usa una antena del otro. Supongamos que una empresa tiene oficinas en varias ciudades y quiere armar una red de comunicación que conecte sus diversas ubicaciones con comunicaciones informáticas de alta velocidad, pero hacerlo a un costo mínimo. Entonces quiere tomar una gráfica cuyos vértices son las ciudades en las que tiene oficinas y cuyos bordes representan posibles líneas de comunicación entre las ciudades. Por supuesto, no necesariamente habrá líneas entre cada par de ciudades, y la compañía no querrá pagar por una línea que conecte ciudad\(i\) y ciudad\(j\) si ya puede conectarlas indirectamente usando otras líneas que haya elegido. Por lo tanto, querrá elegir un árbol de expansión de costo mínimo entre todos los árboles de expansión de la gráfica de comunicaciones. Por razones de esta aplicación, si tenemos una gráfica con números asignados a sus bordes, la suma de los números en los bordes de un árbol de expansión de se\(G\) llamará el costo del árbol de expansión.
\(\rightarrow\) Exercise \(118\)
Describir un método (o mejor, dos métodos diferentes en al menos un aspecto) para encontrar un árbol de expansión de costo mínimo en una gráfica cuyos bordes están etiquetados con costos, siendo el costo en una arista el costo de incluir ese borde en un árbol de expansión. Demuestra que tu (s) método (s) funciona (n (Pista).
El método que utilizó en el Problema 118 se llama método codicioso, porque cada vez que elige una arista, elige la arista menos costosa disponible para usted.
2.3.6: La recurrencia de deleción/contracción para árboles de expansión
Hay dos operaciones en gráficas que podemos aplicar para obtener una recurrencia (aunque de tipo más general que las que hemos estudiado para secuencias) que nos permitirán calcular el número de árboles de expansión de una gráfica. Cada una de las operaciones se aplica a un borde\(e\) de una gráfica\(G\). El primero se llama eliminación; eliminamos el borde\(e\) de la gráfica eliminándolo del conjunto de bordes. La Figura 2.3.4 muestra cómo podemos eliminar bordes de una gráfica para obtener un árbol de expansión.
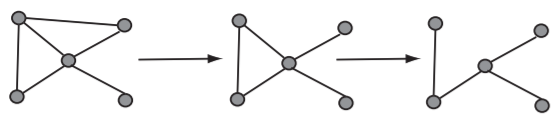
La segunda operación se llama contracción.
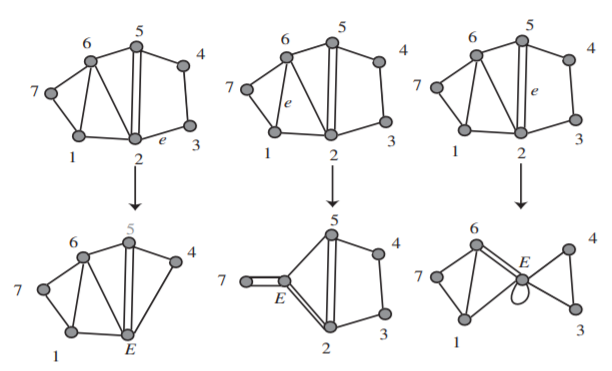
Las contracciones de tres bordes diferentes en la misma gráfica se muestran en la Figura 2.3.5. Intuitivamente, contraemos una arista encogiéndola en longitud hasta que sus puntos finales coincidan; dejamos que el resto de la gráfica “vaya por el paseo”. Para ser más precisos, contratamos el borde\(e\) con puntos finales\(v\) y de la\(w\) siguiente manera:
- eliminar todas las aristas que tengan uno\(v\)\(w\) o ambos como punto final del conjunto de aristas,
- eliminar\(v\) y\(w\) del conjunto de vértices,
- añadir un nuevo vértice\(E\) al conjunto de vértices,
- agregue una arista de\(E\) a cada vértice restante que solía ser un punto final de una arista cuyo otro punto final era\(v\) o\(w\), y agregue una arista de\(E\) a\(E\) para cualquier arista que no sea e cuyos extremos estuvieran en el conjunto\(\{v,w\}\).
Usamos\(G − e\) (leemos como\(G\) menos\(e\)) para representar el resultado de eliminar\(e\) de\(G\), y usamos\(G/e\) (leer como\(G\) contrato\(e\)) para representar el resultado de la contratación\(e\) de\(G\).
\(\rightarrow \; \cdot\) Exercise \(119\)
- ¿Cómo se relacionan el número de árboles de expansión de\(G\) no contener el borde\(e\) y el número de árboles de expansión de\(G\) contener e con el número de árboles de expansión de\(G − e\) y\(G/e\)? (Pista).
- Se usa\(\#(G)\) para representar el número de árboles que abarcan\(G\) (de modo que, por ejemplo,\(\#(G/e)\) representa el número de árboles que abarcan de\(G/e\)). Encuentra una expresión para # (\(G\)) en términos de\(\#(G/e)\) y\(\#(G − e)\). Esta expresión se llama la recurrencia deleción-contracción.
- Utilice la recurrencia de la parte anterior para calcular el número de árboles de expansión de la gráfica en la Figura 2.3.6
2.3.7: Trayectorias más cortas en gráficas
Supongamos que una empresa tiene una oficina principal en una ciudad y oficinas regionales en otras ciudades. La mayor parte de la comunicación en la empresa es entre la oficina principal y las oficinas regionales, por lo que la empresa quiere encontrar un árbol de expansión que minimice no el costo total de todos los bordes, sino más bien el costo de comunicación entre la oficina principal y cada una de las oficinas regionales. No está claro que tal árbol de expansión siquiera exista. Este problema es un caso especial de los siguientes. Tenemos una gráfica conectada con números no negativos asignados a sus bordes. (En esta situación a estos números se les suele llamar pesos). La longitud (ponderada) de una ruta en la gráfica es la suma de los pesos de sus bordes. La distancia entre dos vértices es la longitud menor (ponderada) de cualquier trayectoria entre los dos vértices. Dado un vértice\(v\), nos gustaría saber la distancia entre\(v\) y cada vértice, y nos gustaría saber si hay un árbol de expansión de\(G\) tal manera que la longitud del camino en el árbol de expansión desde\(v\) hasta cada vértice\(x\) sea la distancia de\(v\) a \(x\)pulg\(G\).
Ejercicio\(120\)
Demostrar que el siguiente algoritmo (conocido como algoritmo de Dijkstra) aplicado a una gráfica ponderada cuyos vértices están etiquetados\(1\)\(n\) para dar, para cada uno\(i\), la distancia de vértice\(1\) a\(i\) as\(d(i)\).
- Vamos\(d(1) = 0\). Dejemos\(d(i) = 1\) para todos los demás\(i\). Vamos\(v(1)=1\). Dejemos\(v(j) = 0\) para todos los demás\(j\). Para cada uno\(i\) y\(j\), deje\(w(i, j)\) ser el peso mínimo de un borde entre\(i\) y\(j\), o\(1\) si no existen tales bordes. Vamos\(k = 1\). Vamos\(t = 1\).
- Para cada uno\(i\), si se\(d(i) > d(k) + w(k, i)\) deja\(d(i) = d(k) + w(k, i)\).
- Entre los que tienen\(i\)\(v(i) = 0\), elige uno con\(d(i)\) un mínimo, y deja\(k = i\). Incrementar\(t\) en 1. Vamos\(v(i) = 1\).
- Repita los dos pasos anteriores hasta\(t = n\).
Ejercicio\(121\)
¿Hay un árbol de expansión tal que la distancia de vértice\(1\) a vértice\(i\) dada por el algoritmo en Problema 120 es la distancia de vértice\(1\) a vértice\(i\) en el árbol (usando los mismos pesos en los bordes, por supuesto)?


