2.4: Aplicaciones de la Inducción y Recursión en Combinatoria y Teoría de Gráficas (Ejercicios)

1. Utilice la definición inductiva de an para probarlo\((ab)^{n} = a^{n}b^{n}\) para todos los enteros no negativos\(n\).

2. Dar una definición inductiva\(\bigcup\limits_{i=1}^{n}S_{i}\) y utilizarla y los dos establecen ley distributiva para probar la ley distributiva\(A \cap \bigcup\limits_{i=1}^{n}S_{i} = \bigcup\limits_{i=1}^{n} A \cap S_{i}\).

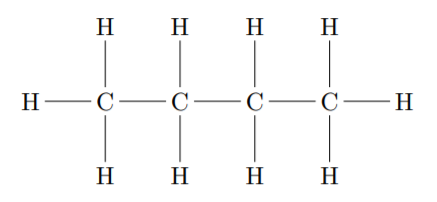
\(\rightarrow\)3. Una molécula de hidrocarburo es una molécula cuyos únicos átomos son átomos
de carbono o átomos de hidrógeno. En un modelo molecular simple de un hidrocarburo, un átomo de carbono se unirá exactamente a otros cuatro átomos y el átomo de hidrógeno se unirá exactamente a otro átomo. Dicho modelo se muestra en la Figura 2.4.1. Representamos un compuesto hidrocarbonado con una gráfica cuyos vértices están etiquetados con\(C\)'s y\(H\)'s de manera que cada\(C\) vértice tiene grado cuatro y cada\(H\) vértice tiene grado uno. Un hidrocarburo se llama “alcano” si la gráfica es un árbol. Ejemplos comunes son metano (gas natural), butano (una versión del cual se muestra en la Figura 2.4.1), propano, hexano (gasolina ordinaria), octano (para hacer que la gasolina arda más lentamente), etc.

1. ¿Cuántos vértices están etiquetados\(H\) en la gráfica de un alcano con exactamente\(n\) vértices etiquetados\(C\)?
2. Un alcano se llama butano si tiene cuatro átomos de carbono. ¿Por qué decimos que una versión de butano se muestra en la Figura 2.4.1?

Figura\(\PageIndex{1}\): Un modelo de una molécula de butano. (Copyright; autor vía fuente)

4.

1. Dar una recurrencia por el número de formas de dividir a\(2n\) las personas en conjuntos de dos para los juegos de tenis. (No te preocupes por quién sirve primero.)
2. Dar una recurrencia por el número de formas de dividir a\(2n\) las personas en conjuntos de dos para los juegos de tenis y determinar quién sirve primero.)

\(\rightarrow\)5. Dar una recurrencia por el número de formas de dividir a\(4n\) las personas en conjuntos de cuatro para los juegos de bridge. (No te preocupes por cómo se sientan alrededor de la mesa del puente o quién es el primer distribuidor).

6. Usa la inducción para probar tu resultado en el Problema Suplementario 2 al final del Capítulo 1.

7. Dar una definición inductiva de la notación del producto\(\prod\limits^{n}_{i=1}a_{i}\).

8. Usando el hecho de que\((ab)^{k} = a^{k}b^{k}\), usa tu definición inductiva de notación de
producto en el Problema 7 para probarlo\(\left(\prod\limits^{n}_{i=1}a_{i}\right)^{k} = \prod\limits^{n}_{i=1}a_{i}^{k}\).

\(\rightarrow\)9. ¿Cuántos árboles etiquetados en\(n\) vértices tienen exactamente cuatro vértices de grado\(1\)? (Este problema también aparece en el siguiente capítulo ya que algunas ideas en ese capítulo lo hacen más sencillo).

\(\rightarrow *\)10. La secuencia de grados de una gráfica es una lista de los grados de los vértices en orden no creciente. Por ejemplo, la secuencia de grados de la primera gráfica en la Figura 2.3.3 es\((4, 3, 2, 2, 1)\). Para una gráfica con vértices etiquetados\(1\) a través\(n\), la secuencia ordenada de grados de la gráfica es la secuencia\(d_1, d_2, . . . d_n\) en la que\(d_{i}\) se encuentra el grado de vértice\(i\). Por ejemplo, la secuencia ordenada de grados de la primera gráfica en la Figura 2.3.1 es\((1, 2, 3, 3, 1, 1, 2, 1)\).

1. ¿Cuántos árboles etiquetados hay en los\(n\) vértices con secuencia ordenada de grados\(d_{1}, d_{2}, . . . d_{n}\)? (Este problema vuelve a aparecer en el siguiente capítulo ya que algunas ideas de ese capítulo lo hacen más sencillo).
2. ¿Cuántos árboles etiquetados hay en los\(n\) vértices con la secuencia de grados en la que\(d\) aparece el grado\(i_d\) veces?