7.2: Propiedades de las funciones

Última actualización
Guardar como PDF

Page ID: 117282

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Propiedades

Considere las siguientes funciones:

Dejar$A = \{1, 2, 3, 4\}$$B = \{a, b, c, d\}\text{,}$ y definir$f:A \rightarrow B$ por

\ begin {ecuación*} f (1) = a, f (2) = b, f (3) = c\ textrm {y} f (4) = d\ end {ecuación*}

Dejar$A = \{1, 2, 3, 4\}$$B = \{a, b, c, d\}\text{,}$ y definir$g:A \rightarrow B$ por

\ comenzar {ecuación*} g (1) = a, g (2) = b, g (3) = a\ textrm {y} g (4) = b.\ final {ecuación*}

La primera función, nos$f\text{,}$ da más información sobre el conjunto$B$ que la segunda función,$g\text{.}$ ya que$A$ claramente tiene cuatro elementos, nos$f$ dice que$B$ contiene al menos cuatro elementos ya que cada elemento de$A$ está mapeado sobre un elemento diferente de $B\text{.}$Las propiedades que$f$ tiene, y$g$ no tiene, son las propiedades más básicas que buscamos en una función. Las siguientes definiciones resumen el vocabulario básico para las propiedades de las funciones.

Definición$\PageIndex{1}$: Injective Function, Injection

Una función$f: A \rightarrow B$ es inyectable si

\ comenzar {ecuación*}\ para todos a, b\ en A, a\ neq b\ fila derecha f (a)\ neq f (b)\ fin {ecuación*}

Una función inyectable se llama inyección, o función uno a uno.

Observe que la condición para una función de inyección es lógicamente equivalente a

\ begin {ecuación*} f (a) = f (b)\ Fila derecha a = b\ texto {.} \ end {ecuación*}

para todos$a, b\in A\text{.}$ Esta suele ser una condición más conveniente de probar que lo que se da en la definición.

Definición$\PageIndex{2}$: Surjective Function, Surjection

Una función$f: A \rightarrow B$ es suryectiva si su rango,$f(A)\text{,}$ es igual a su codominio,$B\text{.}$ Una función suryectiva se llama una suryección, o una función onto.

Observe que la condición para una función suryectiva es equivalente a

\ begin {ecuación*}\ textrm {Para todos} b\ en B\ textrm {, existe} a\ en A\ textrm {tal que} f (a) =b\ text {.} \ end {ecuación*}

Definición$\PageIndex{3}$: Bijective Function, Bijection

Una función$f: A \rightarrow B$ es biyectiva si es tanto inyectiva como suryectiva. Las funciones biyectivas también se llaman uno-a-uno, en funciones.

La función con la$f$ que abrimos esta sección es biyectiva. La función no$g$ es ni inyectable ni suryectiva.

Ejemplo$\PageIndex{1}$: Injective but Not Surjective Function

Dejar$A = \{1, 2, 3\}$$B = \{a, b, c, d\}\text{,}$ y definir$f:A \rightarrow B$ por$f(1) = b\text{,}$$f(2) = c\text{,}$ y$f(3) = a\text{.}$ Entonces$f $ es inyectable pero no suryectiva.

Ejemplo$\PageIndex{2}$: Characteristic Functions

La función característica,$\chi _S\text{,}$ en el Ejercicio 7.1.4 es suryectiva si$S$ es un subconjunto propio de$A\text{,}$ pero nunca inyectable si$\lvert A \rvert \gt 2\text{.}$

Contando

Ejemplo$\PageIndex{3}$: Seating Students

$A$Sea el conjunto de alumnos que están sentados en un aula, que$B$ sea el conjunto de asientos en el aula, y que$s$ sea la función que mapee a cada alumno en la silla en la que está sentado. ¿Cuándo es$s$ uno a uno? ¿Cuándo está en? En circunstancias normales, siempre$s$ sería inyectable ya que no habría dos estudiantes diferentes en la misma silla. $s$Para que sea suryectiva, necesitamos que se utilicen todas las butacas, así$s$ es una sobrejección si el aula está llena al aforo.

Las funciones también se pueden utilizar para contar los elementos en conjuntos finitos grandes o en conjuntos infinitos. Digamos que quisimos contar a los ocupantes en un auditorio que contiene mil 500 asientos. Si cada asiento está ocupado, la respuesta es obvia, mil 500 personas. Lo que hemos hecho es establecer una correspondencia uno a uno, o bijección, de asientos a personas. Formalizamos en una definición.

Definición $\PageIndex{4}$: Cardinality

Se dice que dos conjuntos tienen la misma cardinalidad si existe una biyección entre ellos. Si un conjunto tiene la misma cardinalidad que el conjunto$\{1,2,3,\ldots , n\}\text{,}$ entonces decimos que su cardinalidad es$n\text{.}$

La función$f$ que abrió esta sección sirve para mostrar que los dos conjuntos$A=\{1, 2, 3, 4\}$ y$B=\{a, b, c, d\}$ tienen la misma cardinalidad. Observe al aplicar la definición de cardinalidad, en realidad no parecemos contar ninguno de los dos conjuntos, solo coincidimos con los elementos. Sin embargo, hacer coincidir las letras$B$ con los números 1, 2, 3 y 4 es precisamente como contamos las letras.

Definición$\PageIndex{5}$: Countable Set

Si un conjunto es finito o tiene la misma cardinalidad que el conjunto de enteros positivos, se denomina conjunto contable.

Ejemplo$\PageIndex{4}$: Counting the Alphabet

El alfabeto$\{A, B, C, . . . , Z\}$ tiene cardinalidad 26 a través de la siguiente biyección en el conjunto$\{1,2,3,\ldots ,26\}\text{.}$

\ begin {ecuación*}\ begin {array} {ccccc} A & B & C &\ cdots &\ cdots & Z\\ downarrow &\ downarrow &\ downarrow &\ cdots &\ downarrow\\ 1 & 2 & 3 &\ cdots & 26\\ end {array}\ text {.} \ end {ecuación*}

Ejemplo$\PageIndex{5}$: As Many Evens as All Positive Integers

Recordemos que$2\mathbb{P}= \{b\in \mathbb{P} \mid b= 2k \textrm{ for some } k \in \mathbb{P} \}\text{.}$ Paradójicamente,$2\mathbb{P}$ tiene la misma cardinalidad que el conjunto$\mathbb{P}$ de enteros positivos. Para probar esto, debemos encontrar una bijección de$\mathbb{P}$ a$2\mathbb{P}\text{.}$ Tal función no es única, pero esta es la más simple:$f:\mathbb{P} \rightarrow 2\mathbb{P}$ donde$f(m) = 2m\text{.}$ Dos afirmaciones deben probarse para justificar nuestra afirmación que$f$ es una bijección:

$f$es uno a uno.
Prueba: Dejemos$a, b \in \mathbb{P}$ y supongamos que$f(a) = f(b)\text{.}$ debemos probar que$a = b\text{.}$
\ comenzar {ecuación*} f (a) = f (b)\ Longrightarrow 2a = 2b\ Longrightarrow a = b.\ end {ecuación*}
$f $está en.
Prueba: Vamos$b \in 2\mathbb{P}\text{.}$ Queremos mostrar que existe un elemento$a \in \mathbb{P}$ tal que$f(a) = b\text{.}$ si$b \in 2\mathbb{P}\text{,}$$b = 2k$ para algunos$k \in \mathbb{P}$ por la definición de$2\mathbb{P}\text{.}$ Así tenemos$f(k) = 2k = b\text{.}$ De ahí que cada elemento de 2$\mathbb{P}$ es la imagen de algún elemento de$\mathbb{P}\text{.}$

Otra forma de ver cualquier función con$\mathbb{P}$ como su dominio es crear una lista del formulario$f(1),f(2), f(3), \ldots\text{.}$ En el ejemplo anterior, la lista es$2, 4, 6, \ldots\text{.}$ Esta lista infinita claramente no tiene entradas duplicadas y cada entero par positivo aparece en la lista eventualmente.

Una función$f:\mathbb{P}\to A$ es una bijección si la lista infinita no$f(1), f(2), f(3), \ldots$ contiene duplicados, y cada elemento de$A$ aparece en la lista. En este caso, decimos que el$A$ es contablemente infinito, o simplemente contable.

Los lectores que han estudiado análisis reales deben recordar que el conjunto de números racionales es un conjunto contable, mientras que el conjunto de números reales no es un conjunto contable. Consulte los ejercicios al final de esta sección para ver otro ejemplo de tal conjunto.

Cerramos esta sección con un teorema llamado Principio de Pigeonhole, que tiene numerosas aplicaciones a pesar de que es una afirmación obvia, de sentido común. Nunca subestimes la importancia de las ideas simples. El Principio Paloma establece que si hay más palomas que palomas, entonces dos o más palomas deben compartir el mismo palomillo. Sigue una declaración matemática más rigurosa del principio.

Teorema$\PageIndex{1}$: The Pigeonhole Principle

Dejar$f$ ser una función de un conjunto finito$X$ a un conjunto finito$Y\text{.}$ Si$n\geq 1$ y$\lvert X\rvert > n\lvert Y\rvert\text{,}$ entonces existe un elemento de$Y$ eso es la imagen bajo$f$ de al menos$n + 1$ elementos de X.

Prueba

Supongamos que no existe tal elemento. Para cada$y \in Y\text{,}$ let$A_y = \{x\in X \mid f(x) =y \}\text{.}$ Entonces debe ser que$\lvert A_y \rvert \leq n\text{.}$ Además, el conjunto de no vacíos$A_y$ forman una partición de$X\text{.}$ Por lo tanto,

\ begin {ecuación*}\ lvert X\ rvert =\ suma_ {y\ in Y} {\ lvert a_Y\ rvert}\ leq n\ lvert Y\ rvert\ rvert\ end {ecuación*}

lo cual es una contradicción.

Ejemplo$\PageIndex{6}$: A Duplicate Name is Assured

Supongamos que una habitación contiene cuatro estudiantes con los nombres de pila John, James y Mary. Demostrar que dos alumnos tienen el mismo nombre de pila. Podemos visualizar un mapeo desde el conjunto de alumnos hasta el conjunto de nombres; cada alumno tiene un nombre. El principio del casillero se aplica con$n = 1\text{,}$ y podemos concluir que al menos dos de los alumnos tienen el mismo nombre.

Ejercicios

Ejercicio$\PageIndex{1}$

Determinar cuáles de las funciones en el Ejercicio 7.1.1 de la Sección 7.1 son uno a uno y cuáles están en.

Responder: La única función uno a uno y la única función on es$f\text{.}$

Ejercicio$\PageIndex{2}$

Determine todas las biyecciones desde$\{1, 2, 3\}$$\{a, b, c\}\text{.}$
Determine todas las biyecciones desde$\{1, 2, 3\}$$\{a, b, c, d\}\text{.}$

Ejercicio$\PageIndex{3}$

¿Cuáles de los siguientes son uno a uno, a, o ambos?

$f_1:\mathbb{R} \rightarrow \mathbb{R}$definido por$f_1(x) = x^3 - x\text{.}$
$f_2 :\mathbb{Z} \rightarrow \mathbb{Z}$definido por$f_2(x)= -x + 2\text{.}$
$f_3:\mathbb{N} \times \mathbb{N}\to \mathbb{N}$definido por$f_3(j, k) =2^j3^k\text{.}$
$f_4 :\mathbb{P} \rightarrow \mathbb{P}$definido por$f_4(n)=\lceil n/2\rceil\text{,}$ donde$\lceil x\rceil$ es el techo$x\text{,}$ del entero más pequeño mayor que o igual a$x\text{.}$
$f_5 :\mathbb{N} \rightarrow \mathbb{N}$definido por$f_5(n)=n^2+n\text{.}$
$f_6:\mathbb{N} \rightarrow \mathbb{N} \times \mathbb{N}$definido por$f_6(n)= (2n, 2n+1)\text{.}$

Responder

$f_1$está en pero no uno a uno:$f_1(0)=f_1(1)\text{.}$
$f_2$es uno a uno y en.
$f_3$es uno a uno pero no a.
$f_4$está sobre pero no uno a uno.
$f_5$es uno a uno pero no a.
$f_6$es uno a uno pero no a.

Ejercicio$\PageIndex{4}$

¿Cuáles de las siguientes son inyecciones, sobreyecciones o biyecciones en$\mathbb{R}\text{,}$ el conjunto de números reales?

$f(x) = -2x\text{.}$
$g(x) = x^2- 1\text{.}$
$\displaystyle h(x)=\left\{ \begin{array}{cc} x & x < 0 \\ x^2 & x\geq 0 \\ \end{array} \right.$
$\displaystyle q(x)=2^x$
$\displaystyle r(x) =x^3$
$\displaystyle s(x) = x^3-x$

Ejercicio$\PageIndex{5}$

Supongamos que$m$ pares de calcetines están mezclados en el cajón de tus calcetines. Usa el Principio de Pigeonhole para explicar por qué, si eliges$m + 1$ calcetines al azar, al menos dos formarán un par a juego.

Responder: Dejar$X=\{\textrm{socks selected}\}$$Y=\{\textrm{pairs of socks}\}$ y definir$f:X \to Y$ dónde está$f(x) =$ el par de calcetines$x$ al que pertenece. Por el principio Pigeonhole, existen dos calcetines que fueron seleccionados del mismo par.

Ejercicio$\PageIndex{6}$

En sus propias palabras explica la afirmación “Los conjuntos de enteros e incluso enteros tienen la misma cardinalidad”.

Ejercicio$\PageIndex{7}$

Let$A =\text{ }\{1, 2, 3, 4, 5\}\text{.}$ Find funciones, si existen que tienen las propiedades especificadas a continuación.

Una función que es uno a uno y sobre.
Una función que no es ni uno a uno ni on.
Una función que es uno a uno pero no sobre.
Una función que está sobre pero no uno a uno.

Responder

$f(n)=n\text{,}$por ejemplo
$f(n)=1\text{,}$por ejemplo
Ninguno existe.
Ninguno existe.

Ejercicio$\PageIndex{8}$

Definir funciones, si existen, sobre los enteros positivos,$\mathbb{P}\text{,}$ con las mismas propiedades que en Ejercicio$\PageIndex{7}$ (si es posible).
Dejar$A$ y$B$ ser conjuntos finitos donde ¿$|A|=|B|\text{.}$Es posible definir una función$f:A \rightarrow B$ que sea uno a uno pero no sobre? ¿Es posible encontrar una función$g:A \rightarrow B$ que esté sobre pero no uno a uno?

Ejercicio$\PageIndex{9}$

Demostrar que el conjunto de números naturales es contable.
Demostrar que el conjunto de enteros es contable.
Demostrar que el conjunto de números racionales es contable.

Responder

Uso$s:\mathbb{N}\to \mathbb{P}$ definido por$s(x)=x+1\text{.}$
Utilice la función$f:\mathbb{N}\to \mathbb{Z}$ definida por$f(\text{x0}=x/2$ if$x$ es par y$f(x)=-(x+1)/2$ if$x$ es impar.
La prueba se debe a Georg Cantor (1845-1918), e implica enumerar los racionales a través de un procedimiento definido para que no se omita ninguno y se eviten duplicaciones. En la primera fila listan todos los racionales no negativos con denominador 1, en la segunda todos los racionales no negativos con denominador 2, etc. En este listado, por supuesto, hay duplicaciones, por ejemplo,$0/1=0/2=0\text{,}$$1/1=3/3=1\text{,}$$6/4=9/6=3/2\text{,}$ etc. Para obtener una lista sin duplicaciones siga las flechas de la Figura $\PageIndex{1}$, enumerando solo los números con un círculo.
Obtenemos:$0,1,1/2,2,3,1/3,1/4,2/3,3/2,4/1,\ldots$ Cada racional no negativo aparece en esta lista exactamente una vez. Ahora debemos insertar en esta lista los racionales negativos, y seguir el mismo esquema para obtener:
\ begin {equation*} 0,1, -1,1/2, -1/2,2, -2,3, -3,1/3, -1/3,\ ldots\ end {equation*} los
cuales se pueden emparejar con los elementos de$\mathbb{N}\text{.}$

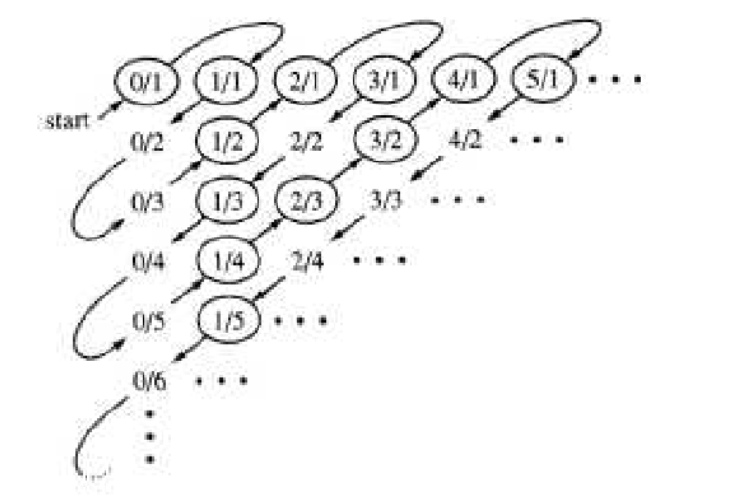
$clipboard_ef24965abd4b36efa668a99d42285c7d8.png$

Figura$\PageIndex{1}$: Enumeración de los números racionales.

Ejercicio$\PageIndex{10}$

Demostrar que el conjunto de cadenas finitas de 0 y 1 es contable.
Demostrar que el conjunto de enteros impares es contable.
Demostrar que el conjunto$\mathbb{N}\times \mathbb{N}$ es contable.

Ejercicio$\PageIndex{11}$

Usa el Principio de Agujero Paloma para probar que una inyección no puede existir entre un conjunto finito$A$ y un conjunto finito$B$ si la cardinalidad de$A$ es mayor que la cardinalidad de$B\text{.}$

Responder: Let$f$ be any function from$A$ into$B\text{.}$ By the Pigeonhole principle with$n=1\text{,}$ there exist a element of$B$ that is the image of at least two elements of$A\text{.}$ Therefore, no$f$ es una inyección.

Ejercicio$\PageIndex{12}$

Las propiedades importantes de las relaciones generalmente no son de interés para las funciones. La mayoría de las funciones no son reflexivas, simétricas, antisimétricas o transitivas. ¿Se pueden dar ejemplos de funciones que sí tienen estas propiedades?

Ejercicio$\PageIndex{13}$

Demostrar que el conjunto de todas las secuencias infinitas de 0 y 1 no es un conjunto contable.

Responder

La prueba es indirecta y sigue una técnica llamada proceso diagonal Cantor. Supongamos al contrario que el conjunto es contable, entonces los elementos pueden ser listados:$n_1,n_2,n_3,\ldots$ donde cada uno$n_i$ es una secuencia infinita de 0s y 1s. Considere la matriz:

\ begin {ecuación*}\ begin {array} {c} n_1=n_ {11} n_ {12} n_ {13}\ cdots\\ n_2=n_ {21} n_ {22} n_ {23}\ cdots\\ n_3=n_ {31} n_ {32} n_ {33}\ cdots\\ cuádruple\ vdots\\\ end {array}\ end {ecuación*}

Suponemos que esta matriz contiene todas las secuencias infinitas de 0s y 1s. Considere la secuencia$s$ definida por$s_i=\begin{cases} 0 & \textrm{ if } n_{\textrm{ii}}=1 \\ 1 & \textrm{ if } n_{\textrm{ii}}=0 \end{cases}$

Observe que$s$ difiere de cada uno$n_i$ en la posición$i$ th y así no puede estar en la lista. Esto es una contradicción, que completa nuestra prueba.

Ejercicio$\PageIndex{14}$

Demostrar que el conjunto de todas las funciones en los enteros es un conjunto incontable.

Ejercicio$\PageIndex{15}$

Dados cinco puntos en la plaza unitaria,$\{(x,y) \mid 0 \leq x, y \leq 1 \}\text{,}$ demostrar que hay dos de los puntos a una distancia de no más que uno$\frac{\sqrt{2}}{2}$ del otro.

Search

Text Color

Text Size

Margin Size

Font Type