11.2: Sistemas algebraicos

Última actualización
Guardar como PDF

Page ID: 117350

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Un sistema algebraico es un sistema matemático que consiste en un conjunto llamado dominio y una o más operaciones en el dominio. Si$V$ es el dominio y$*_1, *_2, \ldots , *_n$ son las operaciones,$\left[V;*_1, *_2, \ldots , *_n\right]$ denota el sistema matemático. Si el contexto es claro, esta notación se abrevía como$V\text{.}$

Monoides en Dos Niveles

Considera los siguientes dos ejemplos de sistemas algebraicos.

$B^*$Sea el conjunto de todas las cadenas finitas de 0's y 1's incluyendo la cadena nula (o vacía), Se obtiene$\lambda\text{.}$ un sistema algebraico agregando la operación de concatenación. La concatenación de dos cadenas es simplemente el enlace de las dos cadenas juntas en el orden indicado. La concatenación de cadenas$a$ con$b$ se denota$a+b\text{.}$ Por ejemplo,$01101+101 =01101101$ y$\lambda +100 = 100\text{.}$ Tenga en cuenta que la concatenación es una operación asociativa y esa$\lambda$ es la identidad para la concatenación.
Una nota sobre la notación: No hay un símbolo estándar para la concatenación. Hemos optado por$+$ ser consistentes con la notación utilizada en Python y Sage para la concatenación.
Dejar$M$ ser cualquier conjunto no vacío y dejar que * sea cualquier operación en$M$ que sea asociativa y tenga una identidad en$M\text{.}$ Cualquier sistema de este tipo se llama monoide. Presentamos los monoides brevemente aquí, pero los discutiremos más a fondo en el Capítulo 14

Nuestro segundo ejemplo puede parecer extraño, pero lo incluimos para ilustrar un punto. El sistema algebraico$\left[B^*;+\right]$ es un caso especial de$[M;*]\text{.}$ La mayoría de nosotros estamos mucho más cómodos con$B^*$ que con$M\text{.}$ Sin duda, la razón es que los elementos en$B^*$ son más concretos. Sabemos cómo se ven y exactamente cómo se combinan. La descripción de$M$ es tan vaga que ni siquiera sabemos cuáles son los elementos, mucho menos cómo se combinan. Por qué alguien querría estudiar$M\text{?}$ La razón está relacionada con esta pregunta: ¿Qué teoremas son de interés en un sistema algebraico? Responder a esta pregunta es uno de nuestros principales objetivos en este capítulo. Ciertas propiedades de los sistemas algebraicos se denominan propiedades algebraicas, y cualquier teorema que diga algo sobre las propiedades algebraicas de un sistema sería de interés. La capacidad de identificar lo que es algebraico y lo que no lo es es una de las habilidades que debes aprender de este capítulo.

Ahora, volvamos a la pregunta de por qué estudiamos$M\text{.}$ Nuestra respuesta es ilustrar la utilidad de$M$ con un teorema sobre$M\text{.}$

Teorema$\PageIndex{1}$: A Monoid Theorem

Si$a\text{,}$$b$ son elementos de$M$ y$a * b = b * a\text{,}$ luego$(a * b) * (a * b) = (a * a) * (b * b)\text{.}$

Prueba: \ begin {ecuación*}\ begin {split} (a*b) * (a*b) &=a* (b* (a*b))\ quad\ textrm {¿Por qué?} \\ &=a* ((b*a) *b)\ quad\ textrm {¿Por qué?} \\ &= a* ((a*b) *b)\ quad\ textrm {¿Por qué?} \\ &= a* (a* (b*b))\ quad\ textrm {¿Por qué?} \\ &= (a*a) * (b*b)\ quad\ textrm {¿Por qué?} \ end {split}\ end {ecuación*}

El poder de este teorema es que se puede aplicar a cualquier sistema algebraico que$M$ describa. Dado que$B^*$ es uno de esos sistemas, podemos aplicar Teorema$\PageIndex{1}$ a cualquiera de las dos cadenas que conmuten. Por ejemplo, 01 y 0101. Aunque podría haberse probado un caso especial de este teorema$B^*\text{,}$ ya que no habría sido más fácil de probar, y no nos habría dado ninguna idea de otros casos especiales de$M\text{.}$

Ejemplo$\PageIndex{1}$: Another Monoid

Considerar el conjunto de matrices$2\times 2$ reales,$M_{2\times 2}(\mathbb{R})\text{,}$ con la operación de multiplicación matricial. En este contexto, el Teorema$\PageIndex{1}$ puede interpretarse como diciendo que si$A B = B A\text{,}$ entonces$(A B)^2= A^2B^2\text{.}$ Un par de matrices a las que se aplica este teorema es$\left( \begin{array}{cc} 2 & 1 \\ 1 & 2 \\ \end{array} \right)$ y$\left( \begin{array}{cc} 3 & -4 \\ -4 & 3 \\ \end{array} \right)\text{.}$

Niveles de Abstracción

Una de las herramientas fundamentales en matemáticas es la abstracción. Hay tres niveles de abstracción que identificaremos para los sistemas algebraicos: concreto, axiomático y universal.

Nivel de Concreto

Casi todas las matemáticas que has hecho en el pasado estaban a nivel concreto. Por regla general, si puedes dar ejemplos de algunos elementos típicos del dominio y describir cómo actúan las operaciones sobre ellos, estás describiendo un sistema algebraico concreto. Dos ejemplos de sistemas de concreto son$B^*$ y$M_{2\times 2}(\mathbb{R})\text{.}$ algunos otros son:

Los enteros con suma. Por supuesto, la adición no es la única operación estándar que podríamos incluir. Técnicamente, si fuéramos a sumar multiplicación, tendríamos un sistema diferente.
Los subconjuntos de los números naturales, con unión, intersección y complementación.
Los números complejos con suma y multiplicación.

Nivel Axiomático

El siguiente nivel de abstracción es el nivel axiomático. En este nivel, no se especifican los elementos del dominio, pero se enuncian ciertos axiomas sobre el número de operaciones y sus propiedades. El sistema que llamamos$M$ es un sistema axiomático. Algunas combinaciones de axiomas son tan comunes que se le da un nombre a cualquier sistema algebraico al que se aplican. Cualquier sistema con las propiedades de$M$ se llama monoide. El estudio de se$M$ llamaría teoría monoide. Los supuestos que hicimos sobre la$M\text{,}$ asociatividad y la existencia de una identidad, se denominan axiomas monoides. Uno de tus pocos pinceles con el nivel axiomático puede haber estado en tu curso de álgebra elemental. Muchos textos de álgebra identifican las propiedades de los números reales con suma y multiplicación como los axiomas de campo. Como veremos en el Capítulo 16, “Anillos y Campos”, los números reales comparten estos axiomas con otros sistemas concretos, todos los cuales se llaman campos.

Nivel Universal

El nivel final de abstracción es el nivel universal. Existen ciertos conceptos, llamados conceptos de álgebra universal, que se pueden aplicar al estudio de todos los sistemas algebraicos. Si bien un enfoque puramente universal del álgebra sería demasiado abstracto para nuestros propósitos, definir conceptos a este nivel debería facilitar la organización de las diversas teorías algebraicas en tu propia mente. En este capítulo, consideraremos los conceptos de isomorfismo, subsistema y producto directo.

Grupos

Para ilustrar el nivel axiomático y los conceptos universales, consideraremos otro tipo de sistema axiomático, el grupo. En el Capítulo 5 notamos que la ecuación más simple en álgebra matricial que a menudo se nos llama a resolver es$A X = B\text{,}$ dónde$A$ y$B$ se conocen matrices cuadradas y$X$ es una matriz desconocida. Para resolver esta ecuación, necesitamos las leyes asociativas, de identidad e inversas. Llamamos a los sistemas que tienen estas propiedades grupos.

Definición $\PageIndex{1}$: Group

Un grupo consiste en un conjunto no vacío$G$ y una operación$*$ binaria para$G$ satisfacer las propiedades

$*$es asociativo$G\text{:}$$(a*b)*c=a*(b*c)$ para todos$a, b, c \in G\text{.}$
Existe un elemento de identidad,$e \in G\text{,}$ tal que$a*e=e*a=a$ para todos$a \in G\text{.}$
Por todo$a \in G\text{,}$ existe una inversa; es decir, existe$b\in G$ tal que$a *b = b*a=e\text{.}$

Un grupo suele ser denotado por el nombre de su conjunto,$G\text{,}$ u ocasionalmente por$[G; * ]$ para enfatizar la operación. A nivel concreto, la mayoría de los conjuntos tienen una operación estándar asociada a ellos que formará un grupo. Como veremos a continuación, los enteros con suma es un grupo. Por lo tanto, en la teoría de grupos$\mathbb{Z}$ siempre representa$[\mathbb{Z}; +]\text{.}$

Nota$\PageIndex{1}$: Generic Symbols

A nivel axiomático y universal, a menudo hay símbolos que tienen un significado especial unido a ellos. En la teoría de grupos, la letra$e$ se utiliza para denotar el elemento de identidad de cualquier grupo que se esté discutiendo. Un poco más tarde, probaremos que la inversa de un elemento de grupo,$a\text{,}$ es única y su inversa suele denotarse$a^{-1}$ y se lee “$a$inversa”. Cuando se discute un grupo concreto, estos símbolos se dejan caer en favor de símbolos concretos. Estos símbolos concretos pueden o no ser similares a los símbolos genéricos. Por ejemplo, el elemento de identidad del grupo de enteros es 0, y la inversa de$n$ se denota por$-n\text{,}$ la inversa aditiva de$n\text{.}$

El asterisco también podría considerarse un símbolo genérico ya que se utiliza para denotar operaciones a nivel axiomático.

Ejemplo$\PageIndex{2}$: Some Concrete Groups

Los enteros con suma es un grupo. Sabemos que la adición es asociativa. Cero es la identidad para la suma:$0 + n = n + 0 = n$ para todos$n\text{.}$ los enteros El inverso aditivo de cualquier entero se obtiene negándolo. Por lo tanto, la inversa de$n$ es$-n\text{.}$
Los enteros con multiplicación no es un grupo. Aunque la multiplicación es asociativa y 1 es la identidad para la multiplicación, no todos los enteros tienen una inversa multiplicativa en$\mathbb{Z}\text{.}$ Por ejemplo, la inversa multiplicativa de 10 es$\frac{1}{10}\text{,}$ pero no$\frac{1}{10}$ es un entero.
El conjunto de potencia de cualquier conjunto$U$ con la operación de diferencia simétrica,$\oplus\text{,}$ es un grupo. Si$A$ y$B$ son conjuntos, entonces lo$A\oplus B=(A\cup B)-(A\cap B)\text{.}$ dejaremos al lector probar que$\oplus$ es asociativo sobre$\mathcal{P}(U)\text{.}$ La identidad del grupo es el conjunto vacío:$A\oplus \emptyset = A\text{.}$ Cada conjunto es su propio inverso ya que$A \oplus A = \emptyset\text{.}$ Note que no$\mathcal{P}(U)$ es un grupo con unión o intersección .

Definición$\PageIndex{2}$: Abelian Group

Un grupo es abeliano si su operación es conmutativa.

Nota$\PageIndex{2}$: Abel

La mayoría de los grupos que discutiremos en este libro serán abelianos. El término abeliano se utiliza para honrar al matemático noruego N. Abel (1802-29), quien ayudó a desarrollar la teoría de grupos.

$clipboard_e32d6b98b684bc0867985c4949e8576ba.png$ Figura$\PageIndex{1}$: Sello noruego honrando a Abel

Ejercicios

Ejercicio$\PageIndex{1}$

Discutir la analogía entre los términos genérico y concreto para sistemas algebraicos y los términos genérico y comercio para medicamentos recetados.

Contestar: Los términos “genérico” y “comercio” para los medicamentos recetados son análogos a los sistemas algebraicos “genéricos” y “concretos”. La aspirina genérica, por ejemplo, no tiene nombre, mientras que Bayer, Tylenol, Tampina y Anacina son todos tipos comerciales o específicos de aspirinas. Lo mismo puede decirse de un grupo genérico$[G; *]$ donde$G$ es un conjunto no vacío y$*$ es una operación binaria en$G\text{,}$ Cuando se pueden dar ejemplos de elementos de dominio típicos junto con descripciones de cómo actúan las operaciones sobre ellos, como$\mathbb{Q}$ * o$M_{2\times 2}(\mathbb{R})\text{,}$ entonces el sistema es concreto (tiene un nombre específico, como ocurre con la aspirina). Genérico es una manera de describir un sistema algebraico general, mientras que un sistema concreto tiene un nombre o símbolos que lo hacen distinguible de otros sistemas.

Ejercicio$\PageIndex{2}$

Discutir la conexión entre grupos y monoides. ¿Cada monoide es un grupo? ¿Cada grupo es monoide?

Ejercicio$\PageIndex{3}$

¿Cuáles de los siguientes son grupos?

$B^*$con concatenación (ver Subsección 11.2.1).
$M_{2\times 3}(\mathbb{R})$con adición de matriz.
$M_{2\times 3}(\mathbb{R})$con multiplicación matricial.
Los números reales positivos,$\mathbb{R}^+\text{,}$ con multiplicación.
Los números reales distintos de cero,$\mathbb{R}^*\text{,}$ con multiplicación.
$\{1, -1\}$con multiplicación.
Los enteros positivos con la operación$M$ definida por$a M b = \textrm{ the larger of } a \textrm{ and } b\text{.}$

Contestar: Los sistemas en las partes b, d, e y f son grupos.

Ejercicio$\PageIndex{4}$

Demostrar que,$\oplus\text{,}$ definido por$A \oplus B = (A \cup B) - (A \cap B)$ es una operación asociativa sobre$\mathcal{P}(U)\text{.}$

Ejercicio $\PageIndex{5}$

El siguiente problema proporciona un ejemplo de un grupo no abeliano. Una matriz de gradas es una matriz que tiene solo 0's y 1's como entradas de tal manera que cada fila tiene exactamente un 1 y cada columna tiene exactamente un 1. El término matriz de gradas se deriva del hecho de que cada matriz de gradas representa la colocación de$n$ gradas en un$n\times n$ tablero de ajedrez de tal manera que ninguna de las gradas puede atacarse entre sí. Una grada en el ajedrez solo puede moverse vertical u horizontalmente, pero no diagonalmente. Dejado$R_n$ ser el conjunto de matrices$n\times n$ de torres. Hay seis matrices$3\times 3$ de gradas:

$\begin{array}{ccc} I=\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right) & R_1=\left( \begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ \end{array} \right) & R_2=\left( \begin{array}{ccc} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{array} \right) \\ F_1=\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{array} \right) & F_2=\left( \begin{array}{ccc} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ \end{array} \right) & F_3=\left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} \right) \\ \end{array}$

Enumere$2\times 2$ las matrices de gradas. Forman un grupo,$R_2,$ bajo multiplicación matricial. Escribe la tabla de multiplicación. ¿El grupo es abeliano?
Escribe la tabla de multiplicación para$R_3$. Este es otro grupo. ¿Es abeliano?
¿Cuántas$4\times 4$ matrices de gradas hay? ¿Cuántas$n\times n$ matrices de gradas hay?

Contestar

Los elementos son$I=\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right)\text{,}$ y$T=\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array} \right)\text{,}$ el grupo es abeliano. La mesa de operaciones es$\begin{array}{c|cc} \cdot & I & T\\ \hline I & I & T\\ T & T & I\\ \end{array}$
\ begin {ecuation*}\ begin {array} {c|c} &\ begin {array} {cccccc} I & R_1 & R_2 & F_1 & F_2 & F_3\\ end {array}\\\ hline\ begin {array} {c} I\\ R_1\\ R_2\\ F_1\\ F_2\\ F_3\\ end {array} &\ begin {array} {cccccc} I & R_1 & R_2 & F_1 & F_2 & F_3\\ R_1 & R_2 & I & F_2 & F_3 & F_1\\ R_2 & I & R_1 & F_3 & F_1 & F_2\\ F_1 & F & F_2 & I & R_2 & R_1\ F_2 & F_1 & F_3 & R_1 & I & R_2\\ F_3 y F_2 & F_1 y R_1 & I\\\ end {array}\\\ end {array}\ end {ecuación*}
Este grupo no es abeliano ya que, por ejemplo,$F_1 F_2=R_2$ y$F_2 F_1=R_2\text{.}$
¡4! = 24,$n!\text{.}$

Ejercicio$\PageIndex{6}$

Para cada uno de los siguientes conjuntos, identifique la operación estándar que da como resultado un grupo. ¿Cuál es la identidad de cada grupo?

El conjunto de todas las$2\times 2$ matrices con entradas reales y determinantes distintos de cero.
El conjunto de$2 \times 3$ matrices con entradas racionales.

Ejercicio$\PageIndex{7}$

$V = \{e,a,b, c\}\text{.}$Let$*$ Ser definido (parcialmente) por$x * x = e$ para todos$x \in V\text{.}$ Escribe una tabla completa para$*$ así que$[V; * ]$ sea un grupo.

Contestar: La identidad es$e\text{.}$$a*b = c\text{,}$$a*c= b\text{,}$$b*c = a\text{,}$ y$[V; *]$ es abeliana. (Este grupo se llama comúnmente el grupo Klein-4.)

Ejercicio$\PageIndex{8}$

Considera el siguiente conjunto de seis expresiones algebraicas, cada una definiendo una función sobre el conjunto de números reales excluyendo los números 0 y 1.

\ begin {ecuación*}\ mathcal {H} =\ izquierda\ {x,1-x,\ frac {1} {1-x},\ frac {1} {x},\ frac {x-1} {x},\ frac {x} {x-1}\ derecha\} =\ izquierda\ {y_1, y_2, y_3, y_4, y_5, y_6\ derecha\}\ end {ecuación*}

Podemos operar en cualquiera de estas expresiones usando la composición de funciones. Por ejemplo,

\ begin {ecuación*} (y_3\ circ y_4) (x) = y_3 (y_4 (x)) =y_3 (\ frac {1} {x}) =\ frac {1} {1-\ frac {1} {x}} =\ frac {x} {x-1} =y_6 (x)\ end {ecuación*}

Por lo tanto,$y_3 \circ y_4 = y_6\text{.}$ complete la siguiente tabla de operaciones para la composición de funciones en$\mathcal{H}\text{.}$

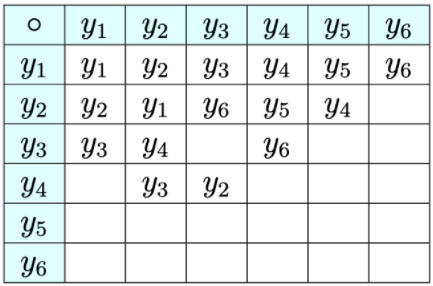$clipboard_efd5ebb330aa81769eacb4a33c172cea2.png$ Figura$\PageIndex{2}$: Mesa de operaciones parcialmente terminada para$\mathcal{H}$

¿Es$[\mathcal{H},\circ]$ un monoide? ¿Es un grupo?

Contestar: Sí, este es un grupo. Es posible que veas algunas similitudes con el grupo de tres por tres matrices de torres.