11.5: Subsistemas

Última actualización
Guardar como PDF

Page ID: 117319

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Definición

El subsistema es un concepto fundamental de álgebra a nivel universal.

Definición $\PageIndex{1}$: Subsystem

Si$\left[V; *_1, \ldots ,*_n\right]$ es un sistema algebraico de cierto tipo y$W$ es un subconjunto de$V\text{,}$ entonces$W$ es un subsistema de$V$ si$\left[W; *_1, \ldots ,*_n\right]$ es un sistema algebraico del mismo$V\text{.}$ tipo que La notación habitual para “$W$es un subsistema de$V$” es$W \leq V\text{.}$

Dado que la definición de subsistema está a nivel universal, podemos citar ejemplos del concepto de subsistemas tanto a nivel axiomático como concreto.

Ejemplo$\PageIndex{1}$: Examples of Subsystems

(Axiomático) Si$[G; *]$ es un grupo, y$H$ es un subconjunto de$G\text{,}$ entonces$H$ es un subgrupo de$G$ si$[H; *]$ es un grupo.
(Concreto)$U = \{-1,1\}$ es un subgrupo de$\left[\mathbb{R}^*;\cdot \right]\text{.}$ Tómese el tiempo ahora para escribir la tabla de multiplicación de$U$ y convencerse de que$[U;\cdot ]$ es un grupo.
(Concreto) Los enteros pares,$2\mathbb{Z} = \{2k : k \textrm{ is} \textrm{ an} \textrm{ integer}\}$ es un subgrupo de$[\mathbb{Z}; +]\text{.}$ Convénzate de este hecho.
(Concreto) El conjunto de enteros no negativos no es un subgrupo de$[\mathbb{Z}; +]\text{.}$ Todos los axiomas del grupo son verdaderos para este subconjunto excepto uno: ningún entero positivo tiene un inverso aditivo positivo. Por lo tanto, la propiedad inversa no es cierta. Tenga en cuenta que cada axioma grupal debe ser cierto para que un subconjunto sea un subgrupo.
(Axiomático) Si$M$ es un monoide y$P$ es un subconjunto de$M\text{,}$ entonces$P$ es un submonoide de$M$ si$P$ es un monoide.
(Concreto) Si$B^*$ es el conjunto de cadenas de 0 y 1 de longitud cero o más con la operación de concatenación, entonces dos ejemplos de submonoides de$B^*$ son: (i) el conjunto de cadenas de longitud par, y (ii) el conjunto de cadenas que no contienen 0's El conjunto de cadenas de longitud menor a 50 no es un submonoide porque no está cerrado bajo concatenación. ¿Por qué el conjunto de cadenas de longitud 50 o más no es un submonoide de$B^*\text{?}$

Subgrupos

Para lo que resta de esta sección, nos concentraremos en las propiedades de los subgrupos. El primer orden del día es establecer una forma sistemática de determinar si un subconjunto de un grupo es un subgrupo.

Teorema$\PageIndex{1}$: Subgroup Conditions

Para determinar si H, un subconjunto de grupo$[G;*]\text{,}$ es un subgrupo, basta con probar:

H se cierra bajo$*\text{;}$ eso es decir,$a, b \in H \Rightarrow a * b \in H\text{;}$
H contiene el elemento de identidad para$*\text{;}$ y
H contiene la inversa de cada uno de sus elementos; es decir,$a\in H \Rightarrow a^{-1}\in H\text{.}$

Prueba: Nuestra prueba consiste en verificar que si las tres propiedades anteriores son verdaderas, entonces todos los axiomas de un grupo son ciertos para$[H ; *]\text{.}$ Por Condición (a),$*$ pueden considerarse una operación sobre$H\text{.}$ Las propiedades asociativas, identitarias e inversas son los axiomas que se necesitan. La identidad y las propiedades inversas son verdaderas por las condiciones (b) y (c), respectivamente, dejando sólo la propiedad asociativa. Ya que,$[G; *]$ es un grupo,$a * (b * c) = (a * b) * c$ para todos$a, b, c \in G\text{.}$ Ciertamente, si esta ecuación es verdadera para todas las elecciones de tres elementos a partir de$G\text{,}$ ella será cierto para todas las elecciones de tres elementos$H\text{,}$ desde que$H$ es un subconjunto de$G\text{.}$

Por cada grupo con al menos dos elementos, hay al menos dos subgrupos: son todo el grupo y$\{e\}\text{.}$ Dado que estos dos son automáticos, no se consideran muy interesantes y se les llama los subgrupos impropios del grupo; a veces$\{e\}$ se le conoce como el subgrupo trivial. Todos los demás subgrupos, si los hay, se denominan subgrupos propios.

Podemos aplicar el Teorema tanto$\PageIndex{1}$ a nivel concreto como axiomático.

Ejemplo$\PageIndex{2}$: Applying Conditions for a Subgroup

(Concreto) Podemos verificar eso$2\mathbb{Z} \leq \mathbb{Z}\text{,}$ como se indica en Ejemplo$\PageIndex{1}$. Siempre que quieras discutir un subconjunto, debes encontrar alguna manera conveniente de describir sus elementos. Un elemento de se$2\mathbb{Z}$ puede describir como 2 veces un entero; es decir,$a \in 2\mathbb{Z}$ es equivalente a$(\exists k)_{\mathbb{Z}}(a = 2k)\text{.}$ Ahora podemos verificar que las tres condiciones del Teorema$\PageIndex{1}$ son verdaderas para 2$\mathbb{Z}\text{.}$ Primero, si$a, b \in 2\mathbb{Z}\text{,}$ entonces existen$j, k \in \mathbb{Z}$ tal que$a = 2j$ y$b = 2k\text{.}$ Un error común es escribir algo así como$a=2j$ y$b=2j\text{.}$ Esto significaría aquello$a=b\text{,}$ que no necesariamente es cierto. Es por ello que se necesitan dos variables distintas para describir$a$ y$b\text{.}$ Volviendo a nuestra prueba, podemos agregar$a$ y$b\text{:}$$a + b = 2j + 2k = 2(j + k)\text{.}$ Dado que$j + k$ es un entero,$a + b$ es un elemento de$2\mathbb{Z}\text{.}$ Segundo, la identidad,$0\text{,}$ pertenece a 2$\mathbb{Z}$ ( $0 = 2(0)$). Por último, si$a \in 2\mathbb{Z}$$a = 2k, -a = -(2k) = 2(-k)\text{,}$ y$-a \in 2\mathbb{Z}\text{.}$ por$-k\in \mathbb{Z}\text{,}$ lo tanto, Por teorema$\PageIndex{1}$,$2\mathbb{Z} \leq \mathbb{Z}\text{.}$ ¿Cómo cambiaría este argumento si se le pidiera probar eso$3\mathbb{Z} \leq \mathbb{Z}\text{?}$ o$n \mathbb{Z} \leq \mathbb{Z}, n \geq 2\text{?}$
(Concreto) Podemos probar que$H = \{0, 3, 6, 9\}$ es un subgrupo de$\mathbb{Z}_{12}\text{.}$ Primero, por cada par ordenado$(a, b) \in H \times H\text{,}$$a +_{12} b$ está en$H\text{.}$ Esto se puede verificar sin demasiados problemas ya que$\left| H \times H\right| = 16\text{.}$ así podemos concluir que$H$ se cierra bajo$+_{12}\text{.}$ Segundo,$0\in H\text{.}$ Tercero,$-0 = 0\text{,}$ $-3 = 9\text{,}$$-6 = 6\text{,}$y$-9 = 3\text{.}$ Por lo tanto, la inversa de cada elemento de$H$ está en$H\text{.}$
(Axiomático) Si$H$ y$K$ son ambos subgrupos de un grupo$G\text{,}$ entonces$H \cap K$ es un subgrupo de$G\text{.}$ Para justificar esta afirmación, no tenemos información concreta con la que trabajar, solo los hechos que$H \leq G$ y$K \leq G\text{.}$ Nuestra prueba que$H \cap K \leq G$ refleja esto y es un ejercicio de aplicando las definiciones de intersección y subgrupo, (i) Si$a$ y$b$ son elementos de$H \cap K\text{,}$ entonces$a$ y$b$ ambos pertenecen$H\text{,}$ y desde$H \leq G\text{,}$$a * b$ deben ser un elemento de$H\text{.}$ Similarmente,$a * b \in K\text{;}$ por lo tanto,$a * b \in H \cap K\text{.}$ (ii) El identidad de$G$ debe pertenecer a ambos$H$ y$K\text{;}$ por lo tanto pertenece a$H \cap K\text{.}$ (iii) Si$a \in H \cap K\text{,}$ entonces$a \in H\text{,}$ y desde$H \leq G\text{,}$$a^{-1}\in H\text{.}$ Similarmente, De$a^{-1}\in K\text{.}$ ahí, por el teorema,$H \cap K \leq G\text{.}$ Ahora que se ha establecido este hecho, podemos aplicarlo a cualquier par de subgrupos de cualquier grupo. Por ejemplo, ya que$2\mathbb{Z}$ y$3\mathbb{Z}$ son ambos subgrupos de$[\mathbb{Z};+]\text{,}$$2\mathbb{Z} \cap 3\mathbb{Z}$ es también un subgrupo de$\mathbb{Z}\text{.}$ Nota que si$a \in 2\mathbb{Z} \cap 3\mathbb{Z}\text{,}$$a$ debe tener un factor de 3; es decir, existe$k\in \mathbb{Z}$ tal que$a = 3k\text{.}$ además,$a$ debe ser par, por lo tanto $k$debe ser parejo. Existe$j \in \mathbb{Z}$ tal que$k = 2j\text{,}$ por lo tanto$a = 3(2j)= 6j\text{.}$ Esto demuestra que$2\mathbb{Z}\cap 3\mathbb{Z}\subseteq 6\mathbb{Z}\text{.}$ La contención opuesta se puede establecer fácilmente; por lo tanto,$2\mathbb{Z} \cap 3\mathbb{Z} = 6\mathbb{Z}\text{.}$

Dado un grupo finito, podemos aplicar el Teorema 11.3.10 para obtener una condición más simple para que un subconjunto sea un subgrupo.

Teorema $\PageIndex{2}$: Condition for a Subgroup of Finite Group

Dado que$[G; * ]$ es un grupo finito y$H$ es un subconjunto no vacío de$G\text{,}$ if$H$ está cerrado bajo$*$, entonces$H$ es un subgrupo de$G\text{.}$

Prueba

En esta prueba, demostramos que las Condiciones (b) y (c) del Teorema se$\PageIndex{1}$ derivan del cierre de$H$ bajo la$*\text{,}$ cual se encuentra la condición (a) del teorema. Primero, seleccione cualquier elemento de$H\text{;}$ llamarlo$\beta\text{.}$ Los poderes de$\beta$:$\beta ^1\text{,}$$\beta ^2\text{,}$$\beta^3,\ldots$ están todos adentro$H$ por la propiedad de cierre. Por el Teorema 11.3.10, existe$m\text{,}$$m\leq \left| G\right|\text{,}$ tal que de$\beta ^m = e\text{;}$ ahí$e \in H\text{.}$ Para probar que (c) es cierto, dejamos$a$ ser cualquier elemento de$H\text{.}$ Si$a = e\text{,}$ entonces$a^{-1}$ está en$H$ ya$e^{-1} = e\text{.}$ Si$a\neq e\text{,}$$a^q=e$ para algunos $q$entre 2 y$\left| G\right|$ y

\ begin {ecuación*} e = a^q = a ^ {q-1} * a\ end {ecuación*}

Por lo tanto$a^{-1}= a^{q-1}$,, que pertenece a$H$ desde$q - 1 \geq 1\text{.}$

Nota - Aplicar la condición para un subgrupo de un grupo finito

Para determinar si$H_1= \{0, 5, 10\}$ y$H_2 = \{0, 4, 8, 12\}$ son subgrupos de solo$\mathbb{Z}_{15}\text{,}$ necesitamos escribir las tablas de suma (módulo 15) para estos conjuntos. Esto es fácil de hacer con un poco de código Sage que incluimos a continuación y luego para cualquier módulo y subconjunto, podemos generar el cuerpo de una tabla de adición. El código está configurado para$H_1$, pero se puede ajustar fácilmente para$H_2\text{.}$

def addition_table(n,H):
    for a in H:
        line=[]
        for b in H:
            line+=[(a+b)%n]
        print(line)
addition_table(15,Set([0,5,10]))

Tenga en cuenta que$H_1$ es un subgrupo de$\mathbb{Z}_{15}\text{.}$ Dado que el interior de la tabla de suma para$H_2$ contiene elementos que están fuera de no$H_2\text{,}$$H_2$ es un subgrupo de$\mathbb{Z}_{15}\text{.}$

Subgrupos cíclicos

Un tipo de subgrupo que merece mención especial por su simplicidad es el subgrupo cíclico.

Definición $\PageIndex{2}$: Cyclic Subgroup

Si$G$ es un grupo y$a \in G\text{,}$ el subgrupo cíclico generado por$a\text{,}$$\langle a \rangle\text{,}$ es el conjunto de todas las potencias de$a\text{:}$

\ begin {ecuación*}\ langle a\ rangle =\ izquierda\ {a^n: n\ in\ mathbb {Z}\ derecha\}\ texto {.} \ end {ecuación*}

Nos referimos$a$ como un generador de subgrupo$\langle a \rangle\text{.}$

Un subgrupo$H$ de un grupo$G$ es cíclico si existe$a \in H$ tal que$H = \langle a \rangle\text{.}$

Nota$\PageIndex{1}$

Si la operación$G$ es aditiva, entonces$\langle a \rangle = \{(n)a : n \in \mathbb{Z}\}\text{.}$

Definición $\PageIndex{3}$: Order of a Group Element

El orden de un elemento$a$ de grupo$G$ es el número de elementos en el subgrupo cíclico de$G$ generado por$a\text{.}$ El orden de$a$ se denota$ord(a)\text{.}$

Ejemplo$\PageIndex{3}$

En$[\mathbb{R}^* ; \cdot ]\text{,}$$\langle 2 \rangle = \left\{2^n : n \in \mathbb{Z}\right\} = \left\{\ldots ,\frac{1}{16}, \frac{1}{8} ,\frac{1}{4}, \frac{1}{2}, 1, 2, 4, 8, 16,\ldots \right\}\text{.}$
En$\mathbb{Z}_{15}\text{,}$$\langle 6 \rangle = \{0, 3, 6, 9, 12\}\text{.}$ Si$G$ es finito, es necesario enumerar solo los poderes positivos (o múltiplos) de$a$ hasta la primera ocurrencia de la identidad para obtener todos los$\langle a \rangle\text{.}$ In$\mathbb{Z}_{15}$, los múltiplos de 6 son 6,$(2)6 = 12\text{,}$$(3)6=3\text{,}$$(4)6=9\text{,}$ y$(5)6 = 0\text{.}$ Tenga en cuenta que$\{0, 3, 6, 9, 12\}$ es también$\langle 3 \rangle\text{,}$$\langle 9 \rangle\text{,}$ y$\langle 12 \rangle\text{.}$ Esto demuestra que un subgrupo cíclico puede tener diferentes generadores.

Si quieres enumerar los subgrupos cíclicos de un grupo, el siguiente teorema te puede ahorrar algo de tiempo.

Teorema$\PageIndex{3}$

Si$a$ es un elemento de grupo$G\text{,}$ entonces$\langle a \rangle = \langle a^{-1}\rangle\text{.}$

Esta es una manera fácil de ver, por ejemplo, que$\langle 9 \rangle$ en$\mathbb{Z}_{15}$ iguales$\langle 6 \rangle\text{,}$ desde$-6 = 9\text{.}$

Ejercicios

Ejercicio$\PageIndex{1}$

¿Cuál de los siguientes subconjuntos de los números reales es un subgrupo de$[\mathbb{R}; +]\text{?}$

los números racionales
los números reales positivos
$\displaystyle \{k/2 \mid k \textrm{ is} \textrm{ an} \textrm{ integer}\}$
$\displaystyle \{2^k \mid k \textrm{ is an integer}\}$
$\displaystyle \{x \mid -100 \leq x \leq 100\}$

Contestar: Sólo a y c son subgrupos.

Ejercicio$\PageIndex{2}$

Describir en términos más simples los siguientes subgrupos de$\mathbb{Z}\text{:}$

$\displaystyle 5\mathbb{Z} \cap 4\mathbb{Z}$
$4\mathbb{Z} \cap 6\mathbb{Z}$(tenga cuidado)
el único subgrupo finito de$\mathbb{Z}$

Ejercicio$\PageIndex{3}$

Encuentra al menos dos subgrupos propios de$R_3$, el conjunto de matrices de$3\times 3$ Torre (ver Ejercicio 11.2.5).

Contestar: $\left\{I,R_1,R_2\right\}\text{,}$$\left\{I,F_1\right\}\text{,}$$\left\{I,F_2\right\}\text{,}$y$\left\{I,F_3\right\}$ son todos los subgrupos propios de$R_3\text{.}$

Ejercicio$\PageIndex{4}$

¿Dónde se debe colocar lo siguiente en la Figura$\PageIndex{1}$?

$\displaystyle e$
$\displaystyle a^{-1}$
$\displaystyle x * y$

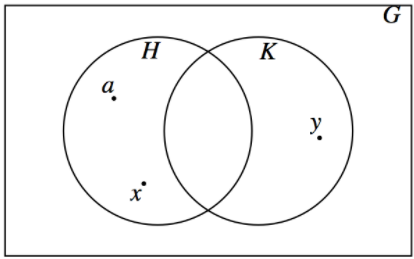$clipboard_e9be593915a7943877ecfe3df9dfc343a.png$ Figura$\PageIndex{1}$: Figura para el ejercicio$\PageIndex{4}$

Ejercicio$\PageIndex{5}$

Enumere los subgrupos cíclicos de$\mathbb{Z}_6$ y dibuje un diagrama de orden para la relación “es un subconjunto de” en estos subgrupos.
Haz lo mismo para$\mathbb{Z}_{12}\text{.}$
Haz lo mismo para$\mathbb{Z}_8\text{.}$
Sobre la base de tus resultados en las partes a, b y c, ¿qué esperarías si hicieras lo mismo con$\mathbb{Z}_{24}\text{?}$

Contestar

$\langle 1\rangle = \langle 5\rangle = \mathbb{Z}_6\text{,}$$\quad$$\langle 2\rangle = \langle 4\rangle = \{2, 4, 0\}\text{,}$$\langle 3\rangle = \{3, 0\}\text{,}$$\langle 0\rangle = \{0\}$
$\langle 1\rangle = \langle 5\rangle = \langle 7\rangle = \langle 11\rangle =\mathbb{Z}_{12}\text{,}$$\langle 2\rangle = \langle 10\rangle = \{2, 4, 6, 8, 10, 0\}\text{,}$$\langle 3\rangle = \langle 9\rangle = \{3, 6, 9, 0\}\text{,}$$\langle 4\rangle = \langle 8 \rangle = \{ 4 , 8, 0\}\text{,}$$\langle 6\rangle = \{6, 0\}\text{,}$$\langle 0\rangle = \{0\}$
$\langle 1\rangle = \langle 3\rangle = \langle 5 \rangle = \langle 7\rangle = \mathbb{Z}_8\text{,}$$\langle 2\rangle = \langle 6\rangle = \{2, 4, 6, 0\}\text{,}$$\langle 4\rangle = \{4, 0\}\text{,}$$\langle 0\rangle = \{0\}$
Con base en los diagramas de orden para las partes de la a a a la c en la Figura$\PageIndex{2}$, esperaríamos ver un diagrama de orden similar al de las divisiones en$\{1, 2, 3, 4, 6, 8, 12, 24\}$ (los divisores de 24) si examináramos los subgrupos de$\mathbb{Z}_{24}\text{.}$ Este es efectivamente el caso.

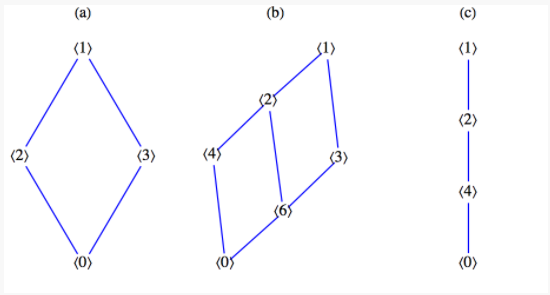$clipboard_e32c77ed2b48c57ce416ea3c460f358f9.png$ Figura$\PageIndex{2}$: Figura para el ejercicio$\PageIndex{5}$

Ejercicio$\PageIndex{6}$: Subgroups Generated by Subsets of a Group

El concepto de subgrupo cíclico es un caso especial del concepto que discutiremos aquí. Dejar$[G; * ]$ ser un grupo y$S$ un subconjunto no vacío de$G\text{.}$ Definir el conjunto$\langle S \rangle$ recursivamente por:

Si$a\in S\text{,}$ entonces$a\in \langle S \rangle\text{.}$
Si$a, b \in \langle S \rangle\text{,}$ entonces$a * b \in \langle S \rangle\text{,}$ y
Si$a \in \langle S \rangle\text{,}$ entonces$a^{-1}\in \langle S \rangle\text{.}$

Por su definición,$\langle S \rangle$ tiene todas las propiedades necesarias para ser un subgrupo de$G\text{.}$ Lo único que no es obvio es que la identidad de$G$ está en$\langle S \rangle\text{.}$ Demostrar que la identidad de$G$ está en$\langle S \rangle\text{.}$
Lo que hay$\langle\{9, 15\}\rangle$ en$[\mathbb{Z}; +]\text{?}$
Demostrar que si$H \leq G$ y$S \subseteq H\text{,}$ entonces$\langle S \rangle\leq H\text{.}$ Esto prueba que$\langle S \rangle$ está contenido en cada subgrupo de$G$ lo$S\text{;}$ que contiene es decir,$\langle S \rangle =\underset{S\subseteq H, H\leq G}{\cap }H\text{.}$
Describir$\langle \{0.5, 3\}\rangle $ en$\left[ \mathbb{R}^+;\cdot \right]$ y en$[\mathbb{R}; +]\text{.}$
Si$j, k \in \mathbb{Z}\text{,}$$\langle\{j,k\}\rangle$ es un subgrupo cíclico de$\mathbb{Z}\text{.}$ En términos de$j$ y$k\text{,}$ qué es un generador de$\langle \{j, k\}\rangle \text{?}$

Ejercicio$\PageIndex{7}$

Demostrar que si$H,K \leq G\text{,}$ y$H\cup K=G\text{,}$ entonces$H = G$ o$K = G\text{.}$

Pista

Usa un argumento indirecto.

Contestar

Supongamos que$H$ y$K$ son subgrupos de grupo$G\text{,}$ y que, como en Figura$\PageIndex{1}$, hay elementos$x \in H - K$ y$y \in K - H\text{.}$ Considera el producto$x * y\text{.}$ ¿Dónde podría colocarse en el diagrama de Venn? Si podemos probar que debe estar en la región exterior,$H^c \cap K^c=(H \cup K)^c\text{,}$ entonces hemos probado que no$H \cup K$ está cerrado bajo$*$ y no puede ser un subgrupo de$G\text{,}$ Supongamos que$x*y\in H\text{.}$ Since$x$ está en$H\text{,}$$x^{-1}$ está en$H$ y así por cierre$x^{-1}*(x * y )= y \in H$ que es un contradicción. Del mismo modo,$x*y \notin K\text{.}$

Una manera de interpretar este teorema es que ningún grupo es la unión de dos grupos.

Ejercicio$\PageIndex{8}$

Demostrar que el orden de un elemento,$a$ de un grupo es el número entero menos positivo,$k\text{,}$ tal que$a^k$ es la identidad del grupo.