11.6: Productos Directos

Definición

Nuestro segundo concepto algebraico universal nos permite mirar en dirección opuesta a los subsistemas. Los productos directos nos permiten crear sistemas más grandes. En la siguiente definición, evitamos complicar la notación al no especificar cuántas operaciones tienen los sistemas.

Definición \(\PageIndex{1}\): Direct Product

Si\(\left[V_i;*_i, \diamond_i, \ldots \right]\text{,}\)\(i = 1, 2, \ldots, n\) son sistemas algebraicos del mismo tipo, entonces el producto directo de estos sistemas es\(V =V_1\times V_2\times \cdots \times V_n\), con operaciones definidas a continuación. Los elementos de\(V\) son\(n\) -tuplas de\(a_k \in V_k\text{,}\)\(k = 1, \dots , n\text{.}\) la forma\(\left(a_1, a_2, \dots , a _n \right)\text{,}\) donde\(V_1\text{,}\)\(V_2, \dots, V_n\) Los sistemas se llaman los factores de\(V\text{.}\) Hay tantas operaciones en\(V\) como hay en los factores. Cada una de estas operaciones se define por componentes:

Si\(\left(a_1, a_2, . . . , a _n \right), \left(b_1,b_2, . . . , b _n \right)\in V\text{,}\)

\ begin {ecuación*}\ begin {array} {c}\ left (a_1, a_2,\ dots, a_n\ right) *\ left (b_1, b_2,\ dots, b_n\ right) =\ left (a_1 *_1 b_1, a_2 *_2 b_2,\ ldots, a_n *_n b_n\ right)\\ left (a_1, a_2,\ puntos, a_n\ derecha)\ diamante\ izquierda (b_1, b_2,\ puntos, b_n\ derecha) =\ izquierda (a_1\ diamante_1 b_1, a_2\ diamante_2 b_2,\ puntos, a_n\ diamante_n b_n\ derecha)\\\ textrm {etc.}\\\\ final {matriz}\ final {ecuación*}

Ejemplo\(\PageIndex{1}\): A Direct Product of Monoids

Considera los monoides\(\mathbb{N}\) (el conjunto de números naturales con suma) y\(B^*\) (el conjunto de cadenas finitas de 0's y 1's con concatenación). El producto directo de\(\mathbb{N}\) con\(B^*\) es un monoide. Ilustramos su funcionamiento, que denotaremos\(*\text{,}\) con ejemplos:

\ begin {ecuación*}\ begin {array} {c} (4, 001) * (3, 11) = (4 + 3, 001+11) = (7, 00111)\\ (0, 11010) * (3,01) = (3, 1101001)\\ (0,\ lambda) * (129, 00011) = (0 + 129,\ lambda +00011) = (129, 00011)\\ (2, 01) * (8, 10) = (10,0110)\ textrm {, y}\\ (8, 10) * (2, 01) = (10, 1001)\ end {array}\ end {ecuación*}

Tenga en cuenta que nuestro nuevo monoide no es conmutativo. ¿Para qué sirve la identidad\(*\)?

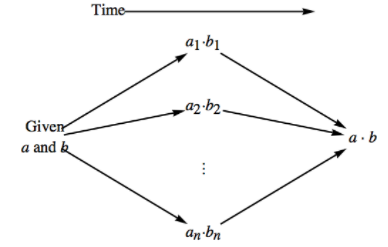Figura\(\PageIndex{1}\): Cálculo concurrente en un producto directo

Nota\(\PageIndex{1}\)

1. Sobre la notación. Si dos o más factores consecutivos en un producto directo son idénticos, es común combinarlos usando notación exponencial. Por ejemplo, se\(\mathbb{Z} \times \mathbb{Z} \times \mathbb{R}\) puede escribir\(\mathbb{Z}^2 \times \mathbb{R}\text{,}\) y se\(\mathbb{R} \times \mathbb{R} \times \mathbb{R} \times \mathbb{R}\) puede escribir\(\mathbb{R}^4\text{.}\) Esto es puramente una conveniencia notacional; no se está produciendo realmente ninguna exponenciación.
2. Llamamos a las operaciones en un producto directo por componentes operaciones, y de hecho son operaciones en\(V\text{.}\) Si dos\(n\) -tuplas,\(a\) y\(b\text{,}\) se seleccionan de\(V\text{,}\) los primeros componentes de\(a\) y\(b\text{,}\)\(a_1\) y\(b_1\text{,}\) son operado con\(*_1\) para obtener\(a_1*_1b_1\text{,}\) el primer componente de\(a * b\text{.}\) Note que ya que\(*_1\) es una operación on\(V_1\text{,}\)\(a_1*_1b_1\) es un elemento de\(V_1\text{.}\) Similarmente, todos los demás componentes de\(a * b\text{,}\) como se definen, pertenecen a sus conjuntos propios.
3. Un hecho significativo sobre las operaciones por componentes es que todos los componentes del resultado se pueden calcular al mismo tiempo (simultáneamente). El tiempo requerido para calcular en un producto directo se puede reducir a un período de tiempo que no sea mucho mayor que la cantidad máxima de tiempo necesario para calcular los factores.
4. Un producto directo de los sistemas algebraicos no siempre es un sistema algebraico del mismo tipo que sus factores. Esto se debe a que ciertos axiomas que son ciertos para los factores pueden no ser ciertos para el conjunto de\(n\) -tuplas. Sin embargo, esta situación no ocurre con los grupos. Encontrarás que siempre que se introduzca un nuevo tipo de sistema algebraico, llámalo tipo\(T\text{,}\) uno de los primeros teoremas que suele probarse, si es posible, es que el producto directo de dos o más sistemas de tipo\(T\) es un sistema de tipo\(T\text{.}\)

Productos Directos de Grupos

Teorema\(\PageIndex{1}\): The Direct Product of Groups is a Group

El producto directo de dos o más grupos es un grupo; es decir, las propiedades algebraicas de un sistema obtenidas tomando el producto directo de dos o más grupos incluye los axiomas del grupo.

Prueba

Sólo presentaremos la prueba de este teorema para el producto directo de dos grupos. Se pueden hacer algunas pequeñas revisiones para producir una prueba de cualquier número de factores.

Afirmar que el producto directo de dos grupos es un grupo es una manera corta de decir que si\(\left[G_1; *_1\right]\) y\(\left[G_2; *_2\right]\) son grupos, entonces también\(\left[G_1\times G_2; * \right]\) es un grupo, donde\(*\) está la operación componentwise sobre\(G_1\times G_2\text{.}\) Asociatividad de\(*\): Si\(a, b, c \in G_1\times G_2\text{,}\)

\ begin {equation*}\ begin {split} a * (b * c) & =\ left (a_1, a_2\ right) *\ left (\ left (b_1, b_2\ right) *\ left (c_1, c_2\ right)\ right)\\ right)\\ & =\ left (a_1, a_2\ right) *\ left (b_1*_1c_1, _2*_2c_2\ derecha)\\ & =\ izquierda (a_1*_1\ izquierda (b_1*_1c_1\ derecha), a_2*_2\ izquierda (b_2*_2c_2\ derecha)\ derecha)\\ & =\ izquierda (\ izquierda (a_1*_1b_1\ derecha) *_1c_ 1,\ izquierda (a_2*_2b_2\ derecha) *_2c_2\ derecha)\\ & =\ izquierda (a_1*_1b_1, a_2*_2b_2\ derecha) *\ izquierda (c_1, c_2\ derecha)\\ & = izquierda (\ izquierda (a_1, a_2\ derecha) *\ izquierda (b_1, b_2\ derecha)\ derecha)\ izquierda (c_1, c_2\ derecha)\\ & = (a * b) *c\\\ final {dividir}\ final {ecuación*}

Observe cómo la propiedad de asociatividad depende de la asociatividad en cada factor. Una identidad para\(*\text{:}\) Como es de esperar, si\(e_1\) y\(e_2\) son identidades para\(G_1\) y\(G_2\text{,}\) respectivamente, entonces\(e = \left(e_1, e _2 \right)\) es la identidad para\(G_1 \times G_2\text{.}\) If\(a \in G_1\times G_2\text{,}\)

\ begin {ecuación*}\ begin {split} a * e &=\ left (a_1, a_2\ right) *\ left (e_1, e _2\ right)\\ & =\ left (a_1*_1e_1, a_2*_2 e _2\ right)\\ & =\ left (a_1, a_2\ right) = a\ end {split}\ end {ecuación*}

Del mismo modo,\(e * a = a\text{.}\)

Invierte en\(G_1\times G_2\text{:}\) La inversa de un elemento se determina componentwise\(a^{-1}= \left(a_1,a_2\right){}^{-1}=\left(a_1{}^{-1},a_2{}^{-1}\right)\text{.}\) Para verificar, calculamos\(a * a^{-1}\):

\ begin {ecuación*}\ begin {split} a * a^ {-1} &=\ izquierda (a_1, a_2\ derecha) *\ izquierda (a_1 {} ^ {-1}, a_2 {} ^ {-1}\ derecha)\\ & =\ izquierda (a_1*_1a_1 {} ^ {-1}, a_2*_2a_2 {} ^ {-1}\ derecha)\\ & =\ izquierda (e_1, e _2\ derecha) =e\ end {split}\ end {ecuación*}

Del mismo modo,\(a^{-1} * a=e\text{.}\)

Ejemplo\(\PageIndex{2}\): Some New Groups

1. Si\(n \geq 2\text{,}\)\(\mathbb{Z}_2{}^n\), el producto directo de\(n\) factores de\(\mathbb{Z}_2\text{,}\) es un grupo con\(2^n\) elementos. Vamos a echar un vistazo más de cerca a\(\mathbb{Z}_2{}^3 = \mathbb{Z}_2 \times \mathbb{Z}_2 \times \mathbb{Z}_2\text{.}\) Los elementos de este grupo son triples de ceros y unos. Dado que la operación en\(\mathbb{Z}_2\) es\(+_2\text{,}\) usaremos el símbolo + para la operación on\(\mathbb{Z}_2{}^3\). Dos de los ocho triples del grupo son\(a = (1, 0, 1)\) y\(b = (0, 0, 1)\text{.}\) Su “suma” es\(a + b = \left(1 +_2 0, 0 +_2 0, 1 +_2 1\right) = (1, 0, 0)\text{.}\) Un dato interesante de este grupo es que cada elemento es su propio inverso. Por ejemplo\(a + a = (1, 0, 1) + (1, 0, 1) = (0, 0, 0)\text{;}\) por lo tanto\(-a = a\text{.}\) Utilizamos la notación aditiva para la inversa de\(a\) porque estamos usando una forma de adición. Tenga en cuenta que\(\{(0, 0, 0), (1, 0, 1)\}\) es un subgrupo de\(\mathbb{Z}_2{}^3\text{.}\) Escriba la tabla de “suma” para este conjunto y aplique el Teorema 11.5.2. Lo mismo puede decirse de cualquier conjunto constituido por (0, 0, 0) y otro elemento de\(\mathbb{Z}_2{}^3\text{.}\)
2. El producto directo de los números reales positivos con los enteros módulo 4,\(\mathbb{R}^+ \times \mathbb{Z}_4\) es un grupo infinito ya que uno de sus factores es infinito. Las operaciones sobre los factores son multiplicación y suma modular, por lo que seleccionaremos el símbolo neutro\(\diamond\) para la operación en\(\mathbb{R}^+ \times \mathbb{Z}_4\text{.}\) If\(a = (4, 3)\) y\(b = (0.5, 2)\text{,}\) luego
   \ begin {equation*}\ begin {array} {c} a\ diamond b = (4, 3)\ diamond (0.5, 2) =\ left (4\ cdot 0.5, 3 +_4 2\ derecha) = (2, 1)\\ b^2 = b\ diamante b = (0.5, 2)\ diamante (0.5, 2) = (0.25, 0)\\ a^ {-1} =\ izquierda (4^ {-1}, -3\ derecha) = (0.25, 1)\ b^ {-1} =\ izquierda (0.5^ {-1}, -2\ derecha) = (2, 2)\ final {array}\ end {equation*}
   Sería incorrecto decir que\(\mathbb{Z}_4\) es un subgrupo de\(\mathbb{R}^+\times \mathbb{Z}_4\), pero hay un subgrupo del producto directo que se asemeja mucho\(\mathbb{Z}_4\text{.}\) es\(\{(1, 0), (1, 1), (1, 2), (1, 3)\}\text{.}\) Su tabla es
   \ begin {ecuation*}\ begin {array} {c|cccc}\ diamond & (1, 0) & (1, 1) & (1, 2) & (1, 3)\\ hline (1, 0) & (1, 0) & (1, 1) & (1, 2) & (1, 2) & (1, 3)\ (1, 1) y (1, 1) y (1, 2) y ; (1, 3) & (1, 0)\\ (1, 2) & (1, 2) & (1, 3) & (1, 0) & (1, 1)\\ (1, 3) & (1, 3) & (1, 0) & (1, 0) & (1, 1) & (1, 2)\\ end {array}\ end {ecuación*}
   Imagine borrar en\((1, )\) toda la tabla y escribir\(+_4\) en lugar de\(\diamond\text{.}\) ¿Qué obtendrías? Exploraremos este fenómeno en detalle en la siguiente sección.
   Todo el producto directo se pudo visualizar como cuatro medias líneas paralelas etiquetadas como 0, 1, 2 y 3 como en la Figura\(\PageIndex{2}\). En la línea\(k\) th, el punto que yace\(x\) unidades a la derecha de la marca cero sería\((x,k)\text{.}\) El conjunto\(\{(2^n, (n)1) \mid n \in \mathbb{Z}\}\text{,}\) que se representa en la figura es un subgrupo de\(\mathbb{R}^+\times \mathbb{Z}_4\text{.}\) ¿Qué subgrupo cíclico es?
   La respuesta:\(\langle (2, 1)\rangle\) o\(\langle(1/2, 3)\rangle\text{.}\) Hay dos generadores diferentes.

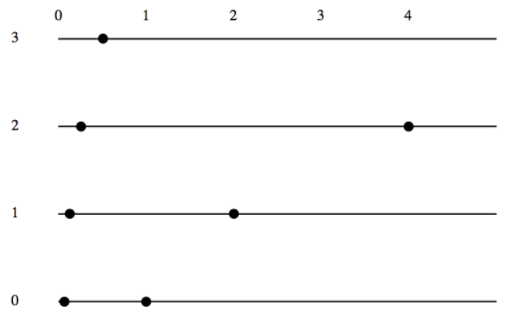Figura\(\PageIndex{2}\): Visualización del grupo\(\mathbb{R}^{+}\times\mathbb{Z}_{4}\)

Un producto directo más convencional es\(\mathbb{R}^2\text{,}\) el producto directo de dos factores de\([\mathbb{R}; + ]\text{.}\) La operación en\(\mathbb{R}^2\) es la adición por componentes; de ahí que usaremos + como símbolo de operación para este grupo. Debe estar familiarizado con esta operación, ya que es idéntica a la adición de\(2 \times 1\) matrices. El sistema de coordenadas cartesianas se puede utilizar para visualizar\(\mathbb{R}^2\) geométricamente. Trazamos el par\((s, t)\) en el plano de la manera habitual:\(s\) unidades a lo largo del\(x\) eje y\(t\) unidades a lo largo del\(y\) eje. Hay una variedad de diferentes subgrupos de\(\mathbb{R}^2\), algunos de los cuales son:

1. \(\{(x, 0) \mid x \in \mathbb{R}\}\text{,}\)todos los puntos en el\(x\) eje;
2. \(\{(x, y) \mid 2x- y = 0\}\text{,}\)todos los puntos que están en la línea 2x - y = 0;
3. Si\(a, b \in \mathbb{R}\text{,}\)\(\{(x, y) \mid a x + b y = 0\}\text{.}\) Los dos primeros subgrupos son casos especiales de éste, que representa cualquier línea que pase por el origen.
4. \(\{(x, y) \mid 2x - y = k, k \in \mathbb{Z}\}\text{,}\)una unión de un conjunto de líneas que son paralelas a\(2x - y = 0\text{.}\)
5. \(\{(n, 3n) \mid n \in \mathbb{Z}\}\text{,}\)que es el único subgrupo contable que hemos enumerado.

Dejaremos al lector verificar que estos conjuntos son subgrupos. Sólo vamos a señalar cómo el cuarto ejemplo, llamarlo\(H\text{,}\) se cierra bajo “suma”. Si\(a = (p, q)\) y\(b = (s, t)\) y ambos pertenecen a\(H\text{,}\) entonces\(2p - q = j\) y\(2s - t= k\text{,}\) donde ambos\(j\) y\(k\) son enteros. \(a + b = (p, q) + (s, t) = (p + s, q + t)\)Podemos determinar si\(a + b\) pertenece a\(H\) decidiendo si\(2(p + s) - (q + t)\) es o no un entero:

\ begin {equation*}\ begin {split} 2 (p + s) - (q + t) &= 2p + 2s - q - t\\ & = (2p - q) + (2s - t)\\ & = j + k\ end {split}\ end {equation*}

Ya que\(j\) y\(k\) son enteros, así es\(j +k\text{.}\) Esto completa una prueba que\(H\) se cierra bajo la operación de\(\mathbb{R}^2\text{.}\)

Se pueden exponer varios hechos útiles en lo que respecta al producto directo de dos o más grupos. Los combinaremos en un teorema, que presentaremos sin pruebas. Las partes a y c se derivaron para\(n = 2\) en la prueba del Teorema\(\PageIndex{1}\).

Teorema\(\PageIndex{2}\): Properties of Direct Products of Groups

Si\(G = G_1\times G_2 \times \cdots \times G_n\) es un producto directo de\(n\) grupos y\(\left(a_1, a_2 , \dots , a_n\right) \in G\text{,}\) luego:

1. La identidad de\(G\) es\(\left(e_1, e_2 , . . . , e_n\right)\text{,}\) donde\(e_k\) está la identidad de\(G_k\text{.}\)
2. \(\left(a_1, a_2 , . . . , a_n\right) {}^{-1}= \left(a_1{}^{-1}, a_2{}^{-1} , . . . , a_n{}^{-1}\right)\text{.}\)
3. \(\left(a_1, a_2 , . . . , a_n\right) {}^m= \left(a_1{}^m, a_2{}^m , . . . , a_n{}^m\right)\)para todos\(m\in \mathbb{Z}\text{.}\)
4. \(G\)es abeliano si y sólo si cada uno de los factores\(G_1, G_2, \ldots , G_n\) es abeliano.
5. Si\(H_1, H_2, \ldots , H_n\) son subgrupos de los factores correspondientes, entonces\(H_1\times H_2 \times \cdots \times H_n\) es un subgrupo de\(G\text{.}\)

No todos los subgrupos de un producto directo pueden ser creados usando la parte e del Teorema\(\PageIndex{2}\). Por ejemplo,\(\{(n, n) \mid n \in \mathbb{Z}\}\) es un subgrupo de\(\mathbb{Z}^2\text{,}\) pero no es un producto directo de dos subgrupos de\(\mathbb{Z}\text{.}\)

Ejemplo\(\PageIndex{3}\): Linked Lists using a Direct Product

Usando la identidad\((x + y) + x = y\text{,}\) en\(\mathbb{Z}_2\text{,}\) podemos idear un esquema para representar una lista enlazada simétricamente usando solo un campo de enlace. Una lista enlazada simétricamente es una lista en la que cada nodo contiene un puntero a su sucesor inmediato y su predecesor inmediato (ver Figura\(\PageIndex{3}\)). Si los punteros son direcciones binarias\(n\) -dígitos, entonces cada puntero se puede tomar como un elemento de\(\mathbb{Z}_2{}^n\text{.}\) Listas de este tipo se puede lograr usando celdas con un solo enlace. En lugar de un puntero izquierdo y uno derecho, el único “enlace” es el valor de la suma (enlace izquierdo) + (enlace derecho). Todas las operaciones de lista estándar (fusionar, insertar, eliminar, poligonal, etc.) son posibles con esta estructura, siempre que conozca el valor del puntero nulo y la dirección,\(f\text{,}\) de la primera celda (es decir, más a la izquierda). Ya que primero\(f.\textrm{ left}\) es nulo, podemos recuperar\(f.\textrm{ right}\) sumando el valor de nulo:\(f + \textrm{ nil} = (\textrm{ nil} + f.\textrm{right}) + \textrm{nil} = f.\textrm{right}\text{,}\) que es la dirección del segundo ítem. Ahora si conservamos temporalmente la dirección,\(s\text{,}\) de la segunda celda, podemos recuperar la dirección del tercer ítem. El campo de enlace del segundo ítem contiene la suma\(s.\textrm{ left} + s.\textrm{ right} = \textrm{ first} + \textrm{ third}\text{.}\) Por lo tanto

\ begin {ecuación*}\ begin {split} (\ textrm {primero} +\ textrm {tercero}) +\ textrm {primero} &= s + s.\ textrm {izquierda}\\ &= (s.\ textrm {izquierda} + s.\ textrm {derecha}) + s.\ textrm {izquierda}\\ textrm {izquierda}\\ &=s.\ textrm {izquierda}\ textrm m {derecha}\\ &=\ textrm {tercero}\ end {split}\ end {ecuación*}

Ya no necesitamos la dirección de la primera celda, sólo la segunda y la tercera, para recuperar la cuarta dirección, y así sucesivamente.

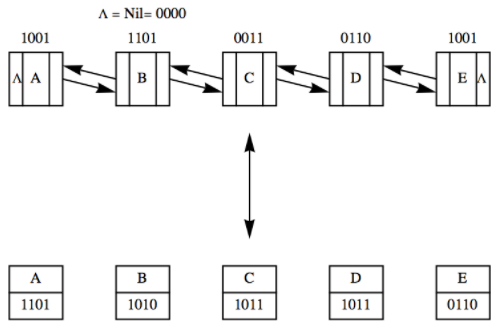Figura\(\PageIndex{3}\): Listas enlazadas simétricas

El siguiente algoritmo más formal utiliza nombres que reflejan el momento de las visitas.

Dada una lista simétrica, se realiza un recorrido de la lista de la siguiente manera, donde\(\textit{first}\) está la dirección de la primera celda. Presumimos que cada ítem tiene alguna información que está representada por\(\textrm{item}.\textrm{info}\) y un campo llamado item.link que es la suma de los enlaces izquierdo y derecho.

Mesa\(\PageIndex{1}\)

(1) ayer =nil

(2) hoy =primero

(3)\(\quad \) mientras\(\textrm{today} \neq \textrm{nil}\text{:}\)

\(\quad \quad \quad \)(3.1) Escribir (today.info)

\(\quad \quad \quad \)(3.2) mañana = hoy.link + ayer

\(\quad \quad \quad \)(3.3) ayer = hoy

\(\quad \quad \quad \)(3.4) hoy = mañana.

En cualquier momento de este algoritmo sería bastante fácil insertar una celda entre hoy y mañana. ¿Puede describir cómo se lograría esto?

Ejercicios

Ejercicio\(\PageIndex{1}\)

Escribe la tabla de grupos de\(\mathbb{Z}_2 \times \mathbb{Z}_3\) y encuentra los dos subgrupos propios de este grupo.

Contestar

Tabla de\(\mathbb{Z}_2\times \mathbb{Z}_3\text{:}\)

\ begin {ecuación*}\ begin {array} {c|cccccc} +& (0,0) & (0,1) & (0,2) & (1,0) & (1,1) & (1,2)\\ hline (0,0) & (0,0) & (0,1) & (0,2) & (1,0) & (1,1) & (1,1) & (1,2)\\ (0,1) & (0,1) & (0,2) & (0,0) y (1,1) y (1,2) y (1,0)\\ (0,2) y (0,2) y (0,0) y (0,1) y (1,2) y (1,0) y (1,1) \\ (1,0) y (1,0) & (1,1) & (1,2) & (0,0) & (0,1) & (0,2)\\ (1,1) & (1,1) & (1,2) & (1,0) & (1,0) & (0,1) & (0,2) & (0,0)\ (1,2) & (1,2) & (1,0) & (1,1) & (0,2) & (0,0) & (0,1)\ end array {}\ end {ecuación*}

Los dos únicos subgrupos propios son\(\{(0, 0), (1, 0)\}\) y\(\{(0, 0), (0, 1), (0, 2)\}\)

Ejercicio\(\PageIndex{2}\)

Enumere más ejemplos de subgrupos propios de los\(\mathbb{R}^2\) que son diferentes a los enumerados en esta sección.

Ejercicio\(\PageIndex{3}\): Algebraic Properties of the \(n\)-Cube

1. Los cuatro elementos de se\(\mathbb{Z}_2{}^2\) pueden visualizar geométricamente como las cuatro esquinas del 2-cube. Describir algebraicamente los enunciados:
   1. Esquinas\(a\) y\(b\) son adyacentes.
   2. Esquinas\(a\) y\(b\) están diagonalmente opuestas entre sí.
2. Los ocho elementos de se\(\mathbb{Z}_2{}^3\) pueden visualizar como las ocho esquinas del cubo 3. Una cara contiene\(\mathbb{Z}_2 \times \mathbb{Z}_2\times \{0\}\) y la cara opuesta contiene los cuatro elementos restantes por lo que\((a, b, 1)\) está detrás\((a, b, 0)\text{.}\) Como en la parte a, describir las declaraciones i y ii algebraicamente.
3. Si pudieras imaginar una figura geométrica similar al cuadrado o cubo en\(n\) dimensiones, y sus esquinas fueran etiquetadas por elementos de\(\mathbb{Z}_2{}^n\) como en las partes a y b, ¿cómo se expresarían algebraicamente las declaraciones i y ii?

Contestar

1. i\(a + b \textrm{ could be }(1, 0) \textrm{ or } (0, 1)\text{.}\)) ii\(a + b = (1, 1)\text{.}\)
2. i\(a + b \textrm{ could be}(1, 0, 0), (0, 1, 0), \textrm{ or }(0, 0, 1)\text{.}\)) ii\(a + b = (1, 1, 1)\text{.}\)
3. (i)\(a + b\) tiene exactamente uno 1. (ii)\(a + b\) tiene todos\(1's\text{.}\)

Ejercicio\(\PageIndex{4}\)

1. Supongamos que te iban a dar un grupo\([G; * ]\) y te pidieran resolver la ecuación\(x * x = e\text{.}\) Sin conocer el grupo, ¿puedes anticipar cuántas soluciones habrá?
2. Responde la misma pregunta como parte a para la ecuación\(x * x = x\text{.}\)

Ejercicio\(\PageIndex{5}\)

¿Cuáles de los siguientes conjuntos son subgrupos de\(\mathbb{Z} \times \mathbb{Z}\text{?}\) Dar una razón para cualquier respuesta negativa?

1. \(\displaystyle \{0\}\)
2. \(\displaystyle \{(2j, 2k) \mid j,k\in \mathbb{Z}\}\)
3. \(\displaystyle \{(2j+ 1, 2k) \mid j,k\in \mathbb{Z}\}\)
4. \(\displaystyle \{(n, n^2 ) \mid n \in \mathbb{Z}\}\)
5. \(\displaystyle \{(j, k) \mid j + k\textrm{ is} \textrm{ even}\}\)

Contestar

1. No, 0 no es un elemento de\(\mathbb{Z} \times \mathbb{Z}\text{.}\)
2. Sí.
3. No, no\((0, 0)\) es un elemento de este conjunto.
4. No, el conjunto no está cerrado:\((1, 1) + (2, 4) = (3, 5)\) y no\((3, 5)\) está en el conjunto.
5. Sí.

Ejercicio\(\PageIndex{6}\)

Determinar los siguientes valores en el grupo\(\mathbb{Z}_3 \times \mathbb{R}^*\text{:}\)

1. \(\displaystyle (2,1)* (1,2)\)
2. el elemento de identidad
3. \(\displaystyle (1, 1/2)^{-1}\)