11.7: Isomorfismos

Última actualización
Guardar como PDF

Page ID: 117334

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Se debe memorizar la siguiente definición informal de sistemas isomórficos. No importa cuán técnica sea una discusión sobre los sistemas isomórficos, hay que tener en cuenta que esta es la esencia del concepto.

Definición$\PageIndex{1}$: Isomorphic Systems/Isomorphism - Informal

Dos sistemas algebraicos son isomórficos si existe una regla de traducción entre ellos para que cualquier declaración verdadera en un sistema pueda traducirse en una declaración verdadera en el otro.

Ejemplo$\PageIndex{1}$: How to Do Greek Arithmetic

Imagina que eres un niño de seis años que ha sido criado en una familia de habla inglesa, se ha mudado a Grecia y se ha matriculado en una escuela griega. Supongamos que su nuevo maestro le pide a la clase que haga el siguiente problema de adición que ha sido escrito en griego.

\ begin {ecuación*}\ tau\ rho\ aguda {\ iota}\ alfa\ quad\ sigma\ upsilon\ nu\ quad\ tau\ aguda {\ épsilon}\ sigma\ sigma\ varepsilon\ rho\ alfa\ quad\ iota\ sigma o\ aguda {\ upsilon}\ tau\ alfa\ iota\ quad\ _\ _\ _\ fin ecuación*}

Lo natural que puedes hacer es sacar tu diccionario griego-inglés/inglés-griego y traducir las palabras griegas al inglés, como se describe en Figura$\PageIndex{1}$ Una vez que hayas resuelto el problema, puedes consultar el mismo diccionario para encontrar la palabra griega adecuada que el profesor quiera. Si bien este no es el método recomendado para aprender una lengua extranjera, seguramente dará la respuesta correcta al problema. Matemáticamente, podemos decir que el sistema de enteros griegos con suma ($\sigma \upsilon \nu$) es isomórfico a enteros ingleses con suma (más). Sin embargo, el problema de la traducción entre lenguas naturales es más difícil que esto, porque dos lenguajes naturales completos no son isomórficos, o al menos el isomorfismo entre ellos no está contenido en un diccionario simple.

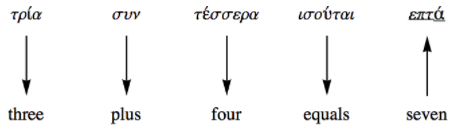$clipboard_e2cd2540e870adf7ec3feef038434a533.png$ Figura$\PageIndex{1}$: Solución de un problema aritmético griego

Ejemplo$\PageIndex{2}$: Software Implementation of Sets

En este ejemplo, describiremos cómo se pueden implementar las variables establecidas en una computadora. Primero describiremos los dos sistemas y luego describiremos el isomorfismo entre ellos.

Sistema 1: El conjunto de potencia de$\{1, 2, 3, 4, 5\}$ con la unión de operación,$\cup\text{.}$ Por simplicidad, solo discutiremos unión. Sin embargo, las otras operaciones se implementan de manera similar.

Sistema 2: Cadenas de cinco bits de memoria de computadora con puerta OR. Los valores de bit individuales son cero o uno, por lo que los elementos de este sistema pueden visualizarse como secuencias de cinco 0 y 1. Una puerta OR, Figura$\PageIndex{2}$, es una pequeña pieza de hardware de computadora que acepta dos valores de bit en cualquier momento y genera un cero o uno, dependiendo de las entradas. La salida de una puerta OR es una, excepto cuando los dos valores de bit que acepta son ambos cero, en cuyo caso la salida es cero. La operación en este sistema consiste en introducir secuencialmente los valores de dos cadenas de bits en la puerta OR. El resultado será una nueva cadena de cinco 0 y 1. Un método alternativo para operar en este sistema es usar cinco puertas OR e ingresar pares de bits correspondientes de las cadenas de entrada a las puertas simultáneamente.

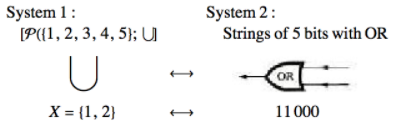$clipboard_e14dd3c2b80de7e05eddcbffed880c909.png$ Figura$\PageIndex{2}$: Traducción entre conjuntos y cadenas de bits

El isomorfismo: Dado que cada sistema tiene una sola operación, es evidente que la unión y la puerta OR se traducen entre sí. La traducción entre conjuntos y cadenas de bits es más fácil de describir mostrando cómo construir un conjunto a partir de una cadena de bits. Si$a_1a_2a_3a_4a_5\text{,}$ es una cadena de bits en el Sistema 2, el conjunto al que se traduce contiene el número$k$ si y solo si$a_k$ es igual a 1. Por ejemplo,$10001$ se traduce al conjunto$\{1, 5\}\text{,}$ mientras que el conjunto$\{1, 2\}$ se traduce a$11000.$ Ahora imagina que tu computadora es como el niño que sabe inglés y debe hacer un problema griego. Para ejecutar un programa que tenga código que incluya la expresión set seguirá el mismo procedimiento$\{1, 2\} \cup \{1, 5\}\text{,}$ que el hijo para obtener el resultado, como se muestra en la Figura$\PageIndex{3}$.

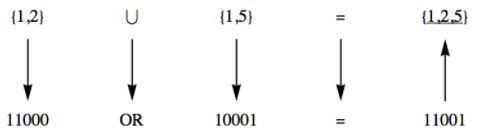$clipboard_e2a60a39d287e2b93f29b7e71ac8ce5ac.png$ Figura$\PageIndex{3}$: Traducción de un problema en teoría de conjuntos

Isomorfismos grupales

Ejemplo$\PageIndex{3}$: Multiplying Without Doing Multiplication

Este isomorfismo es entre$\left[\mathbb{R}^+ ; \cdot \right]$ y$[\mathbb{R};+]\text{.}$ Hasta la década de 1970, cuando bajó el precio de las calculadoras, se realizaron multiplicación y exponenciación con un isomorfismo entre estos sistemas. El isomorfismo$\left(\mathbb{R}^+\right.$ a$\mathbb{R}$) entre los dos grupos$\cdot$ es que se traduce en$+$ y cualquier número real positivo$a$ se traduce al logaritmo de$a\text{.}$ Para traducir de vuelta de$\mathbb{R}$ a$\mathbb{R}^+$, se invierte la función logaritmo. Si se utilizan logaritmos base diez, un elemento de$\mathbb{R}\text{,}$$b\text{,}$ se traducirá a$10^b\text{.}$ En días previos a la calculadora, la traducción se realizó con una tabla de logaritmos o con una regla de cálculo. Un ejemplo de cómo se utiliza el isomorfismo aparece en la Figura$\PageIndex{4}$.

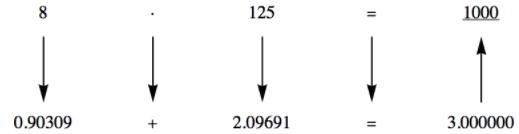$clipboard_e9ed2f6003029ac191e16fde41e1587d7.png$ Figura$\PageIndex{4}$: Multiplicación usando logaritmos

La siguiente definición de isomorfismo entre dos grupos es una definición más formal que aparece en la mayoría de los textos de álgebra abstracta. A primera vista, parece diferente, es realmente una ligera variación de la definición informal. Es la definición común porque es fácil de aplicar; es decir, dada una función, esta definición te dice qué hacer para determinar si esa función es un isomorfismo.

Definición $\PageIndex{2}$: Group Isomorphism

Si$\left[G_1 ; *_1\right]$ y$\left[G_2 ; *_2\right]$ son grupos,$f: G_1 \to G_2$ es un isomorfismo de$G_1$ dentro$G_2$ si:

$f$es una biyección, y
$f\left(a *_1 b\right) = f(a) *_2f(b)$para todos$a, b\in G_1$

Si tal función existe, entonces decimos que$G_1$ es isomórfica para$G_2\text{,}$ denotar$G_1 \cong G_2\text{.}$

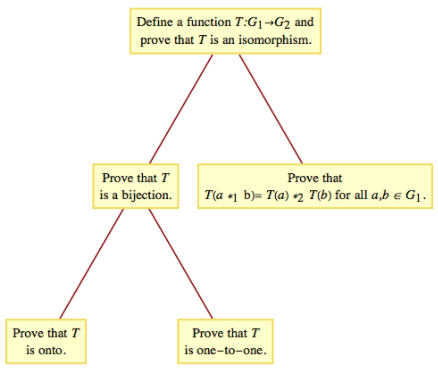$clipboard_ea3dc7ac49953b62105e94cd25f077404.png$ Figura$\PageIndex{5}$: Pasos para probar eso$G_{1}$ y$G_{2}$ son isomórficos

Nota$\PageIndex{1}$

Podría haber varios isomorfismos diferentes entre el mismo par de grupos. Así, si se le pide demostrar que dos grupos son isomórficos, su respuesta no necesita ser única.
Cualquier aplicación de esta definición requiere de un procedimiento esbozado en la Figura$\PageIndex{5}$. La primera condición, que un isomorfismo sea una biyección, refleja el hecho de que toda afirmación verdadera en el primer grupo debe tener exactamente una declaración verdadera correspondiente en el segundo grupo. Esta es exactamente la razón por la que nos encontramos con dificultades para traducir entre dos lenguajes naturales. Para ver cómo la Condición (b) de la definición formal es congruente con la definición informal, considere la función$L:\mathbb{R}^+\to \mathbb{R}$ definida por$L(x) = \log _{10}x\text{.}$ El diagrama de traducción entre$\mathbb{R}^+$ y$\mathbb{R}$ para el problema de multiplicación$a \cdot b$ aparece en la Figura$\PageIndex{6}$. Llegamos al mismo resultado calculando$L^{-1} (L(a) + L(b))$ como lo hacemos calculando$a \cdot b\text{.}$ Si aplicamos la función$L$ a los dos resultados, obtenemos la misma imagen:
\[\label{eq:1}L(a\cdot b)=L(L^{-1}(L(a)+L(b)))=L(a)+L(b)\]
ya$L\left(L^{-1}(x)\right) = x\text{.}$ Note que$\eqref{eq:1}$ es exactamente Condición b de la definición formal aplicado a los dos grupos$\mathbb{R}^+$ y$\mathbb{R}\text{.}$

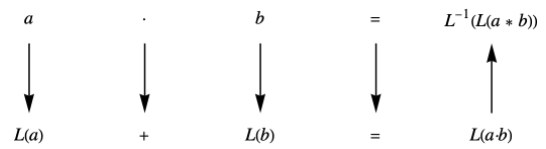$clipboard_e4113a689550d395ccd4b639c1e7c5af0.png$ Figura$\PageIndex{6}$: Multiplicación general usando logaritmos

Ejemplo$\PageIndex{4}$

Considerar$G= \left\{\left.\left( \begin{array}{cc} 1 & a \\ 0 & 1 \\ \end{array} \right) \right| a \in \mathbb{R}\right\}$ con multiplicación matricial. El grupo$[\mathbb{R};+]$ es isomórfico a$G\text{.}$ Nuestra regla de traducción es la función$f: \mathbb{R} \to G$ definida por$f(a)=\left( \begin{array}{cc} 1 & a \\ 0 & 1 \\ \end{array} \right)\text{.}$ Dado que los grupos tienen una sola operación, no hay necesidad de afirmar explícitamente que la suma se traduce a la multiplicación matricial. Eso$f$ es una bijección queda claro a partir de su definición.

Si$a$ y$b$ son números reales,

\ begin {ecuación*}\ begin {split} f (a) f (b) & =\ left (\ begin {array} {cc} 1 & a\\ 0 & 1\\\ end {array}\ right)\ left (\ begin {array} {cc} 1 & b\\ 0 & 1\\ end {array}\ right)\\ & =\ left (\ begin {array} {cc {} 1 & a + b\\ 0 & 1\\\ end {array}\ derecha)\\ & = f (a + b)\ end {split}\ end { ecuación*}

Podemos aplicar esta regla de traducción para determinar la inversa de una matriz en$G\text{.}$ Sabemos que$a + (-a)=0$ es una declaración verdadera en$\mathbb{R}\text{.}$ Using$f$ to translate this statement, we get

\ begin {ecuación*} f (a) f (-a) = f (0)\ end {ecuación*}

\ begin {ecuation*}\ left (\ begin {array} {cc} 1 & a\\ 0 & 1\\\ end {array}\ right)\ left (\ begin {array} {cc} 1 & -a\\ 0 & 1\\\ end {array}\ right) =\ left (\ begin {array} {cc} 1 & 0\\ 0 & 1\\\ end {array} derecha)\ end {ecuación*}

por lo tanto,

\ begin {ecuación*}\ left (\ begin {array} {cc} 1 & a\\ 0 & 1\\\ end {array}\ right) ^ {-1} =\ left (\ begin {array} {cc} 1 & -a\\ 0 & 1\\\ end {array}\ derecha)\ end {ecuación*}

El siguiente teorema resume algunos de los hechos generales sobre los isomorfismos grupales que se utilizan con mayor frecuencia en las aplicaciones. Dejamos la prueba al lector.

Teorema$\PageIndex{1}$: Properties of Isomorphisms

Si$[G;*]$ y$[H;\diamond ]$ son grupos con identidades$e$ y$e'\text{,}$ respectivamente, y$T:G \to H$ es un isomorfismo desde$G$$H\text{,}$ entonces:

$\displaystyle T(e) = e'$
$T(a)^{-1} = T\left(a^{-1}\right)$para todos$a \in G\text{,}$ y
Si$K$ es un subgrupo de$G\text{,}$ entonces$T(K) = \{T(a) : a \in K\}$ es un subgrupo de$H$ y es isomorfo a$K\text{.}$

“Es isomórfico a” es una relación de equivalencia en el conjunto de todos los grupos. Por lo tanto, el conjunto de todos los grupos se divide en clases de equivalencia, conteniendo cada clase de equivalencia grupos que son isomórficos entre sí.

Condiciones para que los grupos no sean isomórficos

¿Cómo decides que dos grupos no son isomórficos entre sí? La negación de “$G$y$H$ son isomórficos” es que ninguna regla de traducción entre$G$ y$H$ existe. Si$G$ y$H$ tienen diferentes cardinalidades, entonces no$H$ puede existir ninguna biyección de$G$ hacia dentro. De ahí que no sean isomórficos. Dado que generalmente$\left| G\right| =\left| H\right|\text{,}$ no es práctico enumerar todas las bijecciones de$G$ hacia$H$ y mostrar que ninguna de ellas satisface la Condición b de la definición formal. La mejor manera de demostrar que dos grupos no son isomórficos es encontrar una verdadera afirmación sobre un grupo que no sea cierta sobre el otro grupo. Ilustramos este método en la siguiente lista de verificación que puedes aplicar a la mayoría de pares de grupos no isomórficos en este libro.

Supongamos que$[G;*]$ y$[H;\diamond ]$ son grupos. Las siguientes son razones para$G$ y$H$ para no ser isomórfico.

$G$y$H$ no tienen la misma cardinalidad. Por ejemplo, no$\mathbb{Z}_{12} \times \mathbb{Z}_5$ puede ser isomorfo a$\mathbb{Z}_{50}$ y no$[\mathbb{R};+]$ puede ser isomorfo a$\left[\mathbb{Q}^+ ; \cdot \right]\text{.}$
$G$es abeliano y no$H$ es abeliano ya que siempre$a * b = b * a$ es cierto en$G\text{,}$ pero no siempre$T(a) \diamond T(b) = T(b) \diamond T(a)$ sería cierto. Hemos visto dos grupos con seis elementos que aquí aplican. Son$\mathbb{Z}_6$ y el grupo de matrices$3 \times 3$ de gradas (ver Ejercicio 11.2.5). El segundo grupo es no abeliano, por lo tanto no puede ser isomórfico para$\mathbb{Z}_6\text{.}$
$G$tiene cierto tipo de subgrupo que$H$ no tiene. La parte (c) del Teorema$\PageIndex{1}$ afirma que esto no puede suceder si$G$ es isomórfico a$H\text{.}$$\left[\mathbb{R}^* ; \cdot \right]$ y no$\left[\mathbb{R}^+ ; \cdot \right]$ son isomórficos ya que$\mathbb{R}^*$ tiene un subgrupo con dos elementos,$\{-1, 1\}\text{,}$ mientras que los subgrupos propios de$\mathbb{R}^+$ son todos infinitos (¡convencete de este hecho!).
El número de soluciones de$x * x = e$ in no$G$ es igual al número de soluciones de$y \diamond y = e'$ in no$H\text{.}$$\mathbb{Z}_8$ es isomórfico a$\mathbb{Z}_2{}^3$ puesto que$x +_8 x = 0$ tiene dos soluciones, 0 y 4, mientras que$y + y = (0, 0, 0)$ es cierto para todos$y\in \mathbb{Z}_2{}^3\text{.}$ Si la operación en$G$ está definida por un tabla, entonces el número de soluciones de$x * x = e$ será el número de ocurrencias de$e$ en la diagonal principal de la tabla. Las ecuaciones también se$x^3 = e\text{,}$$x^4= e, \dots$ pueden utilizar de la misma manera para identificar pares de grupos no isomórficos.
Uno de los subgrupos cíclicos de$G$ iguales$G$ ($G$es decir, es cíclico), mientras que ninguno$H$ de los subgrupos cíclicos es igual$H$ ($H$es decir, es no cíclico). Este es un caso especial de la Condición c.$\mathbb{Z}$ y no$\mathbb{Z} \times \mathbb{Z}$ son isomórficos ya que$\mathbb{Z} = \langle 1\rangle$ y no$\mathbb{Z} \times \mathbb{Z}$ es cíclico.

Ejercicios

Ejercicio$\PageIndex{1}$

Declarar si cada par de grupos a continuación es isomórfico. Por cada par es decir, dale un isomorfismo; para los que no lo son, da tu razón.

$\mathbb{Z} \times \mathbb{R}$y$\mathbb{R} \times \mathbb{Z}$
$\mathbb{Z}_2\times \mathbb{Z}$y$\mathbb{Z} \times \mathbb{Z}$
$\mathbb{R}$y$\mathbb{Q} \times \mathbb{Q}$
$\mathcal{P}(\{1, 2\})$con diferencia simétrica y$\mathbb{Z}_2{}^2$
$\mathbb{Z}_2{}^2$y$\mathbb{Z}_4$
$\mathbb{R}^4$y$M_{2\times 2}(\mathbb{R})$ con adición de matriz
$\mathbb{R}^2$y$\mathbb{R} \times \mathbb{R}^+$
$\mathbb{Z}_2$y las matrices$2 \times 2$ de la grada
$\mathbb{Z}_6$y$\mathbb{Z}_2\times \mathbb{Z}_3$

Responder

Sí,$f(n, x) = (x, n)$ porque$(n, x) \in \mathbb{Z} \times \mathbb{R}$ es un isomorfismo.
No,$\mathbb{Z}_2\times \mathbb{Z}$ tiene un subgrupo de dos elementos mientras que$\mathbb{Z} \times \mathbb{Z}$ no.
No. $\mathbb{Q} \times \mathbb{Q}$es contable y no$\mathbb{R}$ lo es. Por lo tanto, no puede existir ninguna bijección entre ellos.
Sí.
No.
Sí, un isomorfismo se define por$f\left(a_1, a_2,a_3,a_4\right)=\left( \begin{array}{cc} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} \right)\text{.}$
Sí, un isomorfismo se define por$f\left(a_1,a_2\right)=\left(a_1,10^{a_2}\right)\text{.}$
Sí.
Sí$f(k) = k(1,1)\text{.}$

Ejercicio$\PageIndex{2}$

Si conoces dos lenguajes naturales, demuestra que no son isomórficos.

Ejercicio$\PageIndex{3}$

Demostrar que la relación “es isomórfica con” en grupos es transitiva.

Responder

Considerar tres grupos$G_1\text{,}$$G_2\text{,}$ y$G_3$ con operaciones$*, \diamond , \textrm{ and } \star \text{,}$ respectivamente. Queremos demostrar que si$G_1$ es isomorfo a$G_2\text{,}$ y si$G_2$ es isomorfo a$G_3$, entonces$G_1$ es isomorfo a$G_3\text{.}$

\ begin {ecuación*} G_1\ textrm {isomórfico}\ textrm {a} G_2\ Rightarrow\ textrm {there}\ textrm {existe}\ textrm {an}\ textrm {isomorfismo} f:G_1\ a G_2\ end {ecuación*}

\ begin {ecuación*} G_2\ textrm {isomórfico}\ textrm {a} G_3\ Rightarrow\ textrm {there}\ textrm {existe}\ textrm {an}\ textrm {isomorfismo} G:G_2\ a G_3\ end {ecuación*}

Si componemos$g$ con$f\text{,}$ obtenemos la función$g\circ f:G_1\to G_3\text{,}$ Por Teorema 7.3.2 y Teorema 7.3.3,$g\circ f$ es una biyección, y si$a,b\in G_1\text{,}$

\ begin {ecuación*}\ begin {split} (g\ circ f) (a*b) &=g (f (a*b))\\ &=g (f (a)\ diamante f (b))\ quad\ textrm {desde} f\ textrm {es un isomorfismo}\\ & =g (f (a))\ estrella g (f (b)\ quad\ textrm {desde} g\ textrm {es un isomorfismo}\\ & = (g\ circ f) (a)\ star (g\ circ f) (b)\ end {split}\ end {ecuación*}

Por lo tanto,$g\circ f$ es un isomorfismo desde hasta$G_1$$G_3\text{,}$ demostrar que “es isomórfico a” es transitivo.

Ejercicio$\PageIndex{4}$

Escriba la tabla de operaciones para$G = [\{1, -1, i, -i \}; \cdot ]$ dónde$i$ está el número complejo para el cual$i^2 = - 1\text{.}$ Mostrar que$G$ es isomórfico a$\left[\mathbb{Z}_4;+_4\right]\text{.}$
Resuelva$x^2= -1$ primero traduciendo la ecuación a$\mathbb{Z}_4$, resolviendo la ecuación$\mathbb{Z}_4\text{,}$ y luego traduciendo de nuevo a$G$$G\text{.}$

Ejercicio$\PageIndex{5}$

Los dos grupos$\left[\mathbb{Z}_4;+_4\right]$ y$\left[U_5;\times _5\right]$ son isomórficos. Un isomorfismo$T:\mathbb{Z}_4\to U_5$ se define parcialmente por$T(1)=3\text{.}$ Determinar los valores de$T(0)\text{,}$$T(2)\text{,}$ y$T(3)\text{.}$

Responder: Por Teorema$\PageIndex{1}$ (a),$T(0)$ debe ser 1. $T(2)=T(1+_4 1)=T(1)\times_5 T(1) = 3 \times_5 3 = 4\text{.}$Dado que$T$ es una biyección,$T(3)=2\text{.}$

Ejercicio$\PageIndex{6}$

Demostrar teorema$\PageIndex{1}$.

Ejercicio$\PageIndex{7}$

Demostrar que todos los grupos cíclicos infinitos son isomórficos a$\mathbb{Z}\text{.}$

Responder

Dejar$G$ ser un grupo cíclico infinito generado por$a\text{.}$ Entonces, usando notación multiplicativa,$G=\left\{\left.a^n\right| n\in \mathbb{Z}\right\}\text{.}$ El mapa$T: G \rightarrow \mathbb{Z}$ definido por$T\left(a^n\right)=n$ es un isomorfismo. Esto es efectivamente una función, ya que$a^n=a^m$ implica$n =m\text{.}$ De lo contrario,$a$ tendría un orden finito y no generaría$G\text{.}$

$T$es uno a uno, ya que$T\left(a^n\right) = T\left(a^m\right)$ implica$n = m\text{,}$ así$a^n= a^m\text{.}$
$T$está encendido, ya que para cualquier$n\in \mathbb{Z}\text{,}$$T\left(a^n\right) = n\text{.}$
$\displaystyle T\left(a^n*a^m \right) = T\left(a^{n+m}\right) =n + m\ =T\left(a^n\right)+T\left(a^m\right)$

Ejercicio$\PageIndex{8}$

Demostrar que$\mathbb{R}^*$ es isomórfico para$\mathbb{Z}_2 \times \mathbb{R}\text{.}$
Describa cómo se puede lograr la multiplicación de números reales distintos de cero haciendo solo adiciones y traducciones.

Ejercicio$\PageIndex{9}$

Demostrar que si$G$ es algún grupo y$g$ es algún elemento fijo de$G\text{,}$ entonces la función$\phi _g$ definida por$\phi_g(x) = g*x*g^{-1}$ es un isomorfismo desde$G$ dentro de sí mismo. Un isomorfismo de este tipo se llama automorfismo interno.

Ejercicio$\PageIndex{10}$

Se puede demostrar que existen cinco grupos no isomórficos de orden ocho. Deberías poder describir al menos tres de ellos. Hazlo sin el uso de mesas. Asegúrese de explicar por qué no son isomórficos.

Responder: $\mathbb{Z}_{8}$,$\mathbb{Z}_{2}\times\mathbb{Z}_{4}$, y$\mathbb{Z}_{2}^{3}$. Otro es el cuarto grupo diedro, introducido en la Sección 15.3.