15.3: Grupos de Permutación

Última actualización
Guardar como PDF

Page ID: 117160

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Grupos simétricos

A riesgo de desconcertar la mente del lector, examinaremos ahora grupos cuyos elementos son funciones. Recordemos que una permutación en un conjunto$A$ es una bijección de$A$ hacia$A\text{.}$ Supongamos que$A = \{1, 2, 3\}\text{.}$ hay$3! = 6$ diferentes permutaciones en$A\text{.}$ Llamaremos al conjunto de las 6 permutaciones$S_3\text{.}$ Se enumeran en la siguiente tabla. La forma de matriz para describir una función en un conjunto finito es listar el dominio a través de la fila superior y la imagen de cada elemento directamente debajo de él. Por ejemplo$r_1(1) = 2\text{.}$

Tabla $\PageIndex{1}$: Elementos de$S_{3}$

$i =\left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \\ \end{array} \right)$	$r_1=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 3 & 1 \\ \end{array} \right)$	$r_2=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 1 & 2 \\ \end{array} \right)$
$f_1=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 3 & 2 \\ \end{array} \right) $	$f_2=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \\ \end{array} \right)$	$f_3=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 1 & 3 \\ \end{array} \right)$

La operación que dará$\left\{i,r_1,r_2,f_1,f_2,f_3\right\}$ una estructura de grupo es la composición de funciones. Considera el “producto”$r_1\circ f_3\text{:}$

\ begin {ecuación*}\ begin {array} {c} r_1\ circ f_3 (1) =r_1\ left (f_3 (1)\ right) = r_1 (2) =3\ r_1\ circ f_3 (2) =r_1\ left (f_3 (2)\ right) = r_1 (1) = 2\ _1\ circ f_3 (3) =r_1\ izquierda (f_3 (3)\ derecha) = r_1 (3) = 1\\ end {array}\ text {.} \ end {ecuación*}

Las imágenes de 1, 2 y 3 debajo$r_1\circ f_3$ y$f_2$ son idénticas. Así, por la definición de igualdad para las funciones, podemos decir$r_1\circ f_3=f_2$. La tabla completa para la operación de composición de funciones se da en la Tabla$\PageIndex{2}$.

Mesa$\PageIndex{2}$: Mesa de operaciones para$S_{3}$

$\begin{array}{c|cccccc} \circ & i &r_1 & r_2 & f_1 & f_2 & f_3 \\ \hline i & i &r_1 & r_2 & f_1 & f_2 & f_3 \\ r_1 & r_1 &r_2 & i & f_3 & f_1 & f_2 \\ r_2 & r_2 &i & r_1 & f_2 & f_3 & f_1 \\ f_1 & f_1 & f_2 & f_3 & i & r_1 & r_2 \\ f_2 & f_2 &f_3 & f_1 & r_2 & i & r_1 \\ f_3 & f_3 & f_1 & f_2 & r_1 & r_2 & i \\ \end{array}$

Lista$\PageIndex{1}$

Ni siquiera necesitamos la mesa para verificar que tenemos un grupo. Con base en las siguientes observaciones, el conjunto de todas las permutaciones en cualquier conjunto finito será un grupo.

La composición de la función es siempre asociativa.
La identidad para el grupo es$i\text{.}$ Si$g$ es alguna de las permutaciones on$A$ y$x\in A\text{,}$
\ begin {ecuation*}\ begin {array} {lr} (g\ circ i) (x) = g (i (x)) = g (x)) = g (x) & (i\ circ g) (x) = i (g (x)) = g (x)\\ end {array}\ end {ecuación*}
Por lo tanto$g\circ i = i\circ g=g\text{.}$
Una permutación, por definición, es una biyección. En el Capítulo 7 probamos que esto implica que debe tener una inversa y la inversa misma es una biyección y por ende una permutación. De ahí que todos los elementos de$S_3$ tengan una inversa en$S_3\text{.}$ Si una permutación se muestra en forma de matriz, su inversa se puede obtener intercambiando las dos filas y reordenando las columnas para que la fila superior esté en orden. El primer paso es realmente suficiente para obtener la inversa, pero la clasificación de la fila superior facilita el reconocimiento de la inversa.
Por ejemplo, consideremos una permutación típica en$\{1,2,3,4,5\}\text{,}$$f= \left( \begin{array}{ccccc} 1 & 2 & 3 & 4 & 5 \\ 5 & 3 & 2 & 1 & 4 \\ \end{array} \right)\text{.}$
\ begin {ecuation*} f^ {-1} =\ left (\ begin {array} {ccccc} 5 & 3 & 2 & 1 & 4\\ 1 & 2 & 3 & 4 & 5\\ end {array}\ right) =\ left (\ begin {array} {ccccc} {ccccc} 1 & 2 & 3 & amp; 4 & 5\\ 4 & 3 & 2 & 5 & 1\\\ end {array}\ derecha)\ text {.} \ end {ecuación*}

Nota$\PageIndex{1}$

De Table$\PageIndex{2}$, podemos ver que no$S_3$ es abeliano. Recuerda, no abeliano es la negación de abeliano. La existencia de dos elementos que no conmutan es suficiente para que un grupo no sea abeliano. En este grupo,$r_1$ y$f_3$ es uno de esos pares:$r_1\circ f_3= f_2$ mientras$f_3\circ r_1= f_1\text{,}$ que así$r_1\circ f_3\neq f_3\circ r_1\text{.}$ Precaución: No tomes esto para significar que cada par de elementos tiene que tener esta propiedad. Hay varios pares de elementos en los$S_3$ que se desplazan. De hecho, la identidad,$i\text{,}$ debe desplazarse con todo. También cada elemento debe conmutar con su inversa.

Definición $\PageIndex{1}$: Symmetric Group

Dejar$A$ ser un conjunto no vacío. El conjunto de todas las permutaciones$A$ con la operación de composición de funciones se llama el grupo simétrico en$A\text{,}$ denotado$S_A\text{.}$

La cardinalidad de un conjunto finito$A$ es más significativa que los elementos, y denotaremos por$S_n$ el grupo simétrico en cualquier conjunto de cardinalidad$n\text{,}$$n\geq 1\text{.}$

Ejemplo$\PageIndex{1}$: The Significance of $S_3$

Nuestro ejemplo de apertura,$S_3\text{,}$ es el grupo no abeliano más pequeño. Por esa razón, todos sus propios subgrupos son abelianos: de hecho, todos son cíclicos. La figura$\PageIndex{1}$ muestra el diagrama de Hasse para los subgrupos de$S_3\text{.}$

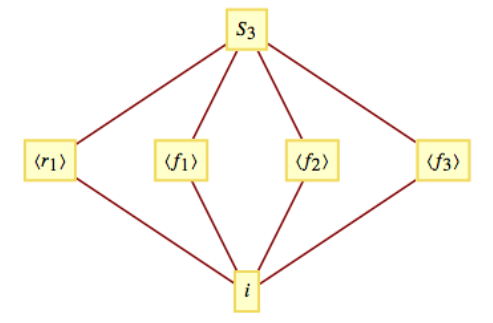$clipboard_e6af63a63397c1e187f3bf49d5a2cce05.png$ Figura$\PageIndex{1}$: Diagrama reticular de subgrupos de$S_3$

Ejemplo$\PageIndex{2}$: Smallest Symmetric Groups

Los únicos grupos simétricos abelianos son$S_1$ y$S_2$, con 1 y 2 elementos, respectivamente. Los elementos de$S_2$ son$i = \left( \begin{array}{cc} 1 & 2 \\ 1 & 2 \\ \end{array} \right)$ y$\alpha = \left( \begin{array}{cc} 1 & 2 \\ 2 & 1 \\ \end{array} \right)\text{.}$$S_2$ es isomórfico a$\mathbb{Z}_2\text{.}$

Teorema$\PageIndex{1}$

Porque$n \geq 1\text{,}$$\lvert S_n\rvert =n!$ y para no$n \geq 3\text{,}$$S_n$ es abeliano.

Prueba: La primera parte del teorema se desprende de la regla extendida de los productos (ver Capítulo 2). Dejamos al lector los detalles de prueba de la segunda parte tras el siguiente indicio. Considera$f$ en$S_n$ dónde$f(1) = 2\text{,}$$f(2) = 3\text{,}$$f(3) = 1\text{,}$ y$f(j) = j$ para$3 < j \leq n\text{.}$ Por lo tanto la representación del ciclo de$f$ es$(1,2,3)\text{.}$ Ahora define$g$ de manera similar para que al comparar$f(g(1))$ y$g(f(1))$ obtengas resultados diferentes.

Notación de ciclo

Una segunda forma de describir una permutación es mediante ciclos, los cuales introduciremos primero con un ejemplo. Considere$f\in S_8$ definido usando la notación matricial ahora familiar:

\ begin {ecuación*} f=\ left (\ begin {array} {cccccccc} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8\\ 8 & 2 & 7 & 6 & 5 & 4 & 1 & 3\\ end {array}\ derecha)\ end {ecuación*}

Considera las imágenes de 1 cuando$f$ se aplica repetidamente. Las imágenes$f(1)\text{,}$$f(f(1))\text{,}$$f(f(f(1))), \ldots$ están$8, 3, 7, 1, 8, 3, 7,\ldots\text{.}$ En la Figura$\PageIndex{2}$ (a), esta situación está representada por una gráfica con los vértices 1, 8, 3 y 7 y muestra que los valores que obtienes al aplicar repetidamente$f$ ciclos a través de esos valores. Es por ello que nos referimos a esta parte de$f$ como un ciclo de longitud 4. Por supuesto, a partir de 8, 3 o 7 también se produce el mismo ciclo con solo el valor inicial cambiando.

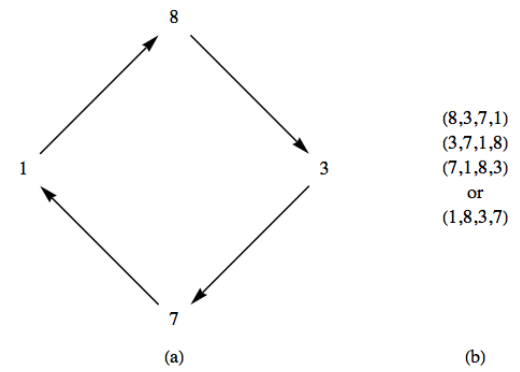$clipboard_ec0e238598d3084420f9956a0a90366a9.png$ Figura$\PageIndex{2}$: Representaciones de un ciclo de longitud 4

La figura$\PageIndex{2}$ (a) ilustra cómo se puede representar el ciclo de manera visual, pero es un poco incómodo de escribir. La parte (b) de la figura presenta una forma más universalmente reconocida de escribir un ciclo. En (b), un ciclo está representado por una lista donde la imagen de cualquier número de la lista es su sucesora. Además, el último número de la lista tiene como imagen el primer número.

Los otros elementos del dominio de nunca$f$ se alcanzan si se inicia en el ciclo$(1,8,3,7)\text{,}$ y así mirar las imágenes de estos otros números producirá números que son disjuntos del conjunto$\{1,8,3,7\}\text{.}$ Los otros ciclos disjuntos de$f$ son (2), (4, 6), y (5). Podemos expresarnos$f$ como producto de ciclos disjuntos:$f= (1, 8, 3, 7)(2)(4, 6)(5)$ o$f= (1,8,3,7)(4,6)\text{,}$ donde la ausencia de 2 y 5 implica que$f(2) = 2$ y$f(5) = 5\text{.}$

Nota$\PageIndex{2}$: Disjoint Cycles

Decimos que dos ciclos son disjuntos si no aparece ningún número en ambos ciclos, como es el caso en nuestras expresiones para$f$ arriba. Los ciclos disgregados se pueden escribir en cualquier orden. Así, también podríamos decir que$f=(4,6)(1,8,3,7)\text{.}$

Nota$\PageIndex{3}$: Composition of Permutations

Consideraremos ahora la composición de permutaciones escritas en forma cíclica con un ejemplo. Supongamos que$f = (1,8, 3, 7)(4, 6)$ y$g = (1, 5, 6)(8, 3, 7, 4)$ son elementos de$S_8\text{.}$ Para calcular$f\circ g\text{,}$ comenzamos con concatenación simple:

\[\label{eq:1}f\circ g=(1,8,3,7)(4,6)(1,5,6)(8,3,7,4)\]

Si bien esta es una expresión válida para$f \circ g\text{,}$ nuestro objetivo es expresar la composición como producto de ciclos disjuntos como$f$ y$g$ fueron escritos individualmente. Comenzaremos determinando el ciclo que contiene 1. Al combinar cualquier número de ciclos, siempre se leen de derecha a izquierda, como ocurre con todas las funciones. El primer ciclo en$\eqref{eq:1}$ no contiene 1; así pasamos al segundo. La imagen de 1 bajo ese ciclo es 5. Ahora pasamos al siguiente ciclo, buscando 5, que no aparece. El cuarto ciclo tampoco contiene un 5; entonces$f\circ g(1) = 5\text{.}$

En este punto, habríamos escrito “$f \circ g = (1,5 $” en papel. Repetimos los pasos para determinar$f\circ g(5)\text{.}$ Esta vez el segundo ciclo de$\eqref{eq:1}$ mueve 5 a 6 y luego el tercer ciclo mueve 6 a 4. Por lo tanto,$f\circ g(5) = 4\text{.}$ continuamos hasta que se complete el ciclo (1, 5, 4, 3) determinando que$f\circ g(3) = 1\text{.}$ El proceso se repite luego comenzando con cualquier número que no aparezca en el ciclo (s) que ya se hayan completado.

El resultado final para nuestro ejemplo es$f \circ g = (1, 5, 4, 3)(6, 8, 7)\text{.}$$f(2) = 2$ Since$g(2) = 2\text{,}$$f\circ g(2) = 2$ y y no necesitamos incluir el ciclo de un ciclo (2) en el resultado final, aunque se puede incluir.

Ejemplo$\PageIndex{3}$: Some Compositions

$\displaystyle (1, 2, 3, 4)(1, 2, 3, 4) = (1, 3)(2, 4)$
$(1, 4)(1, 3)(1, 2) = (1, 2, 3, 4)\text{.}$

Observe que la notación cíclica no indica el conjunto que se está permutando. Los ejemplos anteriores podrían ser en$S_5\text{,}$ donde la imagen de 5 es 5. Esta ambigüedad suele superarse dejando claro el contexto al inicio de una discusión.

Definición$\PageIndex{2}$: Transposition

Una transposición es un ciclo de longitud 2.

Observación$\PageIndex{1}$: About Transpositions

$f= (1, 4)$y$g=(4,5)$ son transposiciones en$S_5\text{.}$ Sin embargo,$f\circ g = (1,4, 5)$ y no$g \circ f = (1, 5, 4)$ son transposiciones; así, el conjunto de transposiciones no se cierra bajo composición. Ya que$f^2=f\circ f$ y ambos$g^2=g\circ g$ son iguales a la permutación de identidad,$f$ y$g$ son sus propios inversos. De hecho, cada transposición es su propia inversa.

Teorema$\PageIndex{2}$: Decomposition into Cycles

Cada ciclo de longitud mayor a 2 se puede expresar como un producto de transposiciones.

Prueba

Solo necesitamos indicar cómo se puede obtener el producto de las transposiciones. Es fácil verificar que un ciclo de longitud$k\text{,}$$\left(a_1, a_2, a_3, \ldots , a_k\right)\text{,}$ es igual al siguiente producto de$k-1$ transposiciones:

\ start {ecuación*}\ izquierda (a_1, a_k\ derecha)\ cdots\ izquierda (a_1, a_3\ derecha)\ izquierda (a_1, a_2\ derecha)\ end {ecuación*}

Por supuesto, un producto de ciclos puede escribirse como producto de transposiciones con la misma facilidad aplicando la regla anterior a cada ciclo. Por ejemplo,

\ start {ecuación*} (1, 3, 5, 7) (2, 4, 6) = (1, 7) (1, 5) (1, 3) (2, 6) (2, 4)\ end {ecuación*}

A diferencia de la situación con ciclos disjuntos, no somos libres de cambiar el orden de estas transposiciones.

La paridad de las permutaciones y el grupo alterno

Una descomposición de las permutaciones en transposiciones permite clasificar entonces e identificar una familia importante de grupos.

Las pruebas del siguiente teorema aparecen en muchos textos abstractos de álgebra.

Teorema$\PageIndex{3}$

Cada permutación en un conjunto finito puede expresarse como el producto de un número par de transposiciones o un número impar de transposiciones, pero no ambas.

El teorema$\PageIndex{3}$ sugiere que se$S_n$ puede dividir en sus elementos “pares” e “impares”. Por ejemplo, las permutaciones pares de$S_3$$r_2=(1,3,2)=(1,2)(1,3)\text{.}$ son$i\text{,}$$r_1=(1,2,3)=(1,3)(1,2)$ y forman un subgrupo,$\left\{i,r_1,r_2\right\}$ de$S_3\text{.}$

En general:

Definición $\PageIndex{3}$: The Alternating Group

Let$n \geq 2\text{.}$ El conjunto de permutaciones pares en$S_n$ es un subgrupo apropiado de$S_n$ llamado el grupo alterno en$\{1, 2, \ldots, n\}\text{,}$ denotado$A_n\text{.}$

Justificamos nuestra afirmación de que$A_n$ es un grupo:

Teorema$\PageIndex{4}$

Que$n \geq 2\text{.}$ El grupo alterno es de hecho un grupo y tiene orden$\frac{n!}{2}\text{.}$

Prueba

En esta prueba, los símbolos$s_i$ y$t_i$ representan transposiciones y$p\text{,}$$q$ son incluso enteros no negativos. Si$f, g \in A_n\text{,}$ podemos escribir las dos permutaciones como productos de números pares de transposiciones,$f=s_1s_2\cdots s_p$ y$g=t_1t_2\cdots t_q\text{.}$ Entonces

\ begin {ecuación*} f\ circ g=s_1s_2\ cdots s_pt_1t_2\ cdots t_q\ end {ecuación*}

Ya que$p+q$ es par,$f\circ g \in A_n\text{,}$ y$A_n$ está cerrado con respecto a la composición de la función. Con esto, hemos demostrado que$A_n$ es un subgrupo de$S_n$ por Teorema 11.5.2.

Para probar la aseveración final, deja$B_n$ ser el conjunto de permutaciones impares y dejar$\tau = (1,2)\text{.}$ Definir$\theta: A_n \to B_n$ por$\theta(f) = f\circ \tau\text{.}$ Supongamos que$\theta(f) = \theta(g)\text{.}$ Entonces$f\circ \tau = g\circ \tau $ y por la ley de cancelación correcta,$f = g\text{.}$ Por lo tanto,$\theta$ es una inyección. A continuación mostramos que también$\theta$ es una sobrejección. Si$h \in B_n\text{,}$$h$ es la imagen de un elemento de$A_n\text{.}$ Específicamente,$h$ es la imagen de$h\circ \tau\text{.}$

\ begin {ecuation*}\ begin {split}\ theta (h\ circ\ tau) & = (h\ circ\ tau)\ circ\ tau\\ & = h\ circ (\ tau\ circ\ tau)\ quad\ textrm {¿Por qué?} \\ & = h\ circ i\ quad\ textrm {¿Por qué?} \\ & = h\\\ final {división}\ final {ecuación*}

Dado que$\theta$ es una biyección,$\lvert A_n \rvert =\lvert B_n\rvert =\frac{n!}{2}\text{.}$

Ejemplo$\PageIndex{4}$: The Sliding Tile Puzzle

Considera los rompecabezas de azulejos deslizantes que se muestran en la Figura$\PageIndex{3}$. Cada cuadrado numerado es un azulejo y el cuadrado oscuro es un hueco. Cualquier baldosa que esté adyacente a la brecha puede deslizarse dentro de la brecha. En la mayoría de las versiones de este rompecabezas, los mosaicos están encerrados en un marco para que solo se puedan mover de la manera descrita anteriormente. El objeto del rompecabezas es disponer los mosaicos tal y como aparecen en la Configuración (a). Las configuraciones (b) y (c) son puntos de partida típicos. Proponemos mostrar por qué se puede resolver el rompecabezas empezando por (b), pero no con (c).

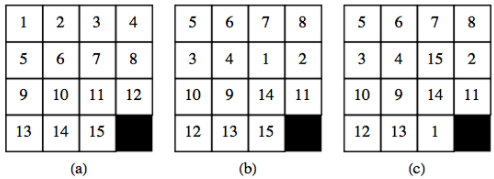$clipboard_e0fe47a67b122c6061c88edcd2affc1f3.png$ Figura$\PageIndex{3}$: Configuraciones del rompecabezas de baldosas deslizantes

Asociaremos un cambio en la configuración del rompecabezas con un elemento de$S_{16}\text{.}$ Imagine que un azulejo numerado 16 llena el hueco. Para cualquier configuración del rompecabezas, la identidad$i\text{,}$ es la función que deja la configuración “tal cual”. En general, si$f \in S_{16}\text{,}$ y$1 \leq k \leq 16\text{,}$$f(k)$ es la posición a la que$k$ se mueve la baldosa en posición por la$f$ que aparece en la posición de$k$ en configuración (a). Si llamamos a las funciones que, comenzando con configuration (a), resultan en configuraciones (b) y (c) por los nombres$f_1$ y$f_2\text{,}$ respectivamente,

\ begin {ecuación*} f_1 = (1, 5, 3, 7) (2, 6, 4, 8) (9, 10) (11, 14, 13, 12) (15) (16)\ end {ecuación*}

\ begin {ecuación*} f_2 = (1, 5, 3, 7, 15) (2, 6, 4, 8) (9, 10) (11, 14, 13, 12) (16). \ end {ecuación*}

¿Cómo podemos interpretar el movimiento de una baldosa como una permutación? Considera lo que sucede cuando el azulejo 12 de se$i$ desliza en el hueco. El resultado es una configuración que interpretaríamos como$(12,16)\text{,}$ una sola transposición. Ahora bien, si deslizamos el azulejo 8 a la posición 12, el resultado es o$(8, 16, 12)\text{.}$ Por lo tanto, al “intercambiar” los mosaicos 8 y 16, hemos implementado la función$(8, 12) (12, 16) = (8, 12, 16)\text{.}$

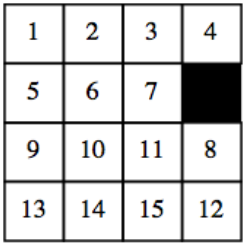$clipboard_ef4878acb2a6c0421ec4966032cf9ec64.png$ Figura$\PageIndex{4}$: La configuración$(8,12,16)$

Cada vez que deslizas un azulejo en la brecha, la nueva permutación es una transposición compuesta con la permutación antigua. Ahora observe que para comenzar con la configuración inicial y terminar después de un número finito de movimientos con la brecha en su posición original, se debe hacer un número par de movimientos. Así, la configuración correspondiente a cualquier permutación que deje 16 fijos no puede resolverse si la permutación es impar. Tenga en cuenta que$f_2$ es una permutación extraña; así, Puzzle (c) no se puede resolver. La prueba de que todas las permutaciones incluso, como$f_1\text{,}$ pueden resolverse, se deja al lector interesado para que la persiga.

Grupos Diedros

Observación$\PageIndex{2}$: Realization of Groups

A estas alturas ya hemos visto varias instancias en las que un grupo puede aparecer a través de una copia isomórfica de sí mismo en diversos escenarios. El ejemplo más simple es el grupo cíclico de orden 2. Cuando se menciona este grupo, naturalmente podríamos pensar en el grupo$\left[\mathbb{Z}_2;+_2\right]\text{,}$ pero en los grupos$[\{-1,1\};\cdot ]$ y$\left[S_2;\circ \right]$ son isomórficos a él. Ninguno de estos grupos es necesariamente más natural o importante que los demás. Cuál uses depende de la situación en la que te encuentres y a todos se les conoce como realizaciones del grupo cíclico de orden 2. La siguiente familia de grupos que estudiaremos, los grupos diedros, tiene dos realizaciones naturales, primero como permutaciones y segundo como simetrías geométricas.

La familia de grupos diedros está indexada por los enteros positivos mayores o iguales a 3. Para$k \geq 3\text{,}$$\mathcal{D}_k$ tendrá$2k$ elementos. Primero describimos los elementos y la operación sobre ellos usando geometría.

Podemos describir$\mathcal{D}_n$ en términos de simetrías de un$n$ -gon regular (triángulo$n = 3\text{:}$ equilátero,$n = 4\text{:}$ cuadrado, pentágono$n = 5\text{:}$ regular,$\ldots $). Aquí sólo nos concentraremos en el caso de$\mathcal{D}_4\text{.}$ Si un cuadrado se fija en el espacio, hay varios movimientos del cuadrado que, al final del movimiento, no cambiarán la posición aparente del cuadrado. Los cambios reales de posición se pueden ver si las esquinas del cuadrado están etiquetadas. En la Figura$\PageIndex{5}$ se muestra el esquema de etiquetado inicial, junto con los cuatro ejes de simetría del cuadrado.

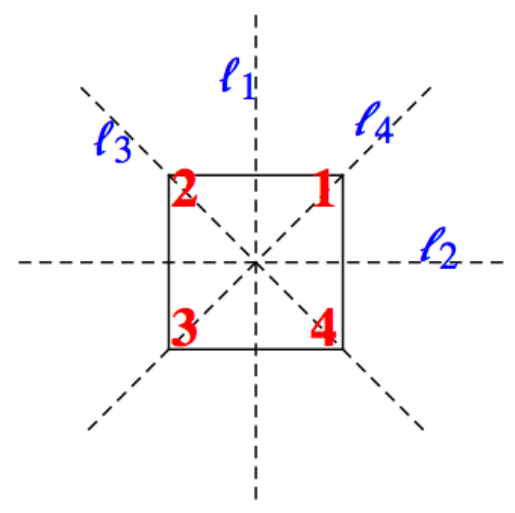$clipboard_e7f29c1a6bf681eda240dea44a5b5613b.png$ Figura$\PageIndex{5}$: Ejes de simetría del cuadrado

Podría valer la pena hacer un cuadrado como este con una hoja de papel. Tenga cuidado de etiquetar la parte posterior para que los números coincidan con el frente. Dos movimientos del cuadrado se considerarán equivalentes si el cuadrado está en la misma posición después de realizar cualquiera de los dos movimientos. Hay ocho movimientos distintos. Los primeros cuatro son$0{}^{\circ}\text{,}$$90{}^{\circ}\text{,}$$180{}^{\circ}\text{,}$ y rotaciones en$270{}^{\circ}$ sentido horario del cuadrado, y los otros cuatro son los$180{}^{\circ}$ volteretas a lo largo de los ejes$l_1\text{,}$$l_2\text{,}$$l_3\text{,}$ y$l_4\text{.}$ llamaremos a las rotaciones$i, r_1\text{,}$$r_2\text{,}$ y$r_3\text{,}$ respectivamente, y a las voltea$f_1\text{,}$$f_2\text{,}$$f_3\text{,}$ y$f_4\text{,}$ respectivamente. Figura$\PageIndex{6}$ ilustra$r_1$ y$f_1\text{.}$ Para futura referencia, también incluimos las permutaciones a las que corresponden.

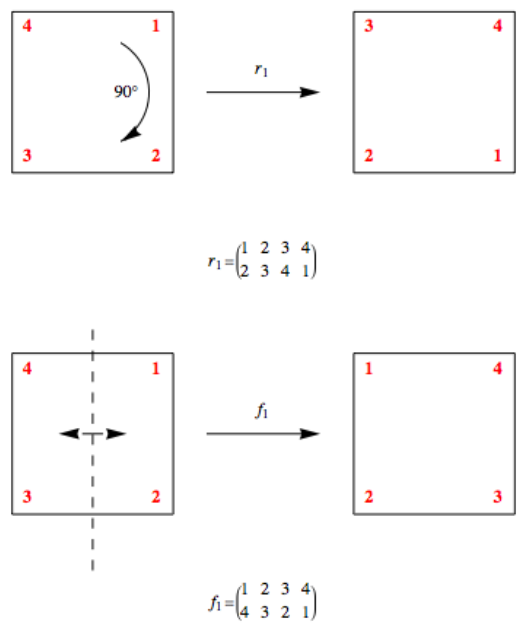$clipboard_e621f265899fef9b8660a1a925ce59d6a.png$ Figura$\PageIndex{6}$: Dos elementos de$\mathcal{D}_4$

¿Cuál es la operación en este conjunto de simetrías? Llamaremos a la operación “seguida de” y usaremos el símbolo$*$ para representarla. La operación consistirá en combinar movimientos, aplicando movimientos de derecha a izquierda, como con funciones. Vamos a ilustrar cómo$*$ se calcula encontrando$r_1*f_1\text{.}$ Comenzando con la configuración inicial, si se realiza el$f_1$ movimiento, y luego inmediatamente se realiza$r_1$ sobre el resultado, obtenemos la misma configuración que si acabamos de realizar$f_4\text{,}$ que es voltear el cuadrado a lo largo de la línea $l_4\text{.}$Por lo tanto,$r_1*f_1 = f_4\text{.}$ Una observación importante es que$f_1*r_1 \neq f_4\text{,}$ significa que este grupo es no abeliano. Se anima al lector a verificar esto por su cuenta.

También podemos realizar los grupos diedros como permutaciones. Para cualquier movimiento simétrico del cuadrado podemos asociar con él una permutación. En el caso de$\mathcal{D}_4\text{,}$ las imágenes de cada uno de los números del 1 al 4 son las posiciones sobre el cuadrado a las que se mueve cada una de las esquinas 1 a 4. Por ejemplo, ya que la esquina 4 se mueve a la posición 1 al realizar$r_1\text{,}$ la función correspondiente mapeará 4 a 1. Además, 1 se mapea a 2, 2 a 3 y 3 a 4. Por lo tanto,$r_1$ es el ciclo$(1,2,3,4)$. El flip$f_1$ transpone dos pares de esquinas y corresponde a$(1,4)(2,3)\text{.}$ Si queremos combinar estas dos permutaciones, usando los mismos nombres que con movimientos, obtenemos

\ start {ecuación*} r_1\ circ f_1= (1,2,3,4)\ circ (1,4) (2,3) = (1) (2,4) (3) = (2,4)\ final {ecuación*}

Observe que esta permutación corresponde con el flip$f_4\text{.}$

Aunque$\mathcal{D}_4$ no es cíclico (ya que no es abeliano), se puede generar a partir de los dos elementos$r_1$ y$f_1\text{:}$

\ begin {ecuación*}\ mathcal {D} _4=\ izquierda\ langle r_1, f_1\ derecha\ rangle =\ izquierda\ {i, r_1, r_1 {} ^2, r_1 {} ^3, f_1, r_1\ circ f_1, r_1 {} ^2\ circ f_1, r_1 {} 3\ circ f_1\ derecho\}\ final {ecuación*}

Es bastante fácil describir cualquiera de los grupos diedros de manera similar. Aquí está la definición formal

Definición $\PageIndex{4}$: Dihedral Group

Dejar$n$ ser un entero positivo mayor o igual a 3. Si$r= (1,2, \ldots , n)\text{,}$ un$n$ -ciclo, y$f= (1,n)(2,n-1)\ldots$ Entonces

\ start {ecuación*}\ mathcal {D} _n=\ langle r, f\ rangle =\ izquierda\ {i, r, r^2,\ ldots, r^ {n-1}, f, r\ circ f, r^2\ circ f,\ ldots, r^ {n-1}\ circ f\ derecha\}\ end {ecuación*}

es el grupo diedro$n$ th.

Nota$\PageIndex{4}$: Caution

Podrías notar que utilizamos un guión$D\text{,}$$\mathcal{D}\text{,}$ para los grupos diedros. Ocasionalmente se puede ver un ordinario$D$ en otras fuentes para los grupos diedros. No lo confundas con el conjunto de divisores del$n\text{,}$ que denotamos por$D_n\text{.}$ Normalmente el contexto de la discusión debe dejar$D_n$ claro el significado de.

Ejemplo$\PageIndex{5}$: A Letter-Facing Machine

Una aplicación de$\mathcal{D}_4$ es en el diseño de una máquina de revestimiento de letras. Imagina letras entrando en una cinta transportadora para ser matasellos. Se colocan en la cinta transportadora al azar para que dos lados queden paralelos a la cinta. Supongamos que un posmarcador puede reconocer un sello en la esquina superior derecha del sobre, en el lado hacia arriba. En la Figura$\PageIndex{7}$, se muestra una secuencia de máquinas que reconocerán un sello en cualquier letra, sin importar qué posición en la que comience la letra. La letra$P$ significa un posmarcador. Las letras$R$ y el$F$ soporte para máquinas giratorias y volteadoras que realizan los movimientos de$r_1$ y$f_1\text{.}$

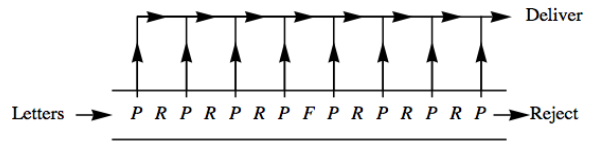$clipboard_ef5165616a5431e5a8c1709f8c96a107a.png$ Figura$\PageIndex{7}$: Un facer de letras

Las flechas apuntando hacia arriba indican que si una letra tiene matasellos, se saca de la cinta transportadora para su entrega. Si una letra llega al final, no debe tener sello. Se han diseñado máquinas de revestimiento de letras como esta (ver [16]). Una consideración económica es que$R$ -las máquinas tienden a costar más que$F$ -máquinas. $R$-las máquinas también tienden a dañar más letras. Teniendo en cuenta estos hechos, se invita al lector a diseñar una mejor máquina de revestimiento de letras. Supongamos que$R$ -costo de$F$ máquinas$\$800$ y -costo de máquinas$\$500\text{.}$ Asegúrese de que todas las esquinas de las letras entrantes serán examinadas a medida que bajan por la cinta transportadora.

Ejercicios

Ejercicio$\PageIndex{1}$

Dado$f=\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \\ \end{array} \right)\text{,}$$g=\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \\ \end{array} \right)\text{,}$ y$h=\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 2 & 4 & 1 \\ \end{array} \right)\text{,}$ cómpulico

$\displaystyle f\circ g$
$\displaystyle g\circ h$
$\displaystyle (f\circ g)\circ h$
$\displaystyle f\circ (g\circ h)$
$\displaystyle h^{-1}$
$\displaystyle h^{-1} \circ g\circ h$
$\displaystyle f^{-1}$

Contestar

$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 4 & 3 & 1 & 2 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 4 & 2 & 1 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 4 & 2 & 1 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 4 & 2 & 1 & 3 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 1 & 4 & 2 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \\ \end{array} \right)$

Ejercicio$\PageIndex{2}$

Escribir$f\text{,}$$g\text{,}$ y$h$ desde Ejercicio$\PageIndex{1}$ como productos de ciclos disjuntos y determinar si cada uno es impar o par.

Ejercicio$\PageIndex{3}$

¿Los coconjuntos izquierdos de$A_3=\left\{i,r_1,r_2\right\}$ over$S_3$ forman un grupo bajo la operación inducida en los cosets izquierdos de$A_3\text{?}$ ¿Qué pasa con los coconjuntos izquierdos de$\left\langle f_1\right\rangle\text{?}$

Contestar: $S_3/A_3$es un grupo de orden dos. La operación en los cosets izquierdos de no$H=\left\langle f_1\right\rangle$ está bien definida y por lo tanto no se puede formar un grupo a partir de cosets izquierdos de$H\text{.}$

Ejercicio$\PageIndex{4}$

En su realización como permutaciones, el grupo diedro$\mathcal{D}_3$ es igual a ¿$S_3\text{.}$Se puede dar una explicación geométrica por qué? ¿Por qué no es$\mathcal{D}_4$ igual a$S_4\text{?}$

Ejercicio $\PageIndex{5}$

Completar la lista de elementos de$\mathcal{D}_4$ y escribir una tabla para el grupo en su realización como simetrías.
Enumere los subgrupos de$\mathcal{D}_4$ en un diagrama de celosía. ¿Son todas cíclicas? ¿A qué grupos más simples son los subgrupos de$\mathcal{D}_4$ isomórficos?

Contestar

$\mathcal{D}_4 = \left\{i, r, r^2, r^3, f_1, f_2, f_3, f_4\right\}$¿Dónde$i$ está la función de identidad,$r=\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \\ \end{array} \right)\text{,}$ y

\ begin {ecuación*}\ begin {array} {cc} f_1 =\ left (\ begin {array} {cccc} 1 & 2 & 3 & 4\\ 4 & 3 & 2 & 1\\ end {array}\ right) & f_2 =\ left (\ begin {array} {cccc} 1 & 2 & 3 & 4\\ 2 & 1 & 4 & 3\\ end {array}\ derecha)\\ f_3 =\ left (\ begin {array} {cccc} 1 y 2 y 3 & 4\\ 3 & 2 & 1 & 4\\\ end {array}\ derecha) & f_4 =\ left (\ begin {array} {cccc} 1 & 2 & 3 & 4\\ 1 & 4 & 3 & 2\\ end {array}\ right)\\ end {array}\ end {array}\ end {ecuación*}

La tabla de operaciones para el grupo es

\ begin {ecuación*}\ begin {array} {c|c}\ circ &\ textrm {}\ begin {array} {cccccc} i & r & r^2 & r^3 & f_1 & f_2 & f_3 & f_4\\ end {array}\\ hline\ begin {array} {c} i\\ r\ r^2\\ r^3\\ f_1\\ f_2\\ f_3\\ f_4\\\ end {array} &\ begin {array} {cccccccc} i & r & r^2 & ; r^3 & f_1 & f_2 & f_3 & f_4\\ r & r^2 & r^3 & i & f_4 & f_3 & f_1 & f_2\\ r^2 & r^3 & i & r & f_2 & f_1 & f_4 & f_3\\ r^3 & i & r & r^2 & f_3 & f_3 & f_3 & f_3 & i & r _4 y f_2 y f_1\\ f_1 y f_3 y f_2 y f_4 e i y ; r^2 & r & r^3\\ f_2 & f_4 & f_1 & f_3 & r^2 & i & r^3 & r\\ f_3 & f_2 & f_4 & f_1 & r^3 & r & i & r^2\ f_4 & f_1 & f_3 & f_2 & r & r^3 & r^2 & i\\\ end {array}\\\ end {array}\ end {ecuación*}

Un diagrama reticular de sus subgrupos es

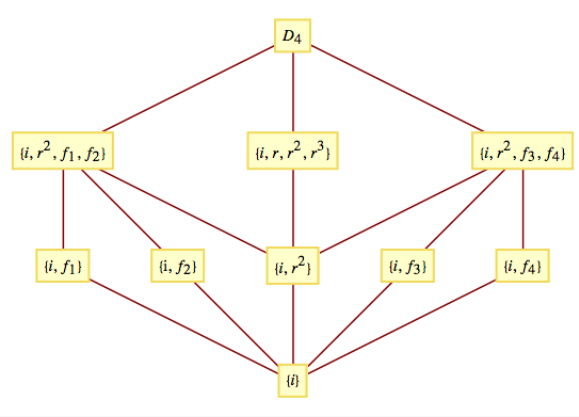$clipboard_e1b298e40762e846d0a25ba928ca9043e.png$ Figura$\PageIndex{8}$: Subgrupos de$\mathcal{D}_4$

Todos los subgrupos apropiados son cíclicos excepto$\left\{i,r^2,f_1,f_2\right\}$$\textrm{ }\textrm{ }$ y$\left\{i,r^2,f_3,f_4\right\}\text{.}$ Cada subgrupo de 2 elementos es isomórfico a$\mathbb{Z}_2$;$\left\{i,r,r^2,r^3\right\}$ es isomórfico a$\mathbb{Z}_4$; y$\left\{i,r^2,f_1,f_2\right\}$$\textrm{ }\textrm{ }$ y$\left\{i,r^2,f_3,f_4\right\}$ son isomórficos para$\mathbb{Z}_2\times \mathbb{Z}_2\text{.}$

Ejercicio$\PageIndex{6}$

Diseñe una mejor máquina de revestimiento de letras (ver Ejemplo$\PageIndex{5}$). ¿Cómo se puede verificar que una máquina de cara a letras efectivamente verifica cada esquina de una carta? ¿Se puede hacer en papel sin realmente enviar cartas a través de él?

Ejercicio$\PageIndex{7}$

Demostrar por inducción que si$r \geq 1$ y cada uno$t_i\text{,}$ es una transposición, entonces$\left(t_1\circ t_2\circ \cdots \circ t_r\right){}^{-1}=t_r\circ \cdots \circ t_2\circ t_1$

Contestar: Una solución es citar el Ejercicio 11.3.3 al final de la Sección 11.3. Se puede aplicar directamente a este problema. Una prueba de inducción del problema que nos ocupa sería casi idéntica a la prueba de la declaración más general. $\left(t_1t_2\cdots t_r\right){}^{-1}= t_r{}^{-1}\cdots t_2{}^{-1}t_1{}^{-1}\quad\textrm{ by Exercise 11.3.3 of Section 11.3}\\ \\ \quad \quad = t_r\cdots t_2t_1\textrm{ }\textrm{ since} \textrm{ each} \textrm{ transposition} \textrm{ inverts} \textrm{ itself}.\textrm{ }\blacksquare$

Ejercicio$\PageIndex{8}$

¿En cuántos elementos hay$\mathcal{D}_5$? Describirlos geométricamente.

Ejercicio$\PageIndex{9}$

Completar la prueba del Teorema$\PageIndex{1}$.

Contestar

Parte I: Eso se$\lvert S_k \rvert = k!$ desprende de la Regla de Productos.

Parte II: Dejar$f$ ser la función definida en$\{1,2,\textrm{ ...}, n\}$ por$f(1)=2\text{,}$$f(2)=3\text{,}$$f(3)=1\text{,}$ y$f(j) =j$ para$4\leq j\leq n\text{;}$ y dejar$g$ ser definida por$g(1) = 1\text{,}$$g(2) = 3\text{,}$$g(3) = 2\text{,}$ y$g(j) =j$ para$4\leq j\leq n\text{.}$ Tenga en cuenta que$f$ y$g$ son elementos de$S_n\text{.}$ Siguiente ,$(f\circ g)(1) = f(g(1)) = f(1) = 2\text{,}$ mientras que$(g \circ f)(1) = g(f(1)) = g(2) = 3\text{,}$ por lo tanto$f\circ g\neq g\circ f$ y no$S_n$ es abeliano para cualquier$n \geq 3\text{.}$

Ejercicio$\PageIndex{10}$

¿Cuántos cosets de izquierda$A_n\text{,}$$n\geq 2$ tiene?

Ejercicio$\PageIndex{11}$

Demostrar que$f\circ r= r^{n-1}\circ f$ en$\mathcal{D}_n\text{.}$

Ejercicio$\PageIndex{12}$

Demostrar que los rompecabezas de baldosas correspondientes a$A_{16}\cap \left\{ \left.f \in S_{16} \right| f(16) = 16\right\}$ son solucionables.
Si$f(16)\neq 16\text{,}$ ¿cómo se puede determinar si$f$ el rompecabezas es solucionable?

Ejercicio$\PageIndex{13}$

Demostrar que$S_3$ es isomórfico$R_3\text{,}$ al grupo de$3 \times 3$ matrices de gradas (ver Sección 11.2 ejercicios).
Demostrar que para cada uno$n \geq 2\text{,}$$R_n$ es isomórfico a$S_n\text{.}$

Contestar

Ambos grupos son no abelianos y de orden 6; por lo que deben ser isomórficos, ya que solo existe uno de esos grupos hasta el isomorfismo. La función$\theta:S_3\to R_3$ defined by $\begin{array}{cc} \theta(i)=I & \theta\left(f_1\right)=F_1 \\ \theta\left(r_1\right)=R_1 & \theta\left(f_2\right)=F_2 \\ \theta\left(r_2\right)=R_2 & \theta\left(f_3\right)=F_3 \\ \end{array}$ is an isomorphism,
Recordemos que como cada función es una relación, es natural traducir funciones a matrices booleanas. Supongamos que$f\in S_n\text{.}$ vamos a definir su imagen,$\theta(f)\text{,}$ por
\ begin {ecuation*}\ theta (f) _ {kj} =1\ textrm {}\ Leftrightarrow\ textrm {} f (j) =k\ end {ecuación*}
Eso$\theta$ es una biyección que se desprende de la existencia de$\theta^{-1}\text{.}$ If$A$ es una matriz de grada,
\ begin {ecuation*}\ begin {split}\ theta^ {-1} (A) (j) =k &\ Leftrightarrow\ textrm {}\ textrm {los} 1\ textrm {in}\ textrm {columna} j\ textrm {de} A\ textrm {aparece}\ textrm {en}\ textrm {fila}\\ &\ Leftrightarrow A_ {kj} =1\ end {split}\ end {equation*}
Para $f,g\in S_n\text{,}$
\ begin {ecuación*}\ begin {split}\ theta (f\ circ g) _ {kj} = 1 &\ Leftrightarrow\ textrm {} (f\ circ g) (j) =k\\ &\ Leftrightarrow\ existe l\ textrm {tal que} g (j) =l\ textrm {y} f (l) =k\\ &\ Leftrightarrow\ existe l\ textrm {tal que}\ theta (g) _ {lj} =1\ textrm {y}\ textrm {}\ theta (f) _ {kl} =1\\ &\ Leftrightarrow (\ theta (f)\ theta (g)) _ {kj} =1\ end {split}\ end {equation*}
Por lo tanto,$\theta$ es un isomorfismo.

\(i =\left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \\ \end{array} \right)\)	\(r_1=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 3 & 1 \\ \end{array} \right)\)	\(r_2=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 1 & 2 \\ \end{array} \right)\)
\(f_1=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 3 & 2 \\ \end{array} \right) \)	\(f_2=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \\ \end{array} \right)\)	\(f_3=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 1 & 3 \\ \end{array} \right)\)