15.5: Teoría de Codificación, Códigos de Grupo

Última actualización
Guardar como PDF

Page ID: 117155

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Problema de transmisión

En esta sección, presentaremos las ideas básicas involucradas en la teoría de la codificación y consideraremos soluciones de un problema de codificación por medio de códigos de grupo.

Imagínese una situación en la que se esté transmitiendo información entre dos puntos. La información toma la forma de pulsos altos y bajos (por ejemplo, ondas de radio o corrientes eléctricas), que etiquetaremos 1 y 0, respectivamente. A medida que estos pulsos son enviados y recibidos, se agrupan en bloques de longitud fija. La longitud determina cuánta información se puede contener en un bloque. Si la longitud es$r\text{,}$ hay$2^r$ diferentes valores que puede tener un bloque. Si la información que se envía toma la forma de texto, cada bloque podría ser un carácter. En ese caso, la longitud de un bloque puede ser siete, de manera que los valores de$2^7 = 128$ bloque pueden representar letras (tanto mayúsculas como minúsculas), dígitos, puntuación, etc. Durante la transmisión de datos, el ruido puede alterar la señal para que lo que se recibe difiera de lo que se envía. La figura$\PageIndex{1}$ ilustra el problema que se puede encontrar si la información se transmite entre dos puntos.

$clipboard_e18c4e20ab50f2d417976e617d1260b67.png$ Figura$\PageIndex{1}$: Una transmisión ruidosa

El ruido es un hecho de la vida para cualquiera que intente transmitir información. Afortunadamente, en la mayoría de las situaciones, podríamos esperar que un alto porcentaje de los pulsos que se envían se reciban adecuadamente. Sin embargo, cuando se transmiten grandes cantidades de pulsos, generalmente hay algunos errores debido al ruido. Para lo que resta de la discusión, haremos suposiciones sobre la naturaleza del ruido y el mensaje que queremos enviar. En adelante, nos referiremos a los pulsos como bits.

Supondremos que nuestra información está siendo enviada a lo largo de un canal simétrico binario. Con esto, queremos decir que cualquier bit único que se transmita será recibido incorrectamente con una cierta probabilidad fija,$p\text{,}$ independiente del valor del bit. La magnitud de$p$ suele ser bastante pequeña. Para ilustrar el proceso, asumiremos aquello$p = 0.001\text{,}$ que, en el mundo real, se consideraría algo grande. Ya que$1 - p = 0.999\text{,}$ podemos esperar$99.9\%$ de todos los bits que se reciban correctamente.

Supongamos que nuestro mensaje consta de 3,000 bits de información, para ser enviados en bloques de tres bits cada uno. Se considerarán dos factores en la evaluación de un método de transmisión. El primero es la probabilidad de que el mensaje se reciba sin errores. El segundo es el número de bits que se transmitirán para poder enviar el mensaje. Esta cantidad se llama la velocidad de transmisión:

\ begin {ecuación*}\ textrm {Tasa} =\ frac {\ textrm {Longitud del mensaje}} {\ textrm {Número de bits transmitidos}}\ end {ecuación*}

Como cabría esperar, a medida que ideamos métodos para mejorar la probabilidad de éxito, la tasa disminuirá.

Supongamos que ignoramos el ruido y transmitimos el mensaje sin ninguna codificación. La probabilidad de éxito es$0.999^{3000}= 0.0497124\text{.}$ Por lo tanto, solo recibimos con éxito el mensaje en una forma totalmente correcta menos que$5\%$ de las veces. La tasa de$\frac{3000}{3000} = 1$ ciertamente no compensa esta mala probabilidad.

Nuestra estrategia para mejorar nuestras posibilidades de éxito será enviar un mensaje codificado a través del canal simétrico binario. La codificación se realizará de tal manera que se puedan identificar y corregir pequeños errores. Esta idea se ilustra en la Figura$\PageIndex{2}$.

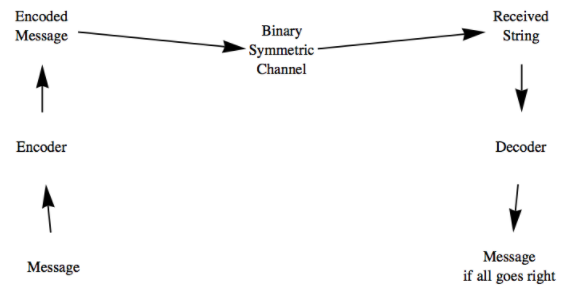$clipboard_e1db747a127cf5933e608483ca9935140.png$ Figura$\PageIndex{2}$: El proceso de codificación

En nuestros ejemplos, las funciones que corresponderán a nuestros dispositivos de codificación y decodificación serán todos homomorfismos entre productos cartesianos de$\mathbb{Z}_2\text{.}$

Detección de errores

Supongamos que cada bloque de tres bits$a = \left(a_1, a_2 , a_3 \right)$ está codificado con la función$e: \mathbb{Z}_2{}^3\to \mathbb{Z}_2{}^4\text{,}$ donde

\ begin {ecuación*} e (a) =\ izquierda (a _1, a _2, a _3, a_1+_2a_2+_2a_3\ derecha)\ end {ecuación*}

Cuando se recibe el bloque codificado, los cuatro bits probablemente serán todos correctos (son correctos aproximadamente$99.6\%$ de la vez), pero el bit agregado que se envía permitirá detectar errores únicos en el bloque. Tenga en cuenta que cuando$e(a)$ se transmite, la suma de sus componentes es$a_1+_2 a_2 +_2 a_3+_2 \left( a_1+_2 a_2+_2 a_3\right)= 0\text{,}$ ya que$a_i+a_i=0$ en$\mathbb{Z}_2\text{.}$

Si cualquier bit es iluscado por el ruido, la suma de los bits recibidos será 1. El último bit de$e(a)$ se llama el bit de paridad. Se produce un error de paridad si la suma de los bits recibidos es 1. Dado que más de un error es poco probable cuando$p$ es pequeño, se puede detectar un alto porcentaje de todos los errores.

En el extremo receptor, la función de decodificación actúa sobre el bloque de cuatro bits$b = \left(b_1,b _2 ,b_3,b_4 \right)$ con la función$d: \mathbb{Z}_2{}^4\to \mathbb{Z}_2^4\text{,}$ donde

\ begin {ecuación*} d (b) =\ izquierda (b_1, b _2, b_3, b_1+_2b _2 +_2b_3+_2b_4\ derecha)\ end {ecuación*}

El cuarto bit se llama bit de comprobación de paridad. Si no se produce ningún error de paridad, los tres primeros bits se registran como parte del mensaje. Si se produce un error de paridad, asumiremos que se puede solicitar una retransmisión de ese bloque. Esta solicitud puede tomar la forma de tener automáticamente el bit de verificación de paridad$d(b)$ enviado de vuelta a la fuente. Si se recibe 1, se retransmite el bloque anterior; si se recibe 0, se envía el siguiente bloque. Esta suposición de comunicación bidireccional es significativa, pero es deseable hacer útil este sistema de codificación. Es razonable esperar que la probabilidad de un error de transmisión en la dirección opuesta también sea 0.001. Sin entrar en los detalles, informaremos que la probabilidad de éxito es de aproximadamente 0.990 y la tasa es aproximadamente 3/5. La tasa incluye la transmisión del bit de comprobación de paridad a la fuente.

Corrección de errores

A continuación, consideraremos un proceso de codificación que pueda corregir errores en el extremo receptor para que solo se necesite comunicación unidireccional. Antes de comenzar, recordemos que cada elemento de$\mathbb{Z}_2{}^n\text{,}$$n \geq 1\text{,}$ es su propio inverso; es decir,$-b = b\text{.}$ Por lo tanto,$a - b = a + b\text{.}$

Los bloques de mensajes ruidosos de tres bits son difíciles de transmitir porque son muy similares entre sí. Si$a$ y$b$ están en$\mathbb{Z}_2{}^3\text{,}$ su diferencia,$a +_2 b\text{,}$ pueden pensarse como una medida de lo cerca que están. Si$a$ y$b$ difieren en una sola posición de bit, un error puede cambiar uno a otro. La codificación que vamos a introducir toma un bloque$a = \left(a_1, a_2, a_3 \right)$ y produce un bloque de longitud 6 llamado la palabra código de Las palabras de$a\text{.}$ código se seleccionan para que estén más alejadas entre sí de lo que están los mensajes. De hecho, cada palabra de código diferirá entre sí en al menos tres bits. Como resultado, cualquier error no empujará una palabra de código lo suficientemente cerca de otra palabra de código como para causar confusión. Ahora para los detalles.

Deja$G=\left( \begin{array}{cccccc} 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 \\ \end{array} \right)\text{.}$ Llamamos a$G$ la matriz generadora para el código, y dejemos$a = \left(a_1, a_2, a_3 \right)$ ser nuestro mensaje.

Definir$e : \mathbb{Z}_2{}^3 \to \mathbb{Z}_2{}^6$ por

\ begin {ecuación*} e (a) = a G =\ izquierda (a_1, a_2, a_3, a_4, a_5, a_6\ derecha)\ end {ecuación*}

donde

\ begin {ecuación*}\ begin {array} {r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {}} a_4 &= & a_1 & {} +_2 {} & a_2 & &\ a_5 &= & a_1 & & & & {} +_2 {} & a_3\ a_6 &= & & a_2 & {} +_2 {} & a_3\\\ end {array}\ end {ecuación*}

Observe que$e$ es un homomorfismo. Además, si$a$ y$b$ son elementos distintos de$\mathbb{Z}_2{}^3\text{,}$ entonces$c = a + b$ tiene al menos una coordenada igual a 1. Ahora considera la diferencia entre$e(a)$ y$e(b)\text{:}$

\ comenzar {ecuación*}\ comenzar {dividir} e (a) + e (b) &= e (a + b)\\ & = e (c)\\ & =\ izquierda (d_1, d_2, d_3, d_4, d_5, d_6\ derecha)\\ final {división}\ final {ecuación*}

Ya sea$c$ que tenga 1, 2 o 3,$e(c)$ debe tener al menos tres. Esto se puede ver considerando los tres casos por separado. Por ejemplo, si$c$ tiene uno único, dos de los bits de paridad también son 1. Por lo tanto,$e(a)$ y$e(b)$ difieren en al menos tres bits.

Consideremos ahora el problema de decodificar las palabras de código. Imagínese que una palabra clave,$e(a)\text{,}$ se transmite, y$b= \left(b_1, b_2, b_3,b_4, b_5, b_6\right)$ se recibe. En el extremo receptor, conocemos la fórmula para$e(a)\text{,}$ y si no se ha producido ningún error en la transmisión,

\ begin {ecuación*}\ begin {array} {c} b_1= a_1\\ b_2=a_2\\ b_3=a_3\\ b_4=a_1+_2a_2\\ b_5=a_1+_2a_3\\ b_6=a_2+_2a_3\\ end {array}\ Rightarrow\ begin {array} {r@} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} r@ {} b_1 & +_2 y b_2 & &+_2& b_4& & & & & &=0\\ b_1 & & & & amp; +_2 &b_3& & & +_2& b_5 & & &=0\\ & & b_2 & +_2 &b_3& & & & & & &+_2 &b_6&=0\\\ end {array}\ end {ecuación*}

Las tres ecuaciones de la derecha se denominan ecuaciones de comprobación de paridad. Si alguno de ellos no es cierto, se ha producido un error. Esta comprobación de errores se puede describir en forma de matriz.

Let

\ begin {ecuación*} P=\ left (\ begin {array} {ccc} 1 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 1\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 1\\ end {array}\\ derecha)\ end {ecuación*}

$P$se llama la matriz de comprobación de paridad para este código. Ahora$p(b) = b P\text{.}$ definimos$p:\mathbb{Z}_2{}^6 \to \mathbb{Z}_2{}^3$ por Llamamos$p(b)$ al síndrome del bloqueo recibido. Por ejemplo,$p(0,1,0,1,0,1)=(0,0,0)$ y$p(1,1,1,1,0,0)=(1,0,0)$

Tenga en cuenta que también$p$ es un homomorfismo. Si el síndrome de un bloqueo es$(0, 0, 0)\text{,}$ podemos estar casi seguros de que el bloque de mensajes es$\left(b_1, b_2, b_3\right)\text{.}$

A continuación pasamos al método de corrección de errores. A pesar de que solo hay ocho palabras de código, una por cada valor de bloque de tres bits, el conjunto de posibles bloques recibidos es$\mathbb{Z}_2{}^6\text{,}$ con 64 elementos. Supongamos que no$b$ es una palabra de código, sino que difiere de una palabra de código exactamente en un bit. En otras palabras, es el resultado de un solo error en la transmisión. Supongamos que$w$ es la palabra clave a la que$b$ está más cerca y que difieren en el primer bit. Entonces$b + w = (1, 0, 0, 0, 0, 0)$ y

\ begin {ecuation*}\ begin {split} p (b) & = p (b) + p (w)\ quad\ textrm {since} p (w) = (0, 0, 0)\\ &=p (b+w)\ quad\ textrm {desde} p\ textrm {es un homomorfismo}\\ & =p (1,0,0,0,0)\\ & = (1,1,0)\\\ end {split}\ end {ecuación*}

Tenga en cuenta que no hemos especificado$b$ o$w\text{,}$ solo que difieren en el primer bit. Por lo tanto, si$b$ se recibe, probablemente hubo un error en el primer bit y$p(b) = (1, 1, 0)\text{,}$ la palabra de código transmitida fue probablemente$b + (1, 0, 0, 0, 0, 0)$ y el bloque de mensaje fue$\left(b_1+_2 1, b_2, b_3\right)\text{.}$ El mismo análisis se puede hacer si$b$ y$w$ difieren en cualquiera de los otros cinco bits.

Este proceso puede describirse en términos de cosets. Dejar$W$ ser el conjunto de palabras clave; es decir,$W = e\left(\mathbb{Z}_2{}^3 \right)\text{.}$ Dado que$e$ es un homomorfismo,$W$ es un subgrupo de$\mathbb{Z}_2{}^6\text{.}$ Considerar el grupo factor$\left.\mathbb{Z}_2{}^6\right/W\text{:}$

\ begin {ecuación*}\ lvert\ mathbb {Z} _2 {} ^6/W\ rvert =\ frac {\ lvert\ mathbb {Z} _2 {} ^6\ rvert} {\ lvert W\ rvert} =\ frac {64} {8} =8\ final {ecuación*}

Supongamos que$b_1$ y$b_2$ son representantes del mismo coset. Entonces$b_1= b_2+w$ para algunos$w$ en$W\text{.}$ Por lo tanto,

\ begin {ecuation*}\ begin {split} p\ left (b _1\ right) &= p\ left (b_1\ right) + p (w)\ quad\ textrm {since} p (w) = (0, 0, 0)\\ &= p\ left (b_1 + w\ right)\\ &= p\ left (b_2\ right)\\ end dividir}\ end {ecuación*}

y así$b_1$ y$b_2$ tienen el mismo síndrome.

Por último, supongamos que$d_1$ y$d_2$ son distintos y ambos tienen sólo una sola coordenada igual a 1. Entonces$d_1+d_2$ tiene exactamente dos. Tenga en cuenta que la identidad de$\mathbb{Z}_2{}^6\text{,}$$(0, 0, 0, 0, 0, 0)\text{,}$ debe estar en$W\text{.}$$d_1+d_2$ Since difiere de la identidad por dos bits,$d_1+d_2 \notin W\text{.}$ Por lo tanto$d_1$ y$d_2$ pertenecen a coconjuntos distintos. El razonamiento anterior sirve como prueba del siguiente teorema.

Teorema$\PageIndex{1}$

Existe un sistema de distinguidos representantes de$\left.\mathbb{Z}_2{}^6\right/W$ tal manera que cada uno de los bloques de seis bits que tienen un solo 1 es un distinguido representante de su propio coset.

Ahora podemos describir el proceso de corrección de errores. Primero empareja cada uno de los bloques con un solo 1 con su síndrome. Además, emparejar la identidad de$W$ con el síndrome$(0, 0, 0)$ como se muestra en la siguiente tabla. Ya que hay ocho cosets de$W\text{,}$ seleccionar cualquier representante del octavo coset a distinguir. Este es el coset con síndrome$(1, 1, 1)\text{.}$

\ begin {ecuación*}\ begin {array} {c|c}\ begin {array} {c}\ textrm {síndrome}\\ hline\ begin {array} {ccc} 0 & 0 & 0\\ 1 & 0\\ 1 & 0\\ 1 & 0 & 1\\ 0 & 1\\ 1 & 1\\ 1 & 0 & 0 & 0\ 0 & 1 & 0\ 1 & 1 & 1\\\ end {array}\\\ end {array} &\ begin { array} {c}\ textrm {Error}\ textrm {Corrección}\\\ hline\ begin {array} {cccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0 & 0 & 1\\\ end {array}\\ end {array}\\ end {array}\ end {ecuación*}

Cuando$b$ se recibe el bloqueo, solo necesita calcular el síndrome$p(b)\text{,}$ y agregar a$b$ la corrección de errores que coincida$p(b)\text{.}$

Concluiremos este ejemplo calculando la probabilidad de éxito para nuestra hipotética situación. Es$\left(0.999^6 + 6 \cdot 0.999^5 \cdot 0.001\right)^{1000}=0.985151\text{.}$ La tarifa para este código es$\frac{1}{2}\text{.}$

Ejemplo$\PageIndex{1}$: Another Linear Code

Considere el código lineal con matriz generadora

\ begin {ecuation*} G =\ left (\ begin {array} {ccccc} 1 & 1 & 0 & 0 & 0\\ 0 & 1 & 1 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1\\ end {array}\ right). \ end {ecuación*}

Dado que$G$ es$3 \times 5\text{,}$ este código codifica tres bits en cinco bits. La pregunta natural que hay que hacer es ¿qué detección o corrección ofrece? Podemos responder a esta pregunta construyendo la matriz de verificación de paridad. Observamos que si$\vec{b}=(b_1, b_2, b_3)$ la función de codificación es

\ begin {ecuación*} e (\ vec {b}) =\ vec {b} G = (b_1, b_1+b_2, b_2, b_1+b_3, b_3)\ final {ecuación*}

donde la adición es la adición mod 2. Si recibimos cinco bits$(c_1,c_2,c_3,c_4,c_5)$ y no se ha producido ningún error, las dos ecuaciones siguientes serían verdaderas.

\[\begin{align}c_1+c_2+c_3&=0\label{eq:1} \\ c_1+c_4+c_5&=0\label{eq:2}\end{align}\]

Observe que en general, el número de ecuaciones de comprobación de paridad es igual al número de bits adicionales que son añadidos por la función de codificación. Estas ecuaciones son equivalentes a la ecuación de matriz única$(c_1,c_2,c_3,c_4,c_5)H = \vec{0}\text{,}$ donde

\ begin {ecuación*} H =\ left (\ begin {array} {cc} 1 & 1\\ 1 & 0\\ 1 & 0\\ 0 & 1\\ 0 & 1\\\ 0 & 1\\\ end {array}\ derecha)\ end {ecuación*}

De un vistazo, podemos ver que este código no corregirá la mayoría de los errores de un solo bit. Supongamos que$\vec{e}=(e_1,e_2,e_3,e_4,e_5)$ se agrega un error en la transmisión de los cinco bits. Específicamente, supongamos que se agrega 1 (mod 2) en posición$j\text{,}$ donde$1 \leq j\leq 5$ y las demás coordenadas de$\vec{e}$ son 0. Entonces cuando calculamos el síndrome de nuestra transmisión recibida, vemos que

\ begin {ecuación*}\ vec {c} H = (\ vec {b} G +\ vec {e}) H = (\ vec {b} G) H +\ vec {e} H =\ vec {e} H.\ end {ecuación*}

Pero$\vec{e}H$ es la$j^{th}$ fila de$H\text{.}$ Si el síndrome es$(1,1)$ sabemos que el error ocurrió en la posición 1 y podemos corregirlo. Sin embargo, si el error está en cualquier otra posición no podemos precisar su ubicación. Si el síndrome es$(1,0)\text{,}$ entonces el error podría haber ocurrido ya sea en la posición 2 o en la posición 3. Este código detecta todos los errores de un solo bit pero solo corrige una quinta parte de ellos.

Ejercicios

Ejercicio$\PageIndex{1}$

Si se está utilizando el código de detección de errores, ¿cómo actuaría sobre los siguientes bloques recibidos?

$\displaystyle (1, 0, 1, 1)$
$\displaystyle (1, 1, 1, 1)$
$\displaystyle (0, 0, 0, 0)$

Contestar

Error detectado, ya que se recibió un número impar de 1's; pedir retransmisión.
No se detectó ningún error; acepte este bloque.
No se detectó ningún error; acepte este bloque.

Ejercicio$\PageIndex{2}$

Expresar las funciones de codificación y decodificación para el código de detección de errores usando matrices.

Ejercicio$\PageIndex{3}$

Si se está utilizando el código de corrección de errores de esta sección, ¿cómo decodificaría los siguientes bloques? Esperar un error que no se pueda arreglar con uno de estos.

$\displaystyle (1,0,0,0,1,1)$
$\displaystyle (1,0,1,0,1,1)$
$\displaystyle (0,1,1,1,1,0)$
$\displaystyle (0,0,0,1,1,0)$
$\displaystyle (1,0,0,0,0,1)$
$\displaystyle (1,0,0,1,0,0)$

Contestar

Síndrome = El mensaje codificado$(1,0,1)\text{.}$ corregido es$(1,1,0,0,1,1)$ y el mensaje original fue$(1, 1, 0)\text{.}$
Síndrome = El mensaje codificado$(1,1,0)\text{.}$ corregido es$(0,0,1,0,1,1)$ y el mensaje original fue$(0, 0, 1)\text{.}$
Síndrome =$(0,0,0)\text{.}$ Sin error, el mensaje codificado es$(0,1,1,1,1,0)$ y el mensaje original fue$(0, 1, 1)\text{.}$
Síndrome = El mensaje codificado$(1, 1,0)\text{.}$ corregido es$(1,0,0,1,1,0)$ y el mensaje original fue$(1, 0, 0)\text{.}$
Síndrome =$(1,1,1)\text{.}$ Este síndrome ocurre sólo si se han conmutado dos bits. No es posible una corrección confiable.
Síndrome = El mensaje codificado$(0,1,0)\text{.}$ corregido es$(1,0,0,1,1,0)$ y el mensaje original fue$(1, 0, 0)\text{.}$

Ejercicio$\PageIndex{5}$

Considere el código lineal definido por la matriz generadora

\ begin {ecuación*} G=\ left (\ begin {array} {cccc} 1 & 0 & 1 & 0\\ 0 & 1 & 1 & 1 & 1\\ end {array}\ derecha)\ end {ecuación*}

¿Qué tamaño de bloques codifica este código y cuál es la longitud de las palabras de código?
¿Cuáles son las palabras clave para este código?
Con este código, ¿se pueden detectar errores de un solo bit? ¿Se pueden corregir todos, algunos o ninguno de los errores de un solo bit?

Contestar: Dejar$G$ ser la$9 \times 10$ matriz obtenida al aumentar la$9\times 9$. La función$e:\mathbb{Z}_2{}^9\to \mathbb{Z}_2{}^{10}$ definida por nos$e(a) = a G$ permitirá detectar errores únicos, ya que siempre$e(a)$ tendrá un número par de unos.

Ejercicio$\PageIndex{6}$: Rectangular Codes

Para construir un código rectangular, particiona su mensaje en bloques de longitud$m$ y luego factoriza$k_1\cdot k_2$ y$m$ coloca los bits en una matriz$k_1 \times k_2$ rectangular como en la siguiente figura. Luego agregas bits de paridad a lo largo del lado derecho y la parte inferior de las filas y columnas. A continuación, la palabra clave se lee fila por fila.

\ begin {ecuation*}\ begin {array} {cccccc}\ blacksquare &\ blacksquare &\ blacksquare &\ cdots &\ blacksquare &\ blacksquare &\ blacksquare &\ blacksquare &\ blacksquare &\ cdots &\ blacksquare &\ square\\ vdots &\ vdots &\ vdots &\ vdots &\ vdots &\ vdots\\ blacksquare &\ blacksquare &\ blacksquare &\ cdots &\ blacksquare &\ square\\ square &\ square &\ square &\ square &\ cdots &\ square &\ square &\\ square &\\ square &\ cdots &\ square &\ square &\ cdots &\ square &\ cdots &\ square &\ cdots &\ square &\ cdots &\\ square &\ cdots &\ square &\ cdots &\ square &\ cdots &\ square &\ cdots &\ square &\ cdots &\ square textrm {bit}\\\ final { array}\ end {ecuación*}

Por ejemplo, si$m$ es 4, entonces nuestra única opción es una matriz de 2 por 2. El mensaje 1101 se codificaría como

\ begin {ecuación*}\ begin {array} {cc|c} 1 & 1 & 0\\ 0 & 1 & 1\\\ hline 1 & 0 &\\\ end {array}\ end {ecuación*}

y la palabra clave es la cadena 11001110.

Supongamos que le enviaron mensajes de cuatro bits usando este código y recibió las siguientes cadenas. ¿Cuáles fueron los mensajes, suponiendo no más de un error en la transmisión de datos codificados?
1. 11011000
2. 01110010
3. 10001111
Si codificaste$n^2$ bits de esta manera, ¿cuál sería la tasa del código?
Los códigos rectangulares son códigos lineales. Para el código rectangular 3 por 2, ¿cuáles son las matrices generadoras y de comprobación de paridad?

Ejercicio$\PageIndex{7}$

Supongamos que el código en Ejemplo$\PageIndex{1}$ se expande para agregar la columna

\ begin {ecuación*}\ left (\ begin {array} {c} 0\\ 1\\ 1\\ end {array}\ derecha)\ end {ecuación*}

a la matriz generadora$G\text{,}$ ¿se pueden corregir todos los errores de un solo bit? Explica tu respuesta.

Contestar

Sí, puede corregir todos los errores de un solo bit porque la matriz de verificación de paridad para el código expandido es

\ begin {ecuación*}
H =\ left (\ begin {array} {ccc}
1 & 1 & 0\\
1 & 0 & 0\\
1 & 0 & 1\\
0 & 1\\ 0 & 1 &
0\\ 0 & 1\\
0 & 0 & 1\\
\ end {array}\ right).
\ end {ecuación*}

Dado que cada posible síndrome de errores de un solo bit es único podemos corregir cualquier error.