1.3: Análisis lógico

Ahora dejaremos atrás el idioma inglés y nos concentraremos en declaraciones lógicas consistentes únicamente en variables y conectivos. Tenga en cuenta que las variables no se limitan a representar declaraciones simples; también pueden representar declaraciones compuestas.

Definición: Valor de la Verdad

la propiedad de ser verdadera o falsa

Dada una declaración lógica, ver las variables como entradas y el valor de verdad de toda la sentencia como una salida. Nos gustaría una manera sistemática de determinar cómo cambia el valor de verdad de la salida a medida que variamos los valores de verdad de las entradas.

Definición: Análisis lógico

el proceso de determinar el valor de verdad de una declaración basada en los valores de verdad de sus subestados variables

Definición: Tabla de la Verdad

método tabular de realización de análisis lógico

Si una sentencia involucra un número finito de variables, entonces como cada variable puede tener uno de solo dos posibles valores de verdad, hay un número finito de diferentes combinaciones de valores de verdad de entrada para la sentencia. Así podemos probar cada combinación una tras otra para determinar todas las salidas posibles. Organizar este análisis en una tabla con todas las posibilidades para las variables de entrada a la izquierda y las salidas resultantes a la derecha.

Nota\(\PageIndex{1}\)

De hecho, si hay\(n\) variables, entonces hay exactamente\(2^n\) diferentes combinaciones de valores de verdad para las variables.

Primero, establezcamos las tablas de verdad de las conectivas básicas (es decir, de declaraciones que contienen exactamente una conectiva).

Figura\(\PageIndex{1}\): Las tablas de verdad de los Cinco Conectivos Básicos.

Nota\(\PageIndex{2}\)

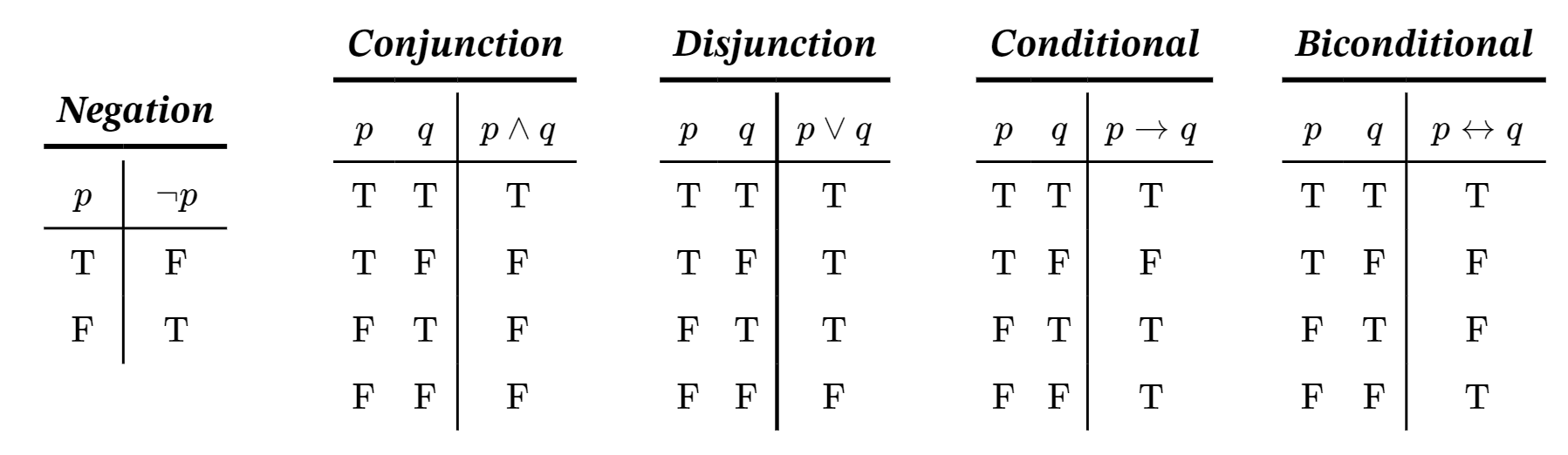
1. \(p \land q\)La conjunción es verdadera sólo cuando ambas\(p\) y\(q\) son verdaderas.
2. \(p \lor q\)La disyunción es cierta cuando al menos uno de\(p\) y\(q\) es cierto.
3. Las dos primeras filas de la tabla de verdad para\(p \rightarrow q\) son consistentes con la lectura “si\(p\) es verdad entonces también\(q\) es verdad”. Realmente, esta lectura del condicional no dice nada en el caso que en realidad\(p\) sea falso, pero no podemos dejar en blanco la columna “output” de la tabla de verdad para las filas correspondientes donde en\(p = F\text{.}\) cambio, las salidas en las dos últimas filas de la tabla de verdad para\(p \rightarrow q\) son “default ” valores elegidos para evitar inconsistencias. (Ver Ejercicio 1.6.3.)
4. Mirando las cuatro filas de la tabla de la verdad porque\(p \rightarrow q\text{,}\) podemos decir sucintamente que\(p \rightarrow q\) es verdad excepto cuando\(p\) es verdad pero\(q\) es falso.
5. Las\(p \leftrightarrow q\) lecturas bicondicionales “\(p\)es verdad cuando\(q\) es verdad, y sólo cuando\(q\) es verdad”. Pero esto quiere decir que cuando\(q\) es falso,\(p\) no puede ser verdad, de ahí debe por falso, lo que explica la cuarta fila de la tabla de la verdad.
6. Mirando las cuatro filas de la tabla de la verdad\(p \leftrightarrow q\text{,}\) porque podemos decir sucintamente que\(p \leftrightarrow q\) es cierto cuando\(p\) y\(q\) tener el mismo valor de verdad.

Ver

Estado 2 de Observación 1.1.1 para la diferencia entre inclusivo o y exclusivo o.

Ahora podemos usar las tablas de verdad de las conectivas básicas para analizar afirmaciones más complicadas. El uso liberal de columnas extra “intermedias” para analizar subsentencias por separado es muy recomendable.

Ejemplo\(\PageIndex{1}\)

Analizar\(\neg (p \leftrightarrow q)\text{.}\)

Solución

\(p\)	\(q\)	\(p \leftrightarrow q\)	\(\neg (p \leftrightarrow q)\)
\(T\)	\(T\)	\(T\)	\(F\)
\(T\)	\(F\)	\(F\)	\(T\)
\(F\)	\(T\)	\(F\)	\(T\)
\(F\)	\(F\)	\(T\)	\(F\)

Nota\(\PageIndex{2}\)

La afirmación lógica\(\neg (p \leftrightarrow q)\) analizada en Ejemplo Trabajado\(\PageIndex{1}\) es una forma de realizar exclusividad o:\(p\) o\(q\) pero no ambas.

Ejemplo\(\PageIndex{2}\)

Analizar\((p \land q) \rightarrow (p \leftrightarrow r)\text{.}\)

Solución

\(p\)	\(q\)	\(r\)	\(p \land q\)	\(p \leftrightarrow r\)	\((p \land q) \rightarrow (p \leftrightarrow r)\)
\(T\)	\(T\)	\(T\)	\(T\)	\(T\)	\(T\)
\(T\)	\(T\)	\(F\)	\(T\)	\(F\)	\(F\)
\(T\)	\(F\)	\(T\)	\(F\)	\(T\)	\(T\)
\(T\)	\(F\)	\(F\)	\(F\)	\(F\)	\(T\)
\(F\)	\(T\)	\(T\)	\(F\)	\(F\)	\(T\)
\(F\)	\(T\)	\(F\)	\(F\)	\(T\)	\(T\)
\(F\)	\(F\)	\(T\)	\(F\)	\(F\)	\(T\)
\(F\)	\(F\)	\(F\)	\(F\)	\(T\)	\(T\)

Ejemplo\(\PageIndex{3}\)

Analizar\(((p\rightarrow q) \rightarrow r \leftrightarrow (p \rightarrow (q \rightarrow r)\text{.}\)

Solución

\(p\)	\(q\)	\(r\)	\(p \rightarrow q\)	\(q \rightarrow r\)	\(A\)	\(B\)	\(A \leftrightarrow B\)
\(T\)	\(T\)	\(T\)	\(T\)	\(T\)	\(T\)	\(T\)	\(T\)
\(T\)	\(T\)	\(F\)	\(T\)	\(F\)	\(F\)	\(F\)	\(T\)
\(T\)	\(F\)	\(T\)	\(F\)	\(T\)	\(T\)	\(T\)	\(T\)
\(T\)	\(F\)	\(F\)	\(F\)	\(T\)	\(T\)	\(T\)	\(T\)
\(F\)	\(T\)	\(T\)	\(T\)	\(T\)	\(T\)	\(T\)	\(T\)
\(F\)	\(T\)	\(F\)	\(T\)	\(F\)	\(F\)	\(T\)	\(F\)
\(F\)	\(F\)	\(T\)	\(T\)	\(T\)	\(T\)	\(T\)	\(T\)
\(F\)	\(F\)	\(F\)	\(T\)	\(T\)	\(F\)	\(T\)	\(F\)