4.2: Manipulación de declaraciones cuantificadas

4.2.1 Negación de declaraciones cuantificadas

Negar declaraciones cuantificadas en inglés puede ser complicado, pero estableceremos reglas que lo faciliten en la lógica simbólica.

Advertencia\(\PageIndex{1}\)

La negación de la afirmación “todos X son Y” no es “no X son Y” ni “todos X no son Y”.

Ejemplo\(\PageIndex{1}\)

¿Cuál es la negación de la afirmación “todas las vacas comen pasto”? Para evitar cometer el error en la advertencia anterior, considere la siguiente pregunta: ¿cuál es el número mínimo de vacas que no comen pasto que se puede utilizar como evidencia para demostrar que la afirmación “todas las vacas comen pasto” es falsa?

Figura\(\PageIndex{1}\): En este caso, tanto “todas las vacas comen pasto” como “algunas vacas comen pasto” son ciertas.

Figura\(\PageIndex{2}\): En este caso, tanto “algunas vacas comen pasto” como “algunas vacas no comen pasto” son ciertas.

Figura\(\PageIndex{3}\): En este caso, cada una de “ninguna vaca come pasto”, “todas las vacas no comen pasto”, y “algunas vacas no comen pasto” son ciertas.

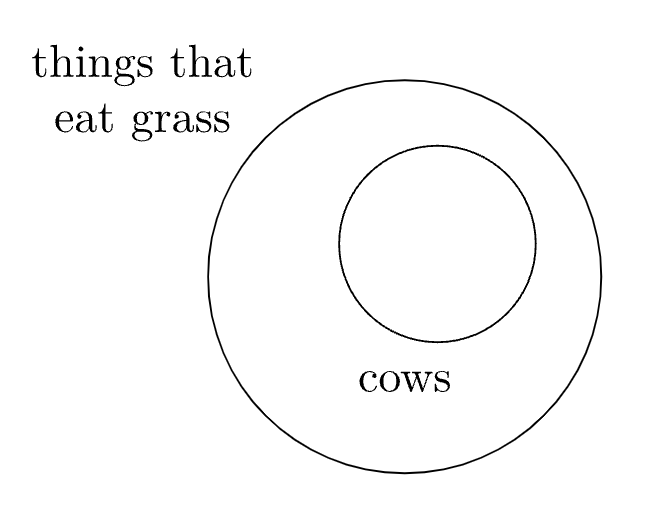
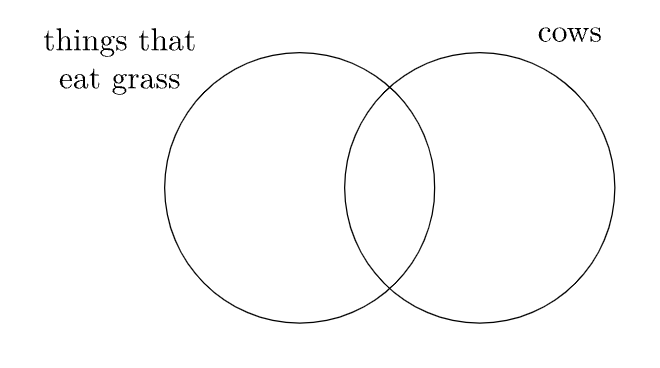
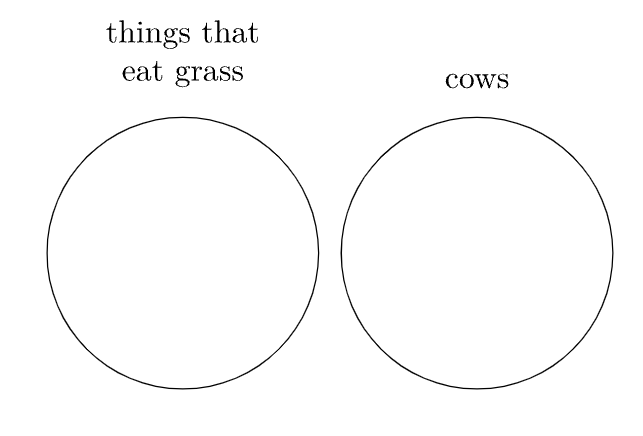
Solo se necesita una vaca devoradora de lasaña para hacer falsa “todas las vacas comen pasto”, por lo que la negación de “todas las vacas comen pasto” es “algunas vacas no comen pasto” o “al menos una vaca no come pasto”.

Advertencia\(\PageIndex{2}\)

Hemos indicado que la afirmación “algunas vacas comen pasto” es técnicamente cierta en el primer diagrama del Ejemplo\(\PageIndex{1}\), aunque es más preciso decir “todas las vacas comen pasto” en esa situación. De igual manera, hemos indicado que la afirmación “algunas vacas no comen pasto” es técnicamente cierta en el tercer diagrama. Recuerda que la verdad y la falsedad suelen ser toda esa materia en lógica, no necesariamente haciendo posible la afirmación más precisa.

Proposición\(\PageIndex{1}\): Rules for negation of quantifiers

Let\(A(x)\) representar un predicado en la variable\(x\text{.}\)

1. Negación universal.

La negación de\((\forall x)A(x)\) es\((\exists x)(\neg A(x))\text{.}\)

2. Negación existencial.

La negación de\((\exists x)A(x)\) es\((\forall x)(\neg A(x))\text{.}\)

Comprueba tu comprensión.

Usa los diagramas de “vacas comen pasto” en Ejemplo\(\PageIndex{1}\) para convencerte de que estas reglas de negación son correctas.

Ejemplo\(\PageIndex{2}\): Negating a quantified statement

Determinar y “simplificar” la negación de

\ begin {ecuación*} (\ forall x)\ left (A (x)\ rightarrow\ {(\ existe y) (\ forall z)\ {B (y)\ land\ neg C (z)\}\}\ right)\ text {.} \ end {ecuación*}

Solución

Usando las reglas de negación del cuantificador y equivalencias lógicas conocidas, podemos realizar las siguientes manipulaciones:

\ begin {alinear*} &\ neg (\ forall x)\ {A (x)\ fila derecha (\ existe y) (\ forall z)\ {B (y)\ tierra\ neg C (z)\}\}\\ &\ Izquierda (\ existe x)\ neg\ {A (x)\ derecha (\ existe y) (\ para todo z)\ {B (y)\ tierra\ neg C (z)\}\} & &\ texto {(i)}\\ &\ Leftrightarrow (\ existe x)\ neg\ {\ neg A (x)\ lor (\ existe y) (\ forall z)\ {B (y)\ tierra\ neg C (z)\}\} &\ texto {(ii)}\\ &\ Leftrightarrow (\ existe x)\ {A (x)\ tierra\ neg (\ existe y) (\ forall z)\ {B (y)\ tierra\ neg C (z)\}\} &\ texto {(iii))}\\ &\ Leftrightarrow (\ existe x)\ {A (x)\ tierra (\ forall y)\ neg (\ forall z)\ {B (y)\ tierra\ neg C (z)\}\} & &\ text {(iv)}\\ &\ Leftrightarrow (\ existe x)\ {A (x)\ tierra (\ forall y) (\ existe z)\ neg\ {B (y)\ tierra\ neg C (z)\}\} &\ text {(v)}\\ &\ Izquierda (\ existe x)\ {A (x)\ tierra (\ forall y) (\ existe z)\ {\ neg B (y)\ lor C (z)\}\} &\ text {(vi)}\ end {align*}
con justificaciones

1. negación del cuantificador;
2. equivalencia conocida\(p\rightarrow q \Leftrightarrow \neg p \lor q\text{;}\)
3. DeMorgan, doble negación;
4. negación del cuantificador;
5. negación del cuantificador; y
6. DeMorgan, doble negación.

4.2.2 Distribuir cuantificadores

Proposición\(\PageIndex{2}\): Rules for distributing quantifiers

Let\(A(x),B(x)\) representar predicados en la variable\(x\text{.}\)

1. \(\displaystyle (\forall x)\{A(x) \land B(x)\} \Leftrightarrow (\forall x)A(x) \land (\forall x)B(x)\)
2. \(\displaystyle (\exists x)\{A(x) \lor B(x)\} \Leftrightarrow (\exists x)A(x) \lor (\exists x)B(x)\)

Ejemplo\(\PageIndex{3}\)

• La afirmación “cada verdura es deliciosa y nutritiva” es lo mismo que decir “cada verdura es deliciosa y cada verdura es nutritiva”.
• El enunciado “al menos una verdura en el huerto está podrida o mordisqueada por ardillas” es lo mismo que decir “al menos una verdura en el huerto está podrida o al menos una verdura en el huerto es mordisqueada por ardillas”.

Advertencia\(\PageIndex{3}\)

• El cuantificador universal\(\forall\) no distribuye sobre disyunción\(\lor\text{.}\)
• El cuantificador existencial\(\exists\) no distribuye sobre conjunción\(\land\text{.}\)

Comprueba tu comprensión.

1. Crear un ejemplo de predicados\(A(x)\) y\(B(x)\) tal que, de los enunciados

   \ begin {alinear*} (\ forall x) &\ {A (x)\ or B (x)\}\ text {,} & (\ para todos x) A (x) &\ lor (\ para todos x) B (x)\ texto {,}\ end {alinear*}

   el primero es cierto pero el segundo es falso.
2. Crear un ejemplo de predicados\(A(x)\) y\(B(x)\) tal que, de los enunciados

   \ begin {align*} (\ existe x) &\ {A (x)\ tierra B (x)\}\ texto {,} & (\ existe x) A (x) &\ tierra (\ existe x) B (x)\ texto {,}\ end {alinear*}

   el primero es falso pero el segundo es cierto.