9.3: Subconjuntos e igualdad de conjuntos
- Page ID
- 118201
A menudo queremos distinguir una colección de ciertos elementos “especiales” dentro de un conjunto más amplio de elementos.
un conjunto cuyos elementos son todos miembros de otro conjunto
set\(A\) es un subconjunto de o está contenido en conjunto\(B\)
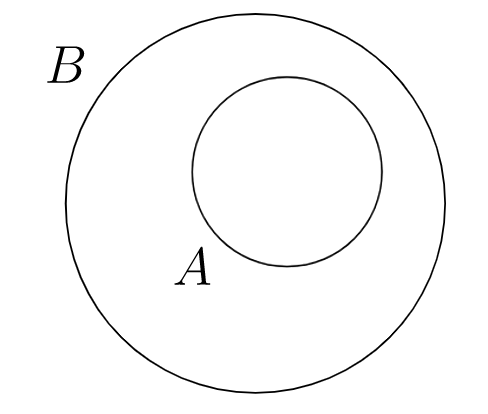
También a veces usamos la frase “contenida en” para significar que un objeto es un elemento de un conjunto.
Para demostrar\(A\subseteq B\text{,}\) demostrar\((\forall x)(x \in A \rightarrow x \in B)\text{.}\)
- Cada número natural es un entero, así que\(\mathbb{N} \subseteq \mathbb{Z}\text{.}\) Para enfatizar esto, podríamos escribir\(\mathbb{N} = \{m \in \mathbb{Z} \vert m \ge 0 \}\text{.}\)
- Cada entero puede considerarse como un número racional, ya que para cada uno\(m\in\mathbb{Z}\) podemos escribir\(m = \dfrac{a}{b}\) con\(a=m\) y\(b=1\text{.}\) Así\(\mathbb{Z} \subseteq \mathbb{Q}\text{.}\)
- Cada número racional puede considerarse un número real si identificamos fracciones con sus expansiones decimales a través de división larga. Por lo tanto\(\mathbb{Q} \subseteq \mathbb{R}\text{.}\)
Cuando definimos un conjunto por notación de condición candidata, primero especificamos un conjunto de elementos candidatos, y luego una condición o colección de condiciones que esos candidatos deben cumplir para poder ser incluidos realmente en el conjunto. Pero entonces cada elemento del conjunto que estamos definiendo debe ser primero del conjunto de elementos candidatos, por lo que nuestro conjunto definido debe ser un subconjunto del conjunto candidato.
Por ejemplo, en Ejemplo\(\PageIndex{1}\), proporcionamos una definición para el conjunto\(\mathbb{N}\) en forma de candidato-condición donde el grupo de candidatos es el conjunto\(\mathbb{Z}\text{.}\) Esta definición hace explícito que\(\mathbb{N} \subseteq \mathbb{Z}\text{.}\)
Demostrar que\(A \subseteq B\) para
\ begin {alinear*} A & =\ {3m + 1\ vert m\ in\ mathbb {Z}\}, & B & =\ izquierda\ {x\ in\ mathbb {R}\ bigg\ vert\ sin\ izquierda (\ dfrac {\ pi (x-1)} {3}\ derecha) = 0\ derecha\}. \ end {alinear*}
Solución
Hay un número infinito de elementos de\(A\text{,}\) por lo que no podemos comprobar que todos los elementos de\(A\) son también elementos de\(B\) uno por uno. En cambio, dejamos que una variable\(x\) represente un elemento arbitrario pero no especificado de\(A\text{.}\) Dado que todos los elementos de\(A\) tienen la forma\(3m+1\) para algunos\(m \in \mathbb{Z}\text{,}\) tenemos\(x = 3m+1\) para algunos\(m \in \mathbb{Z}\text{.}\) Comprobar la condición para ser un elemento de\(B\) calculando
\ begin {ecuación*}\ sin\ izquierda (\ dfrac {\ pi (x-1)} {3}\ derecha) =\ sin\ izquierda (\ dfrac {\ pi ((3m+1) -1)} {3}\ derecha) =\ sin (m\ pi) = 0. \ end {ecuación*}
Por lo tanto,\(x \in B\text{.}\) ya que el cálculo anterior funciona para cada\(m \in \mathbb{Z}\text{,}\) todos los elementos de\(A\) son elementos de\(B\text{.}\)
- Cada conjunto tiene un conjunto vacío como subconjunto. Es decir, siempre\(\emptyset \subseteq S\) es cierto para un conjunto\(S\text{.}\)
- Cada conjunto es un subconjunto de sí mismo. Es decir, siempre\(S \subseteq S\) es cierto para un conjunto\(S\text{.}\)
- La relación de subconjunto es transitiva. Es decir, cuando\(A \subseteq B\) y\(B \subseteq C\) son ciertos, entonces también\(A \subseteq C\) es cierto.
Una mirada hacia adelante. Estudiaremos las nociones abstractas de relación y la propiedad transitiva en el Capítulo 17.
escribir\(A = B\) si ambos conjuntos constan precisamente de los mismos elementos
Para demostrar\(A = B\text{,}\) comprobar que ambos\(A \subseteq B\) y\(B \subseteq A\text{.}\)
Esto requiere dos aplicaciones de la prueba de subconjunto:
- comenzar con el supuesto\(x \in A\) y proceder a la conclusión\(x \in B\text{;}\)
- comenzar con el supuesto\(x \in B\) y proceder a la conclusión\(x \in A\text{.}\)
Se podrían combinar ambas aplicaciones de la Prueba de Subconjuntos descrita en la Prueba de Igualdad de Conjunto anterior en una bicondicional:\(A = B\) es verdadera si
\ begin {ecuación*} (\ forall x) (x\ in A\ Leftrightarrow x\ in B)\ end {ecuación*}
es verdad. Si la lógica de\(x \in A \rightarrow x \in B\) se invierte fácilmente, entonces tiene sentido argumentar\(x \in A \Leftrightarrow x \in B\) en lugar de argumentar por separado\(x \in A \rightarrow x \in B\) y\(x \in B \rightarrow x \in A\text{.}\) Sin embargo, en la mayoría de los casos se prefieren argumentos separados de estas implicaciones lógicas.
Dejar\(A\) y\(B\) ser como en Ejemplo Trabajado\(\PageIndex{3}\). Demostrar que\(A = B\text{.}\)
Solución
Espectáculo\(A\subseteq B\). Ver Ejemplo Trabajado\(\PageIndex{3}\).
Espectáculo\(B \subseteq A\). Dejar\(x\) representar un elemento arbitrario de\(B\text{.}\) Esto significa que
\ begin {ecuación*}\ sin\ izquierda (\ dfrac {\ pi (x-1)} {3}\ derecha) = 0. \ end {ecuación*}
Sin embargo, sabemos por trigonometría que\(\sin \theta = 0\) si y solo si\(\theta\) es un múltiplo entero de\(\pi\text{;}\) es decir,\(\theta = m\pi\) para algunos\(m \in \mathbb{Z}\text{.}\) Si establecemos
\ begin {ecuación*}\ dfrac {\ pi (x-1)} {3} = m\ pi\ final {ecuación*}
y resolvemos para\(x\text{,}\) que obtengamos\(x = 3m+1 \in A\text{.}\)
un conjunto contenido pero no igual a otro conjunto
set\(A\) es un subconjunto apropiado de conjunto\(B\)
Algunas personas excluyen\(\emptyset\) de la definición de subconjunto propio.
Test\(\PageIndex{3}\): For a proper subset
Demostrar\(A \subsetneqq B\text{,}\) primera prueba\(A \subseteq B\) como de costumbre (Prueba\(\PageIndex{1}\), pero también demostrar que existe alguna\(x \in B\) tal que\(x \notin A\text{.}\)
Ya lo sabemos\(\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \subseteq \mathbb{R}\text{,}\) pero tenemos
- \(\mathbb{N} \subsetneqq \mathbb{Z}\text{,}\)ya que, por ejemplo,\(-1 \in \mathbb{Z}\) pero\(-1 \notin \mathbb{N}\text{;}\)
- \(\mathbb{Z} \subsetneqq \mathbb{Q}\text{,}\)ya que, por ejemplo,\(\dfrac{1}{2} \in \mathbb{Q}\) pero\(\dfrac{1}{2} \notin \mathbb{Z}\text{;}\) y
- \(\mathbb{Q} \subsetneqq \mathbb{R}\text{,}\)ya que, por ejemplo,\(\sqrt{2} \in \mathbb{R}\) pero\(\sqrt{2} \notin \mathbb{Q}\text{.}\)
Para mostrar la\(A \neq B\) parte de\(A\subsetneqq B\text{,}\) usted solo necesita exhibir un elemento de ejemplo del\(B\) cual no está en\(A\text{;}\), es decir, necesita encontrar un contraejemplo para la implicación lógica\(x \in B \rightarrow x \in A\text{.}\)


