9.4: Complemento, unión e intersección

En primer lugar, suele ser conveniente restringir el alcance de la discusión.

Definición: Universal set

un conjunto que contiene todos los objetos actualmente en consideración

Consideraremos que todas las siguientes operaciones de conjunto se realizarán dentro de un conjunto universal\(U\text{.}\) En particular, supongamos\(A,B\subseteq U\text{.}\)

9.4.1: Complemento universal y relativo

Definición: Complemento

el conjunto de elementos de los\(U\) cuales no están en\(A\)

Definición:\(A^{C}\)

el complemento de\(A\) (in\(U\)), de manera que

\ comenzar {ecuación*} A^ {C} =\ {x\ en U\ vert x\ notin A\}\ final {ecuación*}

Definición: Complemento relativo

si\(A,B \subseteq U\text{,}\) el complemento de\(A\) in\(B\) es el conjunto de elementos de los\(B\) cuales no están en\(A\)

Definición:\(B \setminus A\)

el complemento de\(A\) en\(B\text{,}\) para que

\ begin {ecuación*} B\ setmenos A =\ {x\ in B\ vert x\ notin A\}\ final {ecuación*}

Figura\(\PageIndex{1}\): Diagramas de Venn de complementos conjuntos universales y relativos.

 

 

Nota\(\PageIndex{1}\)

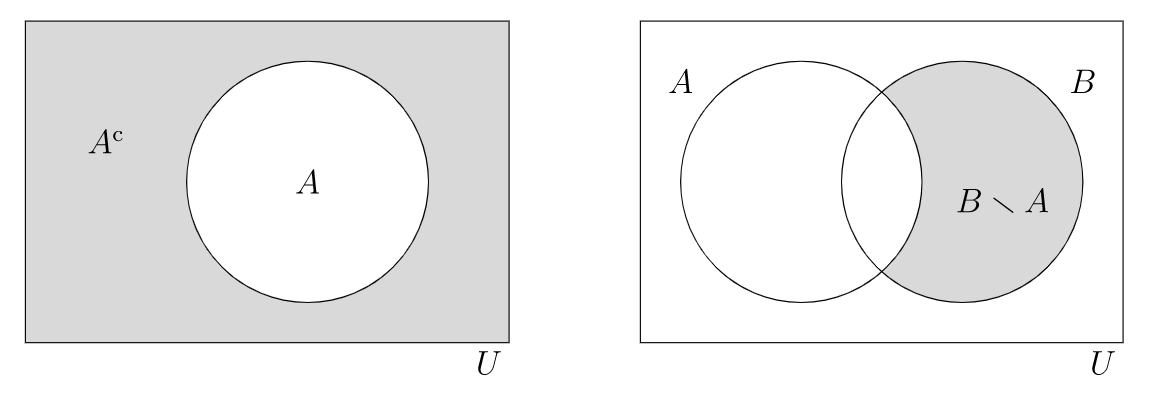
Otra notación común para el complemento relativo es\(B - A\text{.}\) Sin embargo, esta entra en conflicto con la notación para la operación algebraica de resta en ciertos contextos, por lo que preferiremos la notación\(B \setminus A\text{.}\)

Ejemplo\(\PageIndex{1}\): Some examples of relative complement involving number sets

• Supongamos\(B = \{ 1, 2, 3, 4, 5, 6 \}\) y\(A = \{ 1, 3, 5 \}\text{.}\) Entonces\(B \setminus A = \{ 2, 4, 6 \}\text{.}\)
• El complemento del conjunto de números racionales\(\mathbb{Q}\) dentro del conjunto de números reales\(\mathbb{R}\) se llama el conjunto de números irracionales, y escribimos\(\mathbb{I} = \mathbb{R} \setminus \mathbb{Q} \) para este conjunto. Si estás pensando en números reales en términos de sus expansiones decimales, los números irracionales son precisamente aquellos que tienen expansiones decimales no terminantes, no repetidas.

9.4.2: Conjuntos de unión, intersección y disjuntos

Definición: Unión

la colección combinada de todos los elementos en un par de conjuntos

Definición:\(A \cup B\)

la unión de conjuntos\(A\) y\(B\text{,}\) para que

\ comenzar {ecuación*} A\ copa B =\ {x\ en U\ vert x\ en A\ texto {o} x\ en B\ texto {(o ambos)}\}\ final {ecuación*}

Definición: Intersección

la colección de solo aquellos elementos comunes a un par de conjuntos

Definición:\(A \cap B\)

la intersección de\(A\) y\(B\text{,}\) para que

\ comenzar {ecuación*} A\ cap B =\ {x\ en U\ vert x\ en A\ texto {y} x\ en B\}\ final {ecuación*}

Figura\(\PageIndex{1}\): Diagramas de Venn de unión e intersección de conjuntos.

Nota\(\PageIndex{2}\)

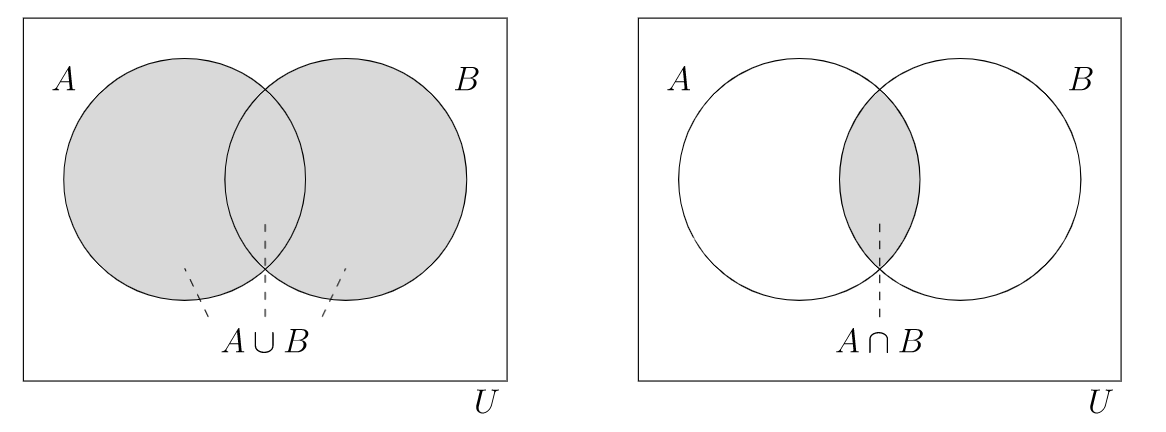
Una unión contiene cada elemento de ambos conjuntos, por lo que contiene ambos conjuntos como subconjuntos:

\ comenzar {ecuación*} A, B\ subseteq A\ copa B\ texto {.} \ end {ecuación*}

Por otro lado, cada elemento en una intersección está en ambos conjuntos, por lo que la intersección es un subconjunto de ambos conjuntos:

\ begin {ecuación*} A\ cap B\ subseteq A, B\ texto {.} \ end {ecuación*}

Ejemplo\(\PageIndex{2}\)

Para subconjuntos\(A = \{1,2,3,4\}\) y\(B = \{3,4,5,6\}\) de\(\mathbb{N}\text{,}\) tenemos

\ begin {alinear*} A\ copa B & =\ {1,2,3,4,5,6\}, & A\ cap B & =\ {3,4\}. \ end {align*}

Ejemplo\(\PageIndex{3}\)

Considere los siguientes subconjuntos de\(\mathbb{N}\text{.}\)

\ begin {align*}\ scr {E} & =\ {n\ in\ mathbb {N}\ vert n\ text {par}\} &\ scr {P} & =\ {n\ in\ mathbb {N}\ vert n\ text {prime,} n\ mathbb {N} e 0\}\\\ scr {O} & =\ {n\ en\ mathbb N}\ vert n\ texto {impar}\} &\ scr {T} & =\ {3n\ vert n\ in\ mathbb {N}\} =\ {0,\, 3,\, 6,\, 9,\,\ ldots\}\ end {align*}
Entonces,

\ begin {align*}\ scr {E}\ copa\ scr {O} & =\ mathbb {N}, &\ scr {E}\ cap\ scr {P} & =\ {2\}, &\ scr {E}\ cap\ scr {T} & =\ {6n\ vert n\ in\ mathbb {N}\},\\ scr {E}\ cap\ scr {O} & =\ emptyset, &\ scr {O}\ cap\ scr {P} & =\ scr {P}\ setmenos\ {2\}, &\ scr {O}\ cap\ scr {T} & =\ {6n+3\ vert n \ in\ mathbb {N}\}. \ end {align*}

Definición: Conjuntos Disjoint

conjuntos que no tienen elementos en común, es decir, conjuntos\(A,B\) tales que\(A\cap B = \emptyset\)

Definición: Unión Disjoint

una unión\(A \cup B\) donde\(A\) y\(B\) son disjuntas

Definición:\(A \sqcup B\)

la unión disjunta de conjuntos\(A\) y\(B\)

Figura\(\PageIndex{2}\): Diagrama de Venn de una unión de conjunto disjunta.

Ejemplo\(\PageIndex{4}\)

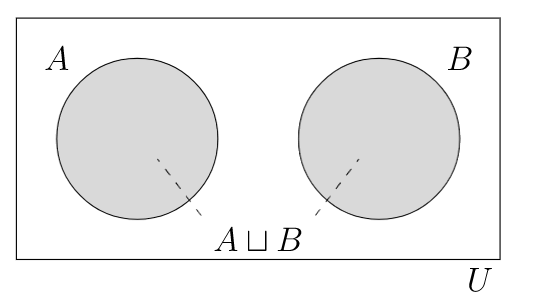
Los conjuntos\(\scr{E},\scr{O}\) de Ejemplo\(\PageIndex{3}\) son disjuntos, y\(\mathbb{N} = \scr{E} \sqcup \scr{O}\text{.}\)

Observación\(\PageIndex{1}\)

Si\(A \subseteq U\text{,}\) entonces podemos expresarnos\(U\) como una unión disjunta\(U = A \sqcup A^{C}\text{.}\) Del mismo modo, si\(U = A \sqcup B\text{,}\) entonces debemos tener\(B = A^{C}\text{.}\)

9.4.3: Reglas para operaciones de conjunto

Proposición\(\PageIndex{1}\): Rules for Operations on Sets

Supongamos que\(A,B,C\) son subconjuntos de un conjunto universal\(U\text{.}\) Entonces se mantienen las siguientes igualdades del conjunto.

1. Propiedades del conjunto universal.
   1. \(\displaystyle A \cup U = U \)
   2. \(\displaystyle A \cap U = A \)
2. Propiedades del conjunto vacío.
   1. \(\displaystyle A \cup \emptyset = A \)
   2. \(\displaystyle A \cap \emptyset = \emptyset \)
3. Dualidad de conjuntos universales y vacíos.
   1. \(\displaystyle U^{C} = \emptyset \)
   2. \(\displaystyle \emptyset ^{C} = U \)
4. \(\displaystyle (A^{C})^C = A \)
5. Idempotencia.
   1. \(\displaystyle A \cup A = A \)
   2. \(\displaystyle A \cap A = A \)
6. Conmutatividad.
   1. \(\displaystyle A \cup B = B \cup A \)
   2. \(\displaystyle A \cap B = B \cap A \)
7. Asociatividad.
   1. \(\displaystyle (A \cup B) \cup C = A \cup (B \cup C) \)
   2. \(\displaystyle (A \cap B) \cap C = A \cap (B \cap C) \)
8. Distributividad.
   1. \(\displaystyle A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \)
   2. \(\displaystyle A \cup (B \cap C) = (A \cup B) \cap (A \cup C) \)
   3. \(\displaystyle (A \cup B) \cap C = (A \cap C) \cup (B \cap C) \)
   4. \(\displaystyle (A \cap B) \cup C = (A \cup C) \cap (B \cup C) \)
9. Leyes de DeMorgan.
   1. \(\displaystyle (A \cup B)^C = A^{C} \cap B^C \)
   2. \(\displaystyle (A \cap B)^C = A^{C} \cup B^C \)

 

Prueba de Regla 9.a.

Recordemos que para probar esta igualdad establecida, necesitamos mostrar tanto

\ begin {alinear*} (A\ copa B) ^C &\ subseteq A^ {C}\ cap B^C\ text {,} & A^ {C}\ cap B^C &\ subseteq (A\ copa B) ^C\ texto {.} \ end {align*}

Espectáculo\((A \cup B)^C \subseteq A^{C} \cap B^C\).
Tenemos que mostrar

\ begin {ecuación*} x\ in (A\ copa B) ^C\ Rightarrow x\ in A^ {C}\ cap B^C\ text {.} \ end {ecuación*}

Si\(x \in (A \cup B)^C\) entonces por definición de complemento,\(x\in U\) pero\(x \notin A \cup B\text{.}\) Entonces\(x \notin A\) debe ser cierto, ya que si\(x\) estuvieran en\(A\) entonces también estaría en\(A \cup B\text{.}\) De igual manera, también\(x \notin B\) debe ser cierto. Entonces\(x \in A^{C}\) y\(x\in B^C\text{;}\) i.e.\(x\in A^{C} \cap B^C\text{.}\)

Espectáculo\(A^{C} \cap B^C \subseteq (A \cup B)^C \). Tenemos que mostrar

\ begin {ecuación*} x\ in A^ {C}\ cap B^C\ Rightarrow x\ in (A\ copa B) ^C\ text {.} \ end {ecuación*}

Si\(x \in A^{C} \cap B^C\) entonces por definición de intersección, ambos\(x \in A^{C}\) y\(x \in B^C\) son verdaderos.; es decir,\(x \notin A\) y\(x \notin B\text{.}\) Desde\(A \cup B\) es todos los elementos de los\(U\) cuales están en uno (o ambos) de\(A,B\text{,}\) debemos tener\(x \notin A \cup B\text{.}\) Así\(x \in (A \cup B)^C\text{.}\)

Pruebas de las otras reglas.

Estos se dejan a usted, el lector, en el Ejercicio 9.9.1.

 

Observación\(\PageIndex{2}\)

Compare las reglas de operación establecidas de la proposición anterior con las Reglas de Cálculo Proposicional.