10.1: Conceptos básicos
- Page ID
- 118315
10.1.1: Terminología y conceptos básicos
una regla que asigna a cada elemento de entrada de un conjunto\(A\) un único elemento de salida de un conjunto\(B\)
el conjunto de todos los elementos de entrada posibles para una función
un conjunto que contiene todos los elementos de salida posibles para una función
\(f\)es una función con dominio\(A\) y codominio\(B\)
el proceso/algoritmo/regla/fórmula que describe cómo cada elemento de entrada del dominio se transformará en un elemento de salida en el codominio
la función\(f: A \rightarrow B\) asocia el elemento codomain\(b\in B\) al elemento domain\(a\in A\)
notación alternativa para\(f(a) = b\)
cuando\(f(a) = b\) decimos que\(b\) es la imagen de\(a\) debajo\(f\text{,}\) o que\(f\) mapea\(a\) a\(b\)
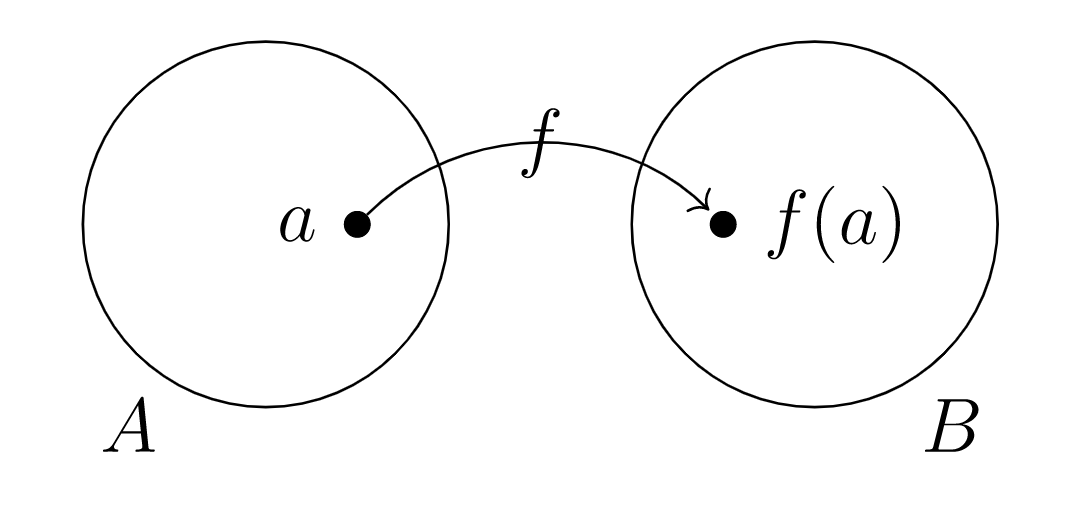
Cuando definimos una función, el dominio debe estar implícitamente claro a partir de la regla de entrada-salida, o explícitamente declarado para que se conozca la colección precisa de elementos de entrada permitidos.
Sin embargo, sería demasiado oneroso hacer lo mismo para la colección precisa de elementos de salida, a menudo cuando creamos una función inicialmente no sabremos exactamente qué salidas producirá. El propósito de declarar un codominio es para que al menos quede claro qué tipo de elemento de salida se produce.
10.1.2: Definición de funciones
Definir una función es un proceso de dos pasos, en el que necesitamos especificar tres piezas de información:
- el dominio,
- el codominio, y
- la regla de entrada-salida.
Los dos primeros datos se especifican en un solo paso, cuando escribimos
Esta notación indica que\(A\) será el dominio y\(B\) será el codominio para la función llamada Por\(f\text{.}\) supuesto, el nombre de la función es una pieza adicional de información que se especifica con esta notación, pero nombrar una función es opcional (aunque muy recomendable!).
La especificación de la regla de entrada-salida se puede hacer de muchas maneras diferentes, por ejemplo, mediante una fórmula, tabla de valores, una descripción de un proceso o algoritmo paso a paso para determinar o calcular una salida dada una entrada arbitraria, etc.
Una fórmula de entrada-salida como\(f(x) = \sqrt{x}\) define una función, pero aquí tenemos que tener cuidado con el dominio. El dominio y el codominio para esta función podrían especificarse como\(f: \mathbb{R}_{\geq 0} \rightarrow \mathbb{R} \text{,}\) donde\(\mathbb{R}_{\geq 0}\) representa el conjunto de números reales no negativos.
En la definición de la función
\ begin {align*} f\ colon\ mathbb {R} &\ to\ mathbb {R},\\ x &\ mapsto\ dfrac {1} {x^2},\ end {align*}
la primera línea de la definición nos dice el dominio (\(\mathbb{R}\)), codominio (de nuevo\(\mathbb{R}\)), y un nombre para la función (\(f\)). La segunda línea nos dice la regla input-output, de modo que
\ begin {ecuación*} f (x) =\ dfrac {1} {x^2}\ texto {.} \ end {equation*}
Sin embargo, en una inspección más cercana descubrimos que el dominio ha sido especificado incorrectamente, ya que no\(x=0\) es una entrada permisible para la regla de entrada y salida. En su lugar, deberíamos escribir
\ begin {ecuación*} f:\ mathbb {R}\ setmenos\ {0\}\ fila derecha\ mathbb {R}\ texto {.} \ end {equation*}
Aunque esta función solo producirá números reales positivos como salidas, el codominio es aceptable como se indica. Sería más preciso escribir
\ begin {ecuation*} f:\ mathbb {R}\ setmenos\ {0\}\ rightarrow\ mathbb {R} _ {>0},\ end {equation*}
donde\(\mathbb{R}_{>0}\) representa el conjunto de números reales positivos, pero no es necesario hacerlo.
Considere la función\(\mathscr{P}(\mathbb{Z}) \to \mathbb{N}\) donde se calculan las salidas de acuerdo con el siguiente algoritmo.
Dado un elemento de entrada\(X \in \mathscr{P}(\mathbb{Z})\) (que, por definición, es un conjunto de enteros), llevar a cabo lo siguiente.
- Calcular el valor absoluto de cada elemento en\(X\text{.}\) (Si\(X\) está vacío, omita este paso.)
- Determinar el resultado mínimo de los cálculos del valor absoluto en el paso anterior. (Si\(X\) está vacío, no habrá ningún resultado de cálculo de valor absoluto para comparar, así que tome\(0\) como el “mininum” en su lugar.)
- Multiplique por el valor mínimo encontrado en el paso anterior\(2\) y sume\(1\text{.}\) Salida de este resultado final.
Sin embargo, con la notación correcta, un algoritmo como el anterior a menudo se puede convertir en una fórmula de entrada-salida — ver Ejemplo 10.4.4.
Para\(\mathscr{N} = \{1,2,3\}\) y\(\mathscr{A} = \{a,b,c,d\}\text{,}\) una forma de definir una función\(f: \mathscr{N}\rightarrow \mathscr{A}\) es
\ begin {align*} f (1) & = d, & f (2) & = a, & f (3) & = d.\ end {align*}
En un primer curso de cálculo, un estudiante normalmente estudia solo funciones de una sola variable, es decir, funciones con una sola variable de entrada y una única variable de salida. En cursos posteriores de cálculo, un estudiante puede estudiar funciones multivariables con múltiples variables de entrada, como
\ begin {ecuación*} f (x, y) = x^2 + y^2\ texto {.} \ end {equation*}
Técnicamente, deberíamos escribir
\ begin {ecuation*} f ((x, y)) = x^2 + y^2\ text {,}\ end {equation*}
como la definición adecuada de\(f\) es\(f: \mathbb{R}^2 \rightarrow \mathbb{R}\text{,}\) pero los corchetes adicionales no transmiten información adicional y solo desordenan las cosas.
Las funciones con múltiples variables de salida reales a menudo se denominan funciones vectoriales. Por ejemplo,\(g: \mathbb{R}\rightarrow\mathbb{R}^2\) definido por
\ begin {ecuation*} g (t) = (t, t^2)\ end {ecuation*}
puede considerarse como una parametrización vectorial de una parábola en el plano.
Y por supuesto también podríamos considerar funciones vectoriales multivariables. Una función\(\varphi: \mathbb{R}^2 \rightarrow \mathbb{R}^2 \) como
\ begin {ecuación*}\ varphi (s, t) = (s-t, s+t)\ end {ecuación*}
podría considerarse como un cambio de variables
\ comenzar {alinear*} x & = s - t, & y & = s + t.\ final {alinear*}
Una declaración lógica\(S\) que involucra variables de declaración\(p_1, p_2, \ldots , p_m\) es esencialmente una función multivariable
\ begin {equation*} S:\ lambda^M\ rightarrow\ Lambda\ text {,}\ end {equation*}
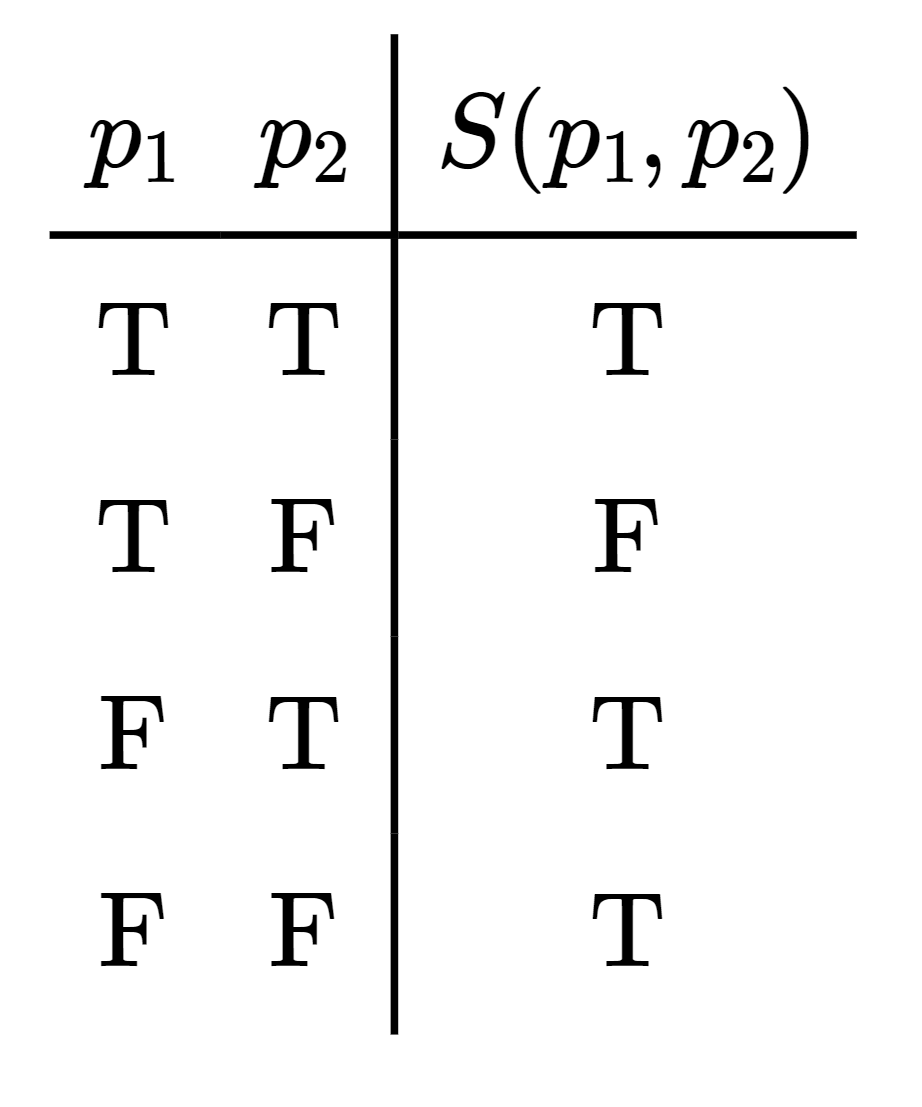
donde\(\Lambda = \{ T,\, F \}\text{.}\) Por ejemplo, la sentencia
\ begin {ecuación*} S (p_1, p_2) = (p_1\ fila derecha p_2)\ end {ecuación*}
es una función\(S: \Lambda \times \Lambda \rightarrow \Lambda \text{,}\) donde
\ begin {alinear*} S (T, T) & = T, & S (T, F) & = F, & S (F, T) & = T, & S (F, F) & = T.\ final {alinear*}
10.1.3: Gráfica de una función
el conjunto de todos los pares de entrada-salida para la función
la gráfica de la función\(f: A \rightarrow B\text{,}\) para que
\ comenzar {ecuación*}\ Delta (f) =\ {(a, f (a))\ vert a\ en A\}\ subseteq A\ veces B\ final {ecuación*}
Para describir la gráfica de la función\(f: \mathscr{N} \rightarrow \mathscr{A}\) definida en Ejemplo\(\PageIndex{4}\), solo necesitamos recopilar los pares de entrada-salida definidos en elementos de producto cartesianos:
Esta gráfica puede representarse de manera más simple por una tabla:
| \(x\) | \(1\) | \(2\) | \(3\) |
| \(f(x)\) | \(d\) | \(a\) | \(d\) |
La gráfica de una función\(f: \mathbb{R} \rightarrow \mathbb{R}\) es un subconjunto de Normalmente\(\mathbb{R} \times \mathbb{R} = \mathbb{R}^2\text{.}\) representamos\(\mathbb{R}^2\) visualmente como el\(xy\) -plano y la gráfica\(\Delta (f) \subseteq \mathbb{R}^2\) como una curva en el plano.
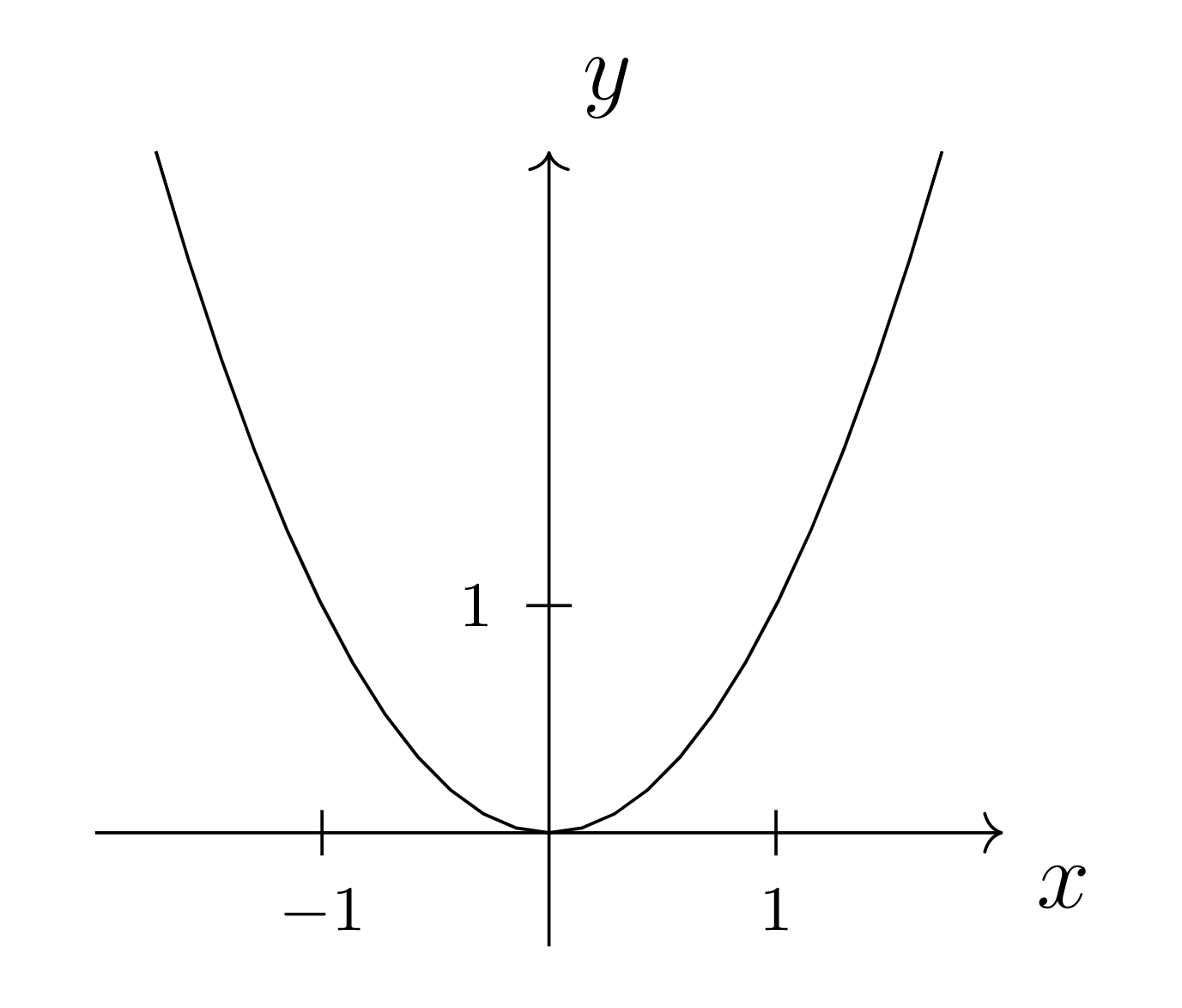
En la gráfica\(f(x) = x^2\) anterior, cada punto de la curva representa un elemento del\(\mathbb{R}^2\) cual está en el subconjunto\(\Delta (f)\text{.}\) Por ejemplo,\((-1,1) \in \Delta (f)\) pero\((-1,\pi) \notin \Delta (f)\text{.}\)
El gráfico de una función\(f: \mathbb{R}^2 \rightarrow \mathbb{R}\) es técnicamente un subconjunto de\(\mathbb{R}^2 \times \mathbb{R}\text{,}\) pero generalmente solo pensamos en esto como\(\mathbb{R}^3\text{,}\) o\(3\) -espacio. En lugar de una curva, tal gráfica define una superficie en\(\mathbb{R}^3\text{.}\) Por ejemplo, el gráfico de la función\(f(x,y) = x^2 + y^2\) de Ejemplo\(\PageIndex{5}\) es un cono parabólico, es decir, una superficie similar a un cono (no sólido) con lados parabólicos.
Ya nos encontramos con la gráfica de una declaración lógica: generalmente se representa como una tabla de verdad. Por ejemplo, la gráfica\(\Delta (S)\) de la sentencia lógica
donde\(\Lambda = \{ T, F \}\) como de costumbre, se puede representar de la siguiente manera.
Desafortunadamente, falta nuestra definición de trabajo para la función: ¿qué es una “regla”? En lugar de perseguir algún círculo de definiciones, podemos llegar a una mejor definición al notar que la gráfica de una función contiene toda la información necesaria sobre la función.
un subconjunto\(F \subseteq A \times B\) tal que para cada uno\(x\in A\) hay exactamente un elemento\((a,b)\in F\) con\(a=x\)
En esta definición formal, estamos definiendo una función para que sea lo que antes habríamos llamado su gráfica.
Ahora estamos definiendo una función\(f: \mathbb{R} \rightarrow \mathbb{R}\) para que sea el subconjunto del plano cartesiano\(\mathbb{R}^2\) que consiste en la gráfica de la función. En este caso, se puede pensar en el requisito de “exactamente uno” como equivalente a la prueba de línea vertical: un valor de entrada no puede producir más de un valor de salida. (Aunque la “una” parte de “exactamente una” captura nuestro requisito de que se defina una función en cada elemento de dominio).
10.1.4: Indefinido y bien definido
Tenemos que tener cuidado definiendo funciones; a veces lo que pensamos que es una función resulta no ser una función.
De nuevo escribir\(\mathscr{N} = \{1,2,3\}\)\(\mathscr{A} = \{a,b,c,d\}\text{,}\) y considerar
\ begin {ecuación*} F =\ {(1, a), (3, d)\}\ subseteq\ mathscr {N}\ veces\ mathscr {A}\ text {.} \ end {equation*}
¿Este subconjunto define una función con dominio\(\mathscr{N}\) y codominio Es\(\mathscr{A}\text{?}\) decir, existe una función\(f: \mathscr{N} \rightarrow \mathscr{A}\) tal que\(F = \Delta (f)\text{?}\) La respuesta es no, porque no hay par entrada-salida adentro\(F\) con el elemento domain\(2\text{.}\) If we intentar considerar una función\(f\) con graph no\(\Delta (f) = F\text{,}\) tenemos forma de decir qué resultado\(f(2)\) debe devolver. En otras palabras, tal\(f\) voluntad se ha dejado indefinida en el elemento\(2\text{,}\) que se supone que es parte del dominio.
El conjunto\(F\) sí define una función, simplemente no una con dominio\(\mathscr{N}\text{.}\) Si consideramos el conjunto más pequeño\(\mathscr{N}' = \{1,3\}\text{,}\) entonces hay una función\(f: \mathscr{N}' \rightarrow \mathscr{A}\) con\(F = \Delta (f)\text{.}\)
De nuevo escribir\(\mathscr{N} = \{1,2,3\}\)\(\mathscr{A} = \{a,b,c,d\}\text{,}\) y considerar
\ begin {ecuación*} F =\ {(1, a), (3, a), (3, d)\}\ subseteq\ mathscr {N}\ veces\ mathscr {A}\ texto {.} \ end {ecuation*}
¿Este subconjunto define una función con dominio\(\mathscr{N}\) y codominio Es\(\mathscr{A}\text{?}\) decir, existe una función\(f: \mathscr{N} \rightarrow \mathscr{A}\) tal que\(F = \Delta (f)\text{?}\) La respuesta es no, porque hay más de un par de entrada-salida con elemento de dominio\(3\text{.}\) En otro palabras, una función\(f\) con gráfico no\(\Delta (f) = F\) está bien definida, porque no tenemos forma de decir si\(f(3)\) debe ser\(a\) o\(d\text{.}\)
Recordemos que
\ begin {ecuación*}\ mathbb {Q} =\ {\ dfrac {m} {n}\ vert m, n\ in\ mathbb {Z},\, n\ ne 0\}\ text {.} \ end {equation*}
Supongamos que intentamos definir\(f: \mathbb{Q} \rightarrow \mathbb{Z}\) por\(f(\dfrac{m}{n}) = m+n\text{.}\) Esto parece una forma válida de definir una función, hasta que nos damos cuenta de que, por ejemplo,
\ begin {align*} f\ left (\ dfrac {1} {2}\ right) & = 1 + 2 = 3, & f\ left (\ dfrac {2} {4}\ right) & = 2 + 4 = 6. \ end {align*}
Esto es una tontería, porque\(\dfrac{1}{2}\) y\(\dfrac{2}{4}\) representan el mismo elemento de\(\mathbb{Q}\text{.}\) Así, regla no\(f\) está bien definida como una función, ya\(\mathbb{Q}\) que a cada elemento del dominio asocia más de un elemento del codominio\(\mathbb{Z}\text{.}\)
10.1.5: Igualdad de funciones
para\(f: A \rightarrow B\) y\(g: A\rightarrow B \text{,}\) escribir\(f = g\) si\(f(a) = g(a)\) para todos\(a\in A\)
Las funciones\(f: \mathbb{R}\rightarrow \mathbb{R}\text{,}\)\(f(x) = \vert x \vert\text{,}\) y\(g: \mathbb{R}\rightarrow \mathbb{R}\text{,}\)\(g(x) = \sqrt{x^2}\text{,}\) son iguales.
10.1.6: Imagen de una función
el conjunto de todas las salidas posibles de la función
la imagen de la función\(f: A \rightarrow B\text{,}\) para que
\ comenzar {ecuación*} f (A) =\ {f (a)\ vert a\ en A\}\ subseteq B\ final {ecuación*}
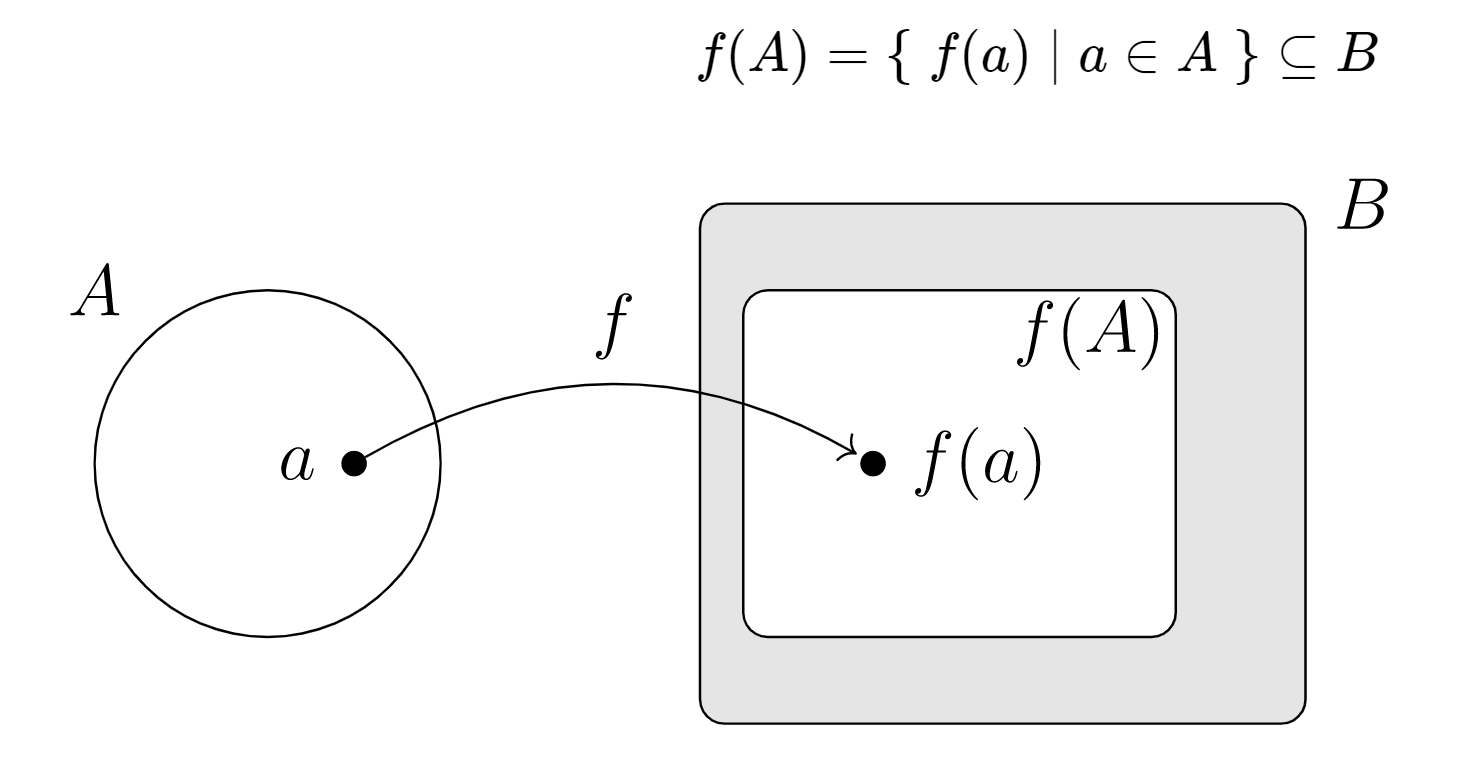
Hemos declarado antes que un codominio en una definición de función puede ser “mayor” de lo necesario porque no siempre sabemos con precisión qué elementos de salida producirá una regla de entrada y salida dada. Nuestra idea de codominio es que al menos debería decirnos qué “tipo” de salidas se producirán, pero no necesariamente exactamente qué salidas se producirán.
Con nuestro nuevo concepto de imagen de función, ahora podemos repetir esto de manera más técnica: una imagen de función es siempre un subconjunto del codominio, pero podría ser un subconjunto apropiado.
¿Cómo sabemos si un elemento de codominio es un elemento de imagen?
Para la función\(f: A \rightarrow B\) y el elemento codominio\(b\in B\text{,}\) tenemos\(b \in f(A)\) si y solo si existe\(a\in A\) tal que\(b = f(a)\text{.}\)
Considera\(f: \mathbb{R} \rightarrow \mathbb{R}\text{,}\)\(f(x) = x^2\text{.}\) Probar\(f(\mathbb{R}) = \mathbb{R}_{\geq 0}\text{,}\) dónde\(\mathbb{R}_{\geq 0}\) está el conjunto de números reales no negativos.
Solución
Después de la Prueba para la Igualdad Fija, necesitamos mostrar ambos
\ begin {align*} f (\ mathbb {R}) &\ subseteq\ mathbb {R} _ {\ geq 0}, & f (\ mathbb {R}) &\ supseteq\ mathbb {R} _ _ {\ geq 0}\ text {.} \ end {align*}
Para ser más explícitos sobre el segundo conjunto\(\mathbb{R}_{\geq 0}\text{,}\) podemos escribir
\ begin {ecuación*}\ mathbb {R} _ {\ geq 0} =\ {x\ in\ mathbb {R}\ vert x\ ge 0\}\ text {.} \ end {ecuación*}
Espectáculo\(f(\mathbb{R}) \subseteq \mathbb{R}_{\geq 0}\).
Dejar\(y\) representar un elemento arbitrario de\(f(\mathbb{R})\text{.}\) Como un elemento de la imagen de\(f\text{,}\)\(y\) es una salida correspondiente a alguna entrada. Es decir, existe alguna\(x \in \mathbb{R}\) tal que
Por lo tanto, dado que los números cuadrados son siempre positivos, tenemos\(y \ge 0\text{,}\) y por lo tanto\(y \in \mathbb{R}_{\geq 0}\text{.}\)
Espectáculo\(f(\mathbb{R}) \supseteq \mathbb{R}_{\geq 0}\).
Dejar\(y\) representar un elemento arbitrario de\(\mathbb{R}_{\geq 0}\text{.}\) Para mostrar\(y \in f(\mathbb{R})\text{,}\) necesitamos encontrar\(x \in \mathbb{R}\) tal que\(f(x) = y\text{.}\) Let\(x = \sqrt{y}\text{,}\) que se define ya que\(y \in \mathbb{R}_{\geq 0}\) implica\(y\ge 0\text{.}\) Entonces
según se desee.
el conjunto de todas las salidas de una función cuando solo se alimentan entradas de un subconjunto dado
la imagen del subconjunto\(A' \subseteq A\) bajo una función\(f: A \rightarrow B\text{,}\) para que
\ begin {ecuación*} f (A') =\ {f (a)\ vert a\ in A'\}\ subseteq B\ end {ecuación*}
Vimos en Ejemplo Trabajado\(\PageIndex{16}\) que para\(f: \mathbb{R}\rightarrow \mathbb{R} \text{,}\)\(f(x) = x^2\text{,}\) tenemos\(f(\mathbb{R}) = \mathbb{R}_{\geq 0}\text{.}\) Ahora, el conjunto de enteros\(\mathbb{Z}\) es un subconjunto del dominio\(\mathbb{R}\text{,}\) para que podamos computar
\ begin {ecuación*} f (\ mathbb {Z}) =\ {0,1,4,9,16,\ ldots, n^2,\ ldots\}\ subseteq\ mathbb {R} _ {\ geq 0}\ text {.} \ end {ecuación*}


