17.4: Graficar relaciones
- Page ID
- 118146
Recordemos que si\(R\) es una relación en un conjunto\(A\text{,}\) entonces formalmente\(R\) es un subconjunto\(A \times A\text{.}\) En otras palabras,\(R\) es una colección de pares ordenados de elementos de\(A\text{.}\)
También recordemos que en una gráfica dirigida, la colección de bordes se define formalmente como una colección de pares ordenados de vértices. Entonces, cuando el conjunto\(A\) es finito, ¡podemos considerar\(A\) como un conjunto de vértices y\(R\) como una colección de bordes (dirigidos) en una gráfica!
Para resumir, podemos representar una relación\(R \subseteq A \times A\) por la gráfica dirigida\((A,R)\text{.}\) Los vértices de la gráfica son los elementos de\(A\text{,}\) y para los elementos\(a_1,a_2 \in A\text{,}\) dibujamos una flecha desde\(a_1\) hasta\(a_2\) si\(a_1 \mathrel{R} a_2\) es verdadero.
Recordemos que para los números naturales\(m\) y\(n\text{,}\)\(m \mid n\) significa “\(m\)divide\(n\)”. Considera esta relación en el conjunto finito\(A = \{ 2,3,4,5,6,7,8,9,10 \}\text{.}\) La gráfica de esta relación aparece en la Figura\(\PageIndex{1}\).
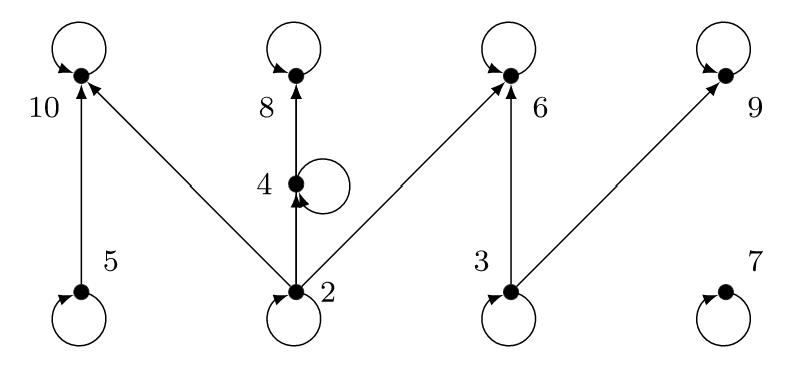
Tenga en cuenta que cada vértice tiene un bucle ya que cada número se divide a sí mismo.
Usando la misma relación de división en el\(A\) mismo conjunto que en Ejemplo\(\PageIndex{1}\) anterior, podemos obtener la gráfica para la relación inversa simplemente invirtiendo la dirección de todas las flechas en la gráfica de la Figura\(\PageIndex{1}\).
¿Cómo se reflejan en su gráfica las propiedades de una relación?
Relaciones reflexivas.
En este caso,\(a \mathrel{R} a\) es cierto para cada elemento\(a \in A\text{,}\) por lo que cada vértice tiene un bucle. Por ejemplo, la relación en Ejemplo\(\PageIndex{1}\) es reflexiva, y vemos esto reflejado en la gráfica de la Figura\(\PageIndex{1}\) por la colocación de un bucle en cada nodo.
Cuando se entiende que una relación es reflexiva, a menudo omitimos los bucles de su gráfica para reducir el desorden visual.
Relaciones simétricas.
En este caso, el condicional siempre\(a_1 \mathrel{R} a_2 \Rightarrow a_2 \mathrel{R} a_1\) es cierto. Por lo tanto, en la gráfica para\(R\text{,}\) siempre que tengamos una flecha de\(a_1\) a también\(a_2\text{,}\) debemos tener una flecha de\(a_2\) a\(a_1\text{.}\)
En el set\(A = \{a,b,c,d\}\text{,}\) la relación
\ begin {ecuación*} R =\ {(a, b), (b, a), (b, c), (c, b)\}\ end {ecuación*}
es simétrica, y vemos esta propiedad reflejada en la gráfica de la Figura\(\PageIndex{2}\), ya que cada par de nodos relacionados (distintos) tiene una flecha en cada dirección entre ellos.
 Figura\(\PageIndex{2}\): La gráfica de una relación simétrica básica.
Figura\(\PageIndex{2}\): La gráfica de una relación simétrica básica. Cuando\(R\) es simétrico, las flechas carecen esencialmente de sentido ya que entre cada par de vértices no tendremos flechas o una flecha en cada dirección. Así que también podemos dibujar la gráfica\(R\) como una gráfica ordinaria (no dirigida) en lugar de una gráfica dirigida, reemplazando cada par de flechas con un solo borde.
La relación en el ejemplo anterior se representa de manera más concisa gráficamente como en la Figura\(\PageIndex{3}\) siguiente.

Relaciones antisimétricas.
En este caso, nunca tenemos ambos\(a_1 \mathrel{R} a_2\) y\(a_2 \mathrel{R} a_1\) para\(a_1 \ne a_2\text{,}\) eso en la gráfica para\(R\text{,}\) ningún par de vértices puede tener dos flechas opuestas entre ellos.
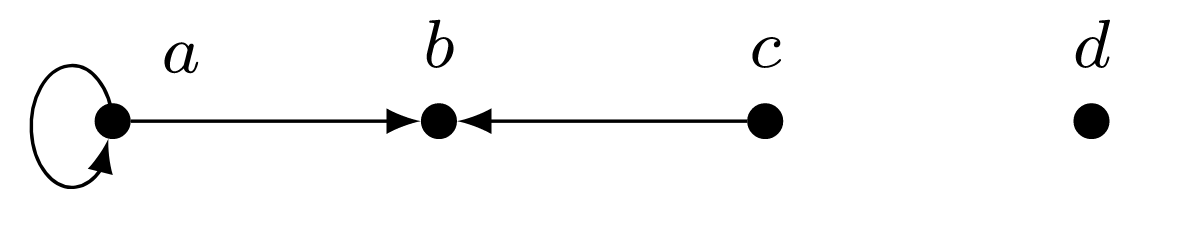
En el set\(A = \{a,b,c,d\}\text{,}\) la relación
\ begin {ecuation*} R =\ {(a, a), (a, b), (c, b)\}\ end {equation*}
es antisimétrico, y vemos esta propiedad reflejada en la gráfica de la Figura\(\PageIndex{4}\), ya que cada par de nodos distintos tiene como máximo una flecha entre ellos.
Relaciones transitivas.
En este caso, el condicional siempre\(a_1 \mathrel{R} a_2 \land a_2 \mathrel{R} a_3 \Rightarrow a_1 \mathrel{R} a_3\) es cierto. Por lo tanto, en la gráfica por\(R\text{,}\) cada “cadena” de dos flechas tiene una flecha “compuesta” correspondiente.
En el set\(A = \{a,b,c,d,e\} \text{,}\) la relación
\ begin {ecuación*} R =\ {(a, b), (b, c), (a, c), (d, e), (e, d), (d, d), (e, e)\}\ end {ecuación*}
es transitiva, y vemos esta propiedad reflejada en la gráfica de la Figura\(\PageIndex{5}\), ya que cada par de flechas que forman una “cadena” entre tres nodos tiene un correspondiente “compuesta” flecha desde el primer nodo en el cadena a la tercera.

En la gráfica de una relación transitiva, a menudo omitimos las flechas “compuestas” para reducir el desorden visual, ya que podemos inferir de “cadenas” de flechas hacia dónde irían las flechas “compuestas”. Por ejemplo, hicimos esto tanto en la gráfica de conjunto de potencia en el Ejemplo 14.4.1 (ver Figura 14.4.1) como en la gráfica de división en el Ejemplo 14.4.2 (ver Figura 14.4.2). Debería ser obvio que las relaciones “es un subconjunto de” y “divide” son transitivas, por lo que no hubo necesidad de abarrotar las gráficas de esas relaciones con flechas extra “compuestas” —podríamos rastrear el hecho de que un conjunto era un subconjunto de otro o el hecho de que un número divide a otro siguiendo una cadena de flechas a través de nodos intermedios, según sea necesario.


