20.5: Principio de encasillamiento
- Page ID
- 118121
Si\(A,B\) son conjuntos finitos con\(\vert B \vert \lt \vert A \vert\text{,}\) entonces ninguna función\(A \to B\) puede ser una inyección.
- Comprobante.
-
Este principio es justamente el contrapositivo de la Declaración 2 de Hecho 12.2.3.
Si\(m\) los objetos se colocan en\(n\) contenedores, donde\(m \gt n\text{,}\) entonces al menos un contenedor debe contener más de un objeto.
- Comprobante.
-
Dejar\(A\) ser el conjunto de objetos y\(B\) el conjunto de contenedores, de manera que
\ begin {ecuación*}\ vert B\ vert = n\ lt m =\ vert A\ vert\ vert\ texto {.} \ end {ecuation*}
También vamos a\(f: A \rightarrow B\) representar la función donde\(f(a) = b\) significa que el objeto\(a\) ha sido colocado en contenedor\(b\text{.}\) Entonces el Teorema nos\(\PageIndex{1}\) dice que\(f\) no puede ser una inyección, lo que significa que hay al menos un par de objetos distintos \(a_1,a_2\)con\(f(a_1) = f(a_2)\text{.}\)
Tu auto tiene cinco asientos, pero también tienes cinco amigos que necesitan que te lleven a casa. ¿Cómo encajarán todos?
Solución
Usando a las personas que necesitan llegar a casa (es decir, a tus amigos y a ti) como objetos y asientos de auto como contenedores, Pigeonhole Principle dice que alguien tendrá que sentarse en el regazo de otra persona.
En la cafetería se sacan pudines de\(200\) chocolate y pudines de\(200\) tapioca. Si cada\(201\) alumno toma un plato de pudín, ¿cuál es el número mínimo de pudines de tapioca que se han tomado?
Solución
Ya que no\(201 \gt 200\text{,}\) hay inyección
\ begin {ecuación*}\ {\ texto {estudiantes que tomaron un pudín}\}\ hookrightarrow\ {\ text {cuencos de pudín de chocolate}\}\ texto {.} \ end {equation*}
(O: usa a los estudiantes como objetos, cuencos de pudín de chocolate como recipientes.)
Pero en realidad no podemos hacer que dos alumnos tomen el mismo tazón de pudín, así que al menos un estudiante debe comer tapioca.
Supongamos\(A \subseteq \{1,2,\cdots, 20\}\text{.}\) Que tan grande debe\(\vert A \vert\) ser para asegurar que existan dos elementos de\(A\) cuya suma es\(21\text{?}\)
Solución
Reúne los pares (desordenados) de números que se suman a\(21\text{:}\)
\ begin {ecuación*} B =\ bigl\ {\ {1,20\},\ {2,19\},\ cdots,\ {10,11\}\ bigr\}\ subseteq\ mathscr {P} (\ {1,2,\ cdots, 20\})\ text {.} \ end {equation*}
Observe que\(\vert B \vert = 10\text{.}\) Pensando en los elementos de\(B\) como contenedores y elementos de\(A\) como objetos, colocar objeto\(a\) en contenedor\(b\) si\(a \in b\text{.}\) necesitamos un objeto más que contenedor para asegurar que algún contenedor reciba dos objetos, por lo que el la respuesta es\(\vert A \vert \ge 11\text{.}\)
Supongamos\(m \in \mathbb{N}\) y\(A \subseteq \mathbb{N}\) tal que\(0 \lt m \lt \vert A \vert \lt \infty\text{.}\) Mostrar que existen distintos\(a_1,a_2 \in A\) que tienen el mismo resto cuando se dividen por\(m\text{.}\)
Solución
El conjunto de posibles restos es\(\mathbb{N}_{<m} = \{0,1,2,\cdots,m-1\}\text{.}\) Computar el resto después de la división por\(m\) define una función\(A \to \mathbb{N}_{<m}\text{.}\) Ya que\(\vert \mathbb{N}_{<m} \vert = m \lt \vert A \vert\text{,}\) esta función no puede ser una inyección.
(O: usar elementos de\(A\) como objetos, posibles restos al dividir un número por\(m\) como contenedores).
Versión fuerte
Recordemos que dada una función\(f: A \rightarrow B\text{,}\) podemos definir una relación\(\mathord{\equiv}\) de equivalencia\(A\) tomando\(a_1 \equiv a_2\) como media\(f(a_1) = f(a_2)\) (ver Ejemplo 18.4.4). De esta manera, podemos considerar\(f\) como colocar objetos (elementos de\(A\)) en contenedores (elementos de\(B\)), de modo que ese objeto\(a \in A\) se “coloca” en contenedor\(b \in B\) cuando\(f(a) = b\text{.}\)
Supongamos\(f: A \rightarrow B\text{,}\) con\(A,B\) finito, y deja\(\mathord{\equiv}\) ser la relación de equivalencia sobre\(A\) donde\(a_1 \equiv a_2\) significa\(f(a_1) = f(a_2)\text{.}\)
Si\(\vert A \vert \gt \ell \cdot \vert B \vert\) para algunos\(\ell \in \mathbb{N}\text{,}\) entonces al menos una de las clases de equivalencia de\(A\) con respecto a\(\mathord{\equiv}\) tiene más de\(\ell\) elementos.
- Comprobante.
-
Considera lo contrapositivo:
si cada clase de equivalencia de no\(A\) tiene más que\(\ell\) elementos, entonces\(\vert A \vert \le \ell \cdot \vert B \vert\text{.}\)
Ya que\(B\) es finito y\(f(A) \subseteq B\text{,}\) luego también\(f(A)\) es finito y podemos enumerar sus elementos. Escribir\(f(A) = \{ b_1, b_2, \cdots, b_n \}\text{.}\) Cada elemento de\(f(A)\) corresponde a una clase de equivalencia de\(A\text{.}\)
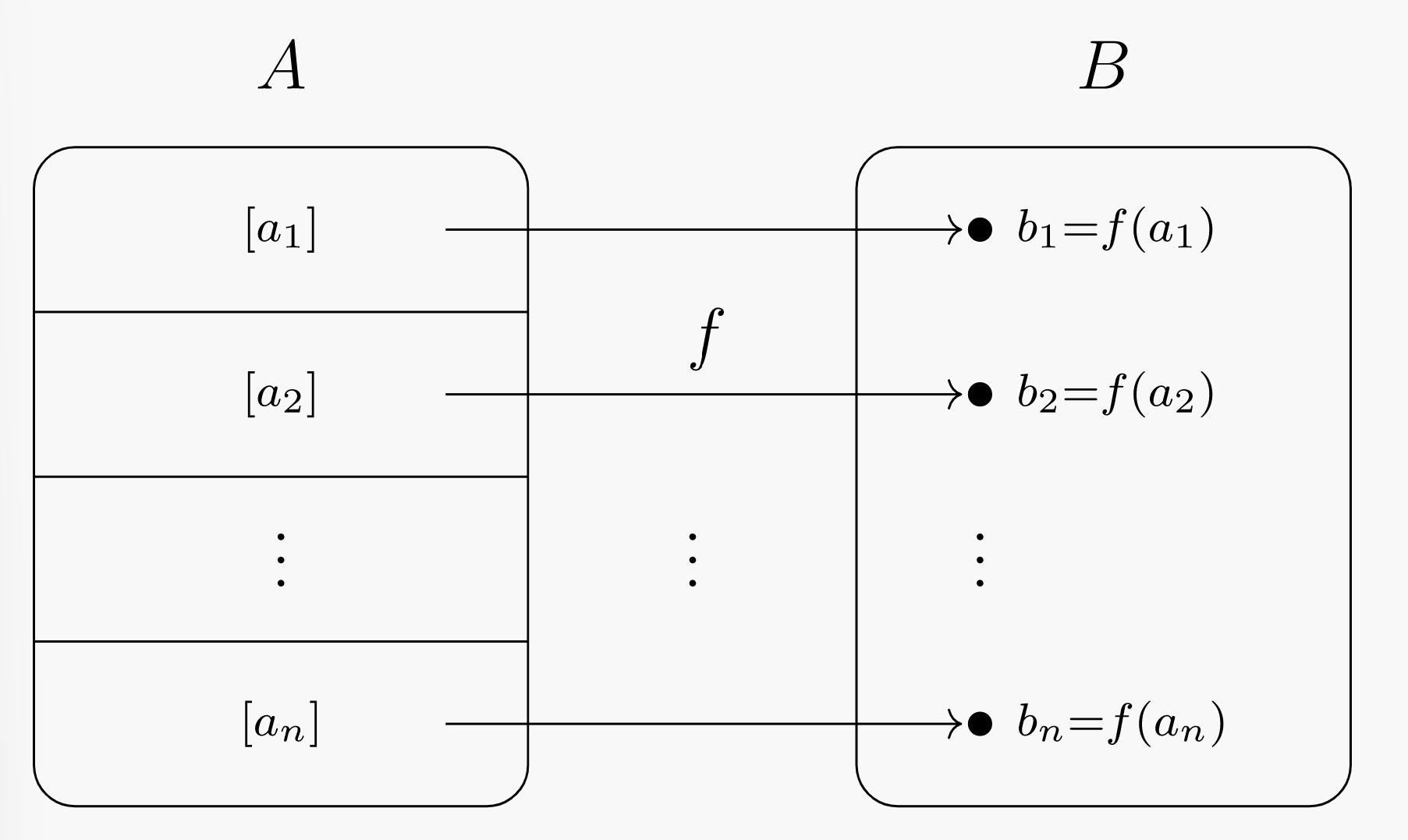
Figura\(\PageIndex{1}\): Diagrama de clases de equivalencia bajo la equivalencia “tener la misma imagen”. En este diagrama, los\(a_i\) son elementos representativos de la clase de elementos de los\(A\) que se mapean\(b_i\) por\(f\text{.}\) En particular, debemos tener\(f(a_i) = b_i\) para cada índice\(i\text{.}\)
Estamos asumiendo que cada clase no\([a_i]\) contiene más que\(\ell\) elementos; es decir,\(\vert [a_i] \vert \le \ell\text{.}\) Dado que una relación de equivalencia siempre divide un conjunto\(A\) en la unión disjunta de sus clases de equivalencia, tenemos
\ begin {align*}\ vert A\ vert & =\ vert [a_1]\ vert +\ vert [a_2]\ vert +\ cdots +\ vert [a_n]\ vert\\ vert\ &\ le\ underbrackets {\ ell +\ ell +\ cdots +\ ell} _ {r\ text {terms}}\\ & =\ ell n\ & =\ ell\ cdot\ vert f (A)\ vert. \ end {align*}
Pero\(f(A)\) es un subconjunto del conjunto finito\(B\text{,}\) y así\(\vert f(A) \vert \le \vert B \vert\text{.}\) Combinando esto con el cálculo anterior da\ begin {ecuación*}\ vert A\ vert\ le\ ell\ cdot\ vert f (A)\ vert\ le\ ell\ cdot\ vert B\ vert\ text {.} \ end {ecuación*}
Si\(m\) los objetos se colocan en\(n\) contenedores, con\(m \gt \ell n \) para algunos\(\ell \in \mathbb{N}\text{,}\) entonces al menos un contenedor contiene más de\(\ell\) objetos.
- Idea de Prueba.
-
Nuevamente, dejemos\(A\) ser el conjunto de objetos y\(B\) el conjunto de contenedores, para que
\ begin {ecuación*}\ vert A\ vert = m\ gt\ ell n =\ ell\ cdot\ vert B\ vert\ text {.} \ end {equation*}
Luego aplica el Principio de Pigeonhole (forma fuerte, versión formal).
El Principio Pigeonhole (forma fuerte, versión formal) es una generalización del Principio Pigeonhole (versión formal). Una función es una inyección precisamente cuando no hay dos elementos distintos del dominio que producen la misma imagen de salida, por lo que usar\(\ell = 1\) en la forma fuerte devuelve la forma original.
Demostrar que si se distribuyen trece monedas a seis niños, entonces al menos un niño recibirá al menos tres monedas.
Solución
Usando monedas como objetos y niños como contenedores, la declaración dada es solo el Principio de Pigeonhole (forma fuerte, versión formal) con que\(\ell = 2\text{:}\) tenemos\(13\) objetos y\(6\) contenedores, y\(13 \gt 2 \cdot 6\text{.}\) (Nota: Dado que las monedas son objetos discretos, “más de dos” y “al menos tres” son lo mismo.)
Vale la pena pensar en cómo se podría probar directamente la forma fuerte del Principio de Pigeonhole. Considere el diagrama en la Figura\(\PageIndex{1}\): el “punto de inflexión” entre\(\vert A \vert \le \ell \cdot \vert B \vert\) y\(\vert A \vert \gt \ell \cdot \vert B \vert\) es cuando\(f\) es suryectiva y cada una de las clases de equivalencia tiene exactamente\(\ell\) elementos. Cuando\(f\) es suryectiva, hay clases de\(\vert B \vert\) equivalencia en\(A\text{.}\) Ya que\(A\) es la unión disjunta de sus clases de equivalencia bajo\(\equiv\text{,}\) tenemos\(\vert A \vert = \ell \cdot \vert B \vert\text{.}\) Si le agregamos un elemento más habrá\(A\text{,}\) que incluirse en una de las equivalencias clases, y esa clase ahora tendrá un tamaño mayor que\(\ell\text{.}\)
La cafetería pone pudines de\(100\) chocolate,\(100\) tapioca y\(100\) caramelo. ¿Cuántos estudiantes deben tomar un pudín antes de que podamos estar seguros de que al menos uno de los sabores tiene al menos la mitad de los cuencos tomados?
Solución. 1 Usando el pensamiento de “punto de inflexión”
El “punto de inflexión” es exactamente\(49\) cuencos de cada sabor tomado, lo que requiere que\(3\cdot 49 = 147\) los estudiantes. Después del\(148^{th}\) alumno, definitivamente tendremos\(50\) cuencos de uno de los sabores tomados.
Solución. 2 Uso directo del Principio de Agujero
Considera a los estudiantes como objetos (\(m\)de ellos — esto es lo desconocido por determinar) y los sabores como recipientes (\(3\)de ellos). Para determinar el valor apropiado de\(\ell\) usar, considere que “al menos la mitad” en este problema significa “al menos\(50\)”, que es lo mismo que “más de\(49\)”. Así que elige\(\ell = 49\text{.}\) En ese caso, necesitamos\(m \gt 49 \cdot 3 = 147\text{,}\) llevarnos a la respuesta de\(m = 147 + 1 = 148\) los alumnos.


