6.3: Funciones uno a uno

Última actualización
Guardar como PDF

Page ID: 112971

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Distinguimos dos familias especiales de funciones: las funciones uno-a-uno y las funciones onto. Discutiremos las funciones uno a uno en esta sección, y sobre las funciones en la siguiente.

Definición: Inyección

Se dice que una función${f}:{A}\to{B}$ es uno a uno si

\[x_1\neq x_2 \Rightarrow f(x_1)\neq f(x_2) \nonumber\]

para todos los elementos$x_1,x_2\in A$. Una función uno a uno también se llama inyección, y llamamos a una función inyectable si es uno a uno. Una función que no es uno a uno se conoce como muchos a uno.

Cualquier función bien definida es uno a uno o muchos a uno. Una función no puede ser uno a muchos porque ningún elemento puede tener múltiples imágenes. La diferencia entre funciones uno a uno y muchos a uno es si existen elementos distintos que comparten la misma imagen. No hay imágenes repetidas en una función uno a uno.

Ejemplo$\PageIndex{1}\label{eg:oneonefcn-01}$

La función de identidad en cualquier conjunto no vacío$A$\[{i_A}:{A}\to{A}, \qquad i_A(x)=x, \nonumber\] asigna cualquier elemento a sí mismo. Es claro que todas las funciones de identidad son uno-a-uno.

Ejemplo$\PageIndex{2}\label{eg:oneonefcn-02}$

La función$ h : {A}\to{A}$ definida por$h(x)=c$ para algún elemento fijo$c\in A$, es un ejemplo de una función constante. Es una función con una sola imagen. Esto es exactamente lo contrario de una función de identidad. Claramente no es uno a uno a menos que$|A|=1$.

Para dominios con un pequeño número de elementos, se puede utilizar la inspección en las imágenes para determinar si la función es uno a uno. Esto se vuelve imposible si el dominio contiene un mayor número de elementos.

En la práctica, es más fácil usar el contrapositivo de la definición para probar si una función es uno a uno:

\[f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \nonumber\]

Ejemplo$\PageIndex{3}\label{eg:oneonefcn-03}$

¿La función está$ f : {\mathbb{R}}\to{\mathbb{R}}$ definida por$f(x)=3x+2$ uno a uno?

Solución: Asumir$f(x_1)=f(x_2)$, lo que significa\[3x_1+2 = 3x_2+2. \nonumber\] Así$3x_1=3x_2$, lo que implica eso$x_1=x_2$. Por lo tanto$f$ es uno a uno.

ejercicio$\PageIndex{1}\label{he:oneonefcn-01}$

Determinar si la función$ g : {\mathbb{R}}\to{\mathbb{R}}$ definida por$g(x)=5-7x$ es uno a uno.

ejercicio$\PageIndex{2}\label{he:oneonefcn-02}$

Determinar si la función$ h : {[2,\infty)}\to{\mathbb{R}}$ definida por$h(x)=\sqrt{x-2}$ es uno a uno.

Curiosamente, a veces podemos usar el cálculo para determinar si una función real es uno a uno. Una función real$f$ está aumentando si\[x_1 < x_2 \Rightarrow f(x_1) < f(x_2), \nonumber\] y disminuyendo si\[x_1 < x_2 \Rightarrow f(x_1) > f(x_2). \nonumber\] Obviamente, tanto las funciones crecientes como decrecientes son uno-a-uno. A partir del cálculo, sabemos que

Una función está aumentando a lo largo de un intervalo abierto$(a,b)$ si es$f'(x)>0$ para todos$x\in(a,b)$.
Una función está disminuyendo durante un intervalo abierto$(a,b)$ si es$f'(x)<0$ para todos$x\in(a,b)$.

Por lo tanto, si la derivada de una función es siempre positiva, o siempre negativa, entonces la función debe ser uno a uno.

Ejemplo$\PageIndex{4}\label{eg:oneonefcn-04}$

La función$p : {\mathbb{R}}\to{\mathbb{R}}$ definida por\[p(x) = 2x^3-5 \nonumber\] es uno a uno, porque$p'(x)=6x^2>0$ para cualquier$x\in\mathbb{R}^*$. Asimismo, la función$q:{\big(-\frac{\pi}{2},\frac{\pi}{2}\big)}\to{\mathbb{R}}$ definida por\[q(x) = \tan x \nonumber\] es también uno a uno, porque$q'(x) = \sec^2x > 0$ para cualquiera$x\in \big(-\frac{\pi}{2},\frac{\pi}{2}\big)$.

ejercicio$\PageIndex{3}\label{he:oneonefcn-03}$

Usa ambos métodos para mostrar que la función$k:{(0,\infty)}\to{\mathbb{R}}$ definida por$k(x) = \ln x$ es uno-a-uno.

Ejemplo$\PageIndex{5}\label{eg:oneonefcn-05}$

La función$ h : {\mathbb{R}}\to{\mathbb{R}}$ dada por no$h(x)=x^2$ es uno-a-uno porque algunas de sus imágenes son idénticas. Por ejemplo,$h(3) = h(-3) =9$. Es una función de muchos a uno. Asimismo, la función de valor absoluto no$|x|$ es uno a uno.

Las funciones$p:{[\,0,\infty)}\to{\mathbb{R}}$ definidas por$p(x)=x^2$ y$q:{[\,0,\infty)}\to{\mathbb{R}}$ definidas por$q(x)=|x|$ son uno-a-uno. Que una función sea uno a uno depende no sólo de su fórmula, sino también de su dominio. En consecuencia, a veces podemos convertir una función de muchos a uno en una función uno a uno modificando su dominio.

Ejemplo$\PageIndex{6}\label{eg:onetoone}$

Construir una función uno a uno de$[\,1,3\,]$ a$[\,2,5\,]$.

Solución

Hay muchas soluciones posibles. En cualquier caso, comience con una gráfica. Podemos usar una gráfica de línea recta. El dominio$[\,1,3\,]$ se encuentra en el$x$ eje -y el codominio$[\,2,5\,]$ se encuentra en el$y$ eje -eje. De ahí que la gráfica debe cubrir la región encajonada en la Figura$\PageIndex{1}$.

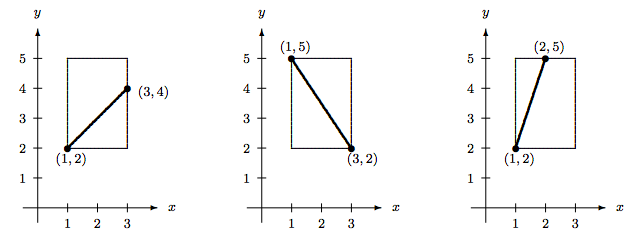
Screen Shot 2020-01-13 at 10.53.29 AM.png — Figura$\PageIndex{1}$: Tres candidatos para funciones uno a uno de [1,3] a [2,5].

Las tres gráficas no producen imágenes duplicadas. Necesitamos cubrir todos los$x$ valores de 1 a 3 para que la función esté bien definida. Esto deja solo las dos primeras gráficas como ejemplos legítimos.

Para determinar la fórmula para$f$, necesitamos derivar la ecuación de la línea. Toma la primera gráfica como nuestra elección. La línea une el punto$(1,2)$ al punto$(3,4)$. Así, su ecuación es\[\frac{y-2}{x-1} = \frac{4-2}{3-1} = 1. \nonumber\] El último paso es escribir la respuesta en forma de$f(x)=\ldots\,$. Tenemos que expresarnos$y$ en términos de$x$. Nos encontramos$y = x+1$. De ahí,\[ f : {[\,1,3\,]}\to{[\,2,5\,]}, \qquad f(x) = x+1 \nonumber\] es un ejemplo de una función uno-a-uno.

ejercicio$\PageIndex{4}\label{he:oneonefcn-04}$

Construya una función uno a uno de$[\,1,3\,]$ a$[\,2,5\,]$ basándose en la segunda gráfica del Ejemplo 6.3.6.

ejercicio$\PageIndex{5}\label{he:oneonefcn-05}$

Construir una función uno a uno de$[\,3,8\,]$ a$[\,2,5\,]$.

ejemplo$\PageIndex{7}\label{eg:gmod43}$

Determinar si la función$ g : {\mathbb{Z}_{43}}\to{\mathbb{Z}_{43}}$ definida por\[g(x) \equiv 11x-5 \pmod{43} \nonumber\] es uno a uno.

Solución: Asumir$g(x_1)=g(x_2)$. Esto significa\[11x_1 - 5 \equiv 11x_2 - 5 \pmod{43}, \nonumber\] lo que implica\[11x_1 \equiv 11x_2 \pmod{43}. \nonumber\] Notar que$4\cdot11=44\equiv1$ (mod 43), de ahí$11^{-1}\equiv4$ (mod 43). Multiplicando 4 a ambos lados de la última congruencia rinde\[44 x_1 \equiv 44 x_2 \pmod{43}, \nonumber\] lo que equivale a, ya que$44\equiv1$ (mod 43),\[x_1 \equiv x_2 \pmod{43}. \nonumber\] Por lo tanto,$x_1=x_2$ en$\mathbb{Z}_{43}$. Esto demuestra que$g$ es uno a uno.

ejercicio$\PageIndex{6}\label{he:oneonefcn-06}$

¿La función está$ h : {\mathbb{Z}_{15}}\to{\mathbb{Z}_{15}}$ definida por\[h(x) \equiv 4x-11 \pmod{15} \nonumber\] una función uno a uno?

ejercicio$\PageIndex{7}\label{he:oneonefcn-07}$

Demostrar que la función$k:{\mathbb{Z}_{15}}\to{\mathbb{Z}_{15}}$ definida por no\[k(x) \equiv 5x-11 \pmod{15} \nonumber\] es uno-a-uno al encontrar$x_1\neq x_2$ tal que$k(x_1)=k(x_2)$.

Ejemplo$\PageIndex{8}\label{eg:oneonefcn-08}$

En el último ejercicio, no debemos confiar en la inexistencia de$5^{-1}$ in$\mathbb{Z}_{15}$ para demostrar que no$k$ es uno a uno. Se debe considerar la interacción entre el dominio, el codominio y la definición de la función. Por ejemplo, a pesar de que$5^{-1}$ no existe en$\mathbb{Z}_{15}$, la función$p :{\mathbb{Z}_3}\to{\mathbb{Z}_{15}}$ definida por\[p(x) \equiv 5x-11 \pmod{15} \nonumber\] es uno-a-uno, porque$p(0)=4$,$p(1)=9$, y$p(2)=14$ son imágenes distintas.

El último ejemplo ilustra la dificultad en una función con diferentes módulos en su dominio y codominio. ¡Tenga precaución cuando se ocupe de tales funciones! En ocasiones, los sets infinitos también plantean un reto. Debido a que hay un suministro infinito de elementos, podemos obtener resultados que parecen imposibles para conjuntos finitos.

Ejemplo$\PageIndex{9}\label{eg:oneonefcn-09}$

La función$ f : {\mathbb{Z}}\to{\mathbb{Z}}$ definida por no\[f(n) = \cases{ \frac{n}{2} & if $n$ is even \cr \frac{n+1}{2} & if $n$ is odd \cr} \nonumber\] es uno-a-uno, porque, por ejemplo,$f(0)=f(-1)=0$. La función$ g : {\mathbb{Z}}\to{\mathbb{Z}}$ definida por\[g(n) = 2n \nonumber\] es uno a uno, porque si$g(n_1)=g(n_2)$, entonces$2n_1=2n_2$ implica eso$n_1=n_2$.

ejercicio$\PageIndex{8}\label{he:oneonefcn-08}$

Mostrar que la función$ h : {\mathbb{Z}}\to{\mathbb{N}}$ definida por\[h(n) = \cases{ 2n+1 & if $n\geq0$, \cr -2n & if $n < 0$, \cr} \nonumber\] es uno a uno.

Ejemplo$\PageIndex{10}\label{eg:oneonefcn-10}$

$A$Sea el conjunto de todos los individuos casados de una comunidad monógama que no estén divorciados ni viudos. Entonces la función$s:{A}\to{A}$ definida por\[s(x) = \mbox{ spouse of } x \nonumber\] es uno a uno. La razón es, es imposible tener$x_1\neq x_2$ y sin embargo$s(x_1)=s(x_2)$.

Resumen y revisión

Se dice que una función$f$ es uno a uno si$f(x_1) = f(x_2) \Rightarrow x_1=x_2$.
No hay dos imágenes de una función uno a uno iguales.
Para mostrar que una función no$f$ es uno-a-uno, todo lo que necesitamos es encontrar dos$x$ valores distintos que produzcan la misma imagen; es decir, encontrar$x_1\neq x_2$ tal que$f(x_1)=f(x_2)$.

Ejercicio$\PageIndex{1}\label{ex:oneonefcn-01}$

¿Cuáles de las siguientes funciones son uno-a-uno? Explicar.

$ f : {\mathbb{R}}\to{\mathbb{R}}$,$f(x)=x^3-2x^2+1$.
$ g : {[\,2,\infty)}\to{\mathbb{R}}$,$f(x)=x^3-2x^2+1$.

Ejercicio$\PageIndex{2}\label{ex:oneonefcn-02}$

¿Cuáles de las siguientes funciones son uno-a-uno? Explicar.

$p :{\mathbb{R}}\to{\mathbb{R}}$,$h(x)=e^{1-2x}$.
$ q :{\mathbb{R}}\to{\mathbb{R}}$,$p(x)=|1-3x|$.

Ejercicio$\PageIndex{3}\label{ex:oneonefcn-03}$

Construye una función uno a uno$ f : {(1,3)}\to{(2,5)}$ para que siga$ f : {[\,1,3)}\to{[\,2,5)}$ siendo uno a uno.

Ejercicio$\PageIndex{4}\label{ex:oneonefcn-04}$

Construir una función uno a uno$ g : {[\,2,5)}\to{(1,4\,]}$.

Ejercicio$\PageIndex{5}\label{ex:oneonefcn-05}$

Determine cuáles de las siguientes son funciones uno-a-uno.

$ f : {\mathbb{Z}}\to{\mathbb{Z}}$;$f(n)=n^3+1$
$ g : {\mathbb{Q}}\to{\mathbb{Q}}$;$g(x)=n^2$
$ h : {\mathbb{R}}\to{\mathbb{R}}$;$h(x)=x^3-x$
${k} : {\mathbb{R}}\to{\mathbb{R}}$;$k(x)=5^x$

Ejercicio$\PageIndex{6}\label{ex:oneonefcn-06}$

Determine cuáles de las siguientes son funciones uno-a-uno.

$p :{\wp(\{1,2,3,\ldots,n\})}\to{\{0,1,2,\ldots,n\}}$;$p(S)=|S|$
$ q :{\wp(\{1,2,3,\ldots,n\})}\to{\wp(\{1,2,3,\ldots,n\})}$;$q(S)=\overline{S}$

Ejercicio$\PageIndex{7}\label{ex:oneonefcn-07}$

Determinar cuáles de las siguientes funciones son uno-a-uno.

${f_1}:{\{1,2,3,4,5\}}\to{\{a,b,c,d\}}$;$f_1(1)=b$,$f_1(2)=c$,$f_1(3)=a$,$f_1(4)=a$,$f_1(5)=c$
${f_2}:{\{1,2,3,4\}}\to{\{a,b,c,d,e\}}$;$f_2(1)=c$,$f_2(2)=b$,$f_2(3)=a$,$f_2(4)=d$
${f_3}:{\mathbb{Z}}\to{\mathbb{Z}}$;$f_5(n)=-n$
$f_4: \mathbb{Z} \rightarrow \mathbb{Z}$;$f_4(n) = \cases{ 2n & if $n < 0$, \cr -3n & if $n\geq0$,\cr}$

Ejercicio$\PageIndex{8}\label{ex:oneonefcn-08}$

Determinar cuáles de las siguientes funciones son uno-a-uno.

${g_1}:{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}$;$g_1(1)=b$,$g_1(2)=b$,$g_1(3)=b$,$g_1(4)=a$,$g_1(5)=d$
${g_2}:{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}$;$g_2(1)=d$,$g_2(2)=b$,$g_2(3)=e$,$g_2(4)=a$,$g_2(5)=c$
$g_3: \mathbb{N} \rightarrow \mathbb{N}$;$g_3 (n) = \cases{ \frac{n+1}{2} & if $n$ is odd \cr \frac{n}{2} & if $n$ is even \cr}$
$g_4: \mathbb{N} \rightarrow \mathbb{N}$;$g_4 (n) = \cases{ n+1 & if $n$ is odd \cr n-1 & if $n$ is even \cr}$

Ejercicio$\PageIndex{9}\label{ex:oneonefcn-09}$

Enumere todas las funciones uno a uno de$\{1,2\}$ a$\{a,b,c,d\}$.

Pista: Enumere las imágenes de cada función.

Ejercicio$\PageIndex{10}\label{ex:oneonefcn-10}$

¿Es posible encontrar una función uno a uno de$\{1,2,3,4\}$ a$\{1,2\}$? Explicar.

Ejercicio$\PageIndex{11}\label{ex:oneonefcn-11}$

Determinar cuáles de las siguientes funciones son uno-a-uno.

$ f : {\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}$;$h(n)\equiv 3n$ (mod 10).
$ g : {\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}$;$g(n)\equiv 5n$ (mod 10).
$ h : {\mathbb{Z}_{36}}\to{\mathbb{Z}_{36}}$;$h(n)\equiv 3n$ (mod 36).

Ejercicio$\PageIndex{12}\label{ex:oneonefcn-12}$

Determinar cuáles de las siguientes funciones son uno-a-uno.

$r:{\mathbb{Z}_{36}}\to{\mathbb{Z}_{36}}$;$r(n)\equiv 5n$ (mod 36).
$s:{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}$;$s(n)\equiv n+5$ (mod 10).
$t:{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}$;$t(n)\equiv 3n+5$ (mod 10).

Ejercicio$\PageIndex{13}\label{ex:oneonefcn-13}$

Determinar cuáles de las siguientes funciones son uno-a-uno.

$\alpha:{\mathbb{Z}_{12}}\to{\mathbb{Z}_{ 7}}$;$\alpha(n)\equiv 2n$ (mod 7).
$\beta :{\mathbb{Z}_{ 8}}\to{\mathbb{Z}_{12}}$;$\beta (n)\equiv 3n$ (mod 12).
$\gamma:{\mathbb{Z}_{ 6}}\to{\mathbb{Z}_{12}}$;$\gamma(n)\equiv 2n$ (mod 12).
$\delta:{\mathbb{Z}_{12}}\to{\mathbb{Z}_{36}}$;$\delta(n)\equiv 6n$ (mod 36).

Ejercicio$\PageIndex{14}\label{ex:oneonefcn-14}$

Dar un ejemplo de una función uno-a-uno$f$ desde$\mathbb{N}$$\mathbb{N}$ que no es la función de identidad.