1.1: Composiciones y Particiones

Última actualización
Guardar como PDF

Page ID: 113168

Leo Moser
University of Alberta via The Trilla Group

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Consideramos problemas relacionados con el número de formas en que un número puede escribirse como suma. Si se toma en cuenta el orden de los términos en la suma la suma se denomina composición y el número de composiciones de$n$ se denota por$c(n)$. Si no se toma en cuenta el orden la suma es una partición y el número de particiones de$n$ se denota por$p(n)$. Así, las composiciones de 3 son

3 = 3, 3 = 1 + 2, 3 = 2 + 1 y 3 = 1 + 1 + 1,

para que$c(3) = 4$. Las particiones de 3 son

3 =3, 3 = 2 + 1, y 3 = 1 + 1 + 1,

así$p(3) = 3$.

Existen esencialmente tres métodos para obtener resultados en composiciones y particiones. Primero por argumentos puramente combinatorios, segundo por argumentos algebraicos con series generadoras, y finalmente por operaciones analíticas sobre la serie generadora. Discutiremos solo los dos primeros de estos métodos.

Consideramos primeras composiciones, siendo estas más fáciles de manejar que las particiones. La función$c(n)$ se determina fácilmente de la siguiente manera. Considerar$n$ escrito como una suma de 1's, tenemos$n - 1$ espacios entre ellos y en cada uno de los espacios podemos insertar un slash, cediendo$2^{n - 1}$ posibilidades corrsponding a la$2^{n - 1}$ composición de$n$. Por ejemplo

3 = 1 1, 3 = 1/1 1, 3 = 1 1/1, 3 = 1/1/1.

Solo para ilustrar el método algebraico en este caso bastante trivial consideramos

$\sum_{\infty}^{n = 1} c(n)x^n$.

Se verifica fácilmente que

$\begin{array} {rcl} {\sum_{n = 1}^{\infty} c(n) x^n} &= & {\sum_{m = 1}^{\infty} (x + x^2 + x^3 + \cdot \cdot \cdot)^m} \\ {} &= & {\sum_{m = 1}^{\infty} (\dfrac{x}{1 - x})^m = \dfrac{x}{1 - 2x} = \sum_{n =1}^{\infty} x^{n - 1}x^n.} \end{array}$

Ejemplo$\PageIndex{1}$

Como ejercicio sugeriría usar tanto el método combinatorio como el enfoque algebraico para probar los siguientes resultados:

El número de composiciones de exactamente$n$ en$m$ partes es${n - 1 \choose m -1}$ (catalán);
El número de composiciones de$n$ en partes pares es$2^{\dfrac{n}{2} - 1}$ si$n$ es par y 0 si$n$ es impar;
El número de composiciones de$n$ en un número par de partes es igual al número de composiciones de$n$ en un número impar de partes.

Solución

Agrega texto aquí.

Algo más interesante es la determinación del número de composiciones$c^{*}(n)$ de$n$ en partes impares. Aquí el enfoque algebraico rinde

$\begin{array} {rcl} {\sum_{n = 1} c^{*}(n) x^n} &= & {\sum_{m = 1}^{\infty} (x + x^3 + x^5 + \cdot \cdot \cdot)^m} \\ {} &= & {\sum_{m = 1}^{\infty} (\dfrac{x}{1 - x^2})^m = \dfrac{x}{1 - x - x^2} = \sum F(n) x^n.} \end{array}$

Al multiplicar cruzando las dos últimas expresiones vemos que

$F_{n + 2} = F_{n} + F_{n + 1}$,$F_0 = 0, F_1 = 1$

Así las F son los llamados números de Fibonacci

1, 1, 2, 3, 5, 8, 13,...

La función generadora produce dos expresiones explícitas para estos números. Primero, por “fraccionamiento parcial”$\dfrac{x}{1 - x - x^2}$, expandiendo cada término como una serie de potencias y comparando coeficientes, obtenemos

$F_n = \dfrac{1}{\sqrt{5}}{(\dfrac{1 + \sqrt{5}}{2})^n - (\dfrac{1 - \sqrt{5}}{2})^n}.$

Otra expresión para$F_n$ se obtiene observando que

$\dfrac{x}{1 - x - x^2} = x(1 + (x + x^2)^1 + (x + x^2)^2 + (x + x^2)^3 + \cdot\cdot\cdot).$

Comparando los coeficientes aquí obtenemos (Lucas)

$F_n = {n - 1 \choose 0} + {n - 2 \choose 1} + {n - 3 \choose 2} + \cdot\cdot\cdot).$

Se podría considerar el problema de deducir esta fórmula por argumentos combinatorios.

Supongamos que denotamos por$a(n)$ el número de composiciones de n con todos los summands como máximo 2, y por b (n) el número de composiciones de$n$ con todos los summands al menos 2. Un resultado interesante es ese$a(n) = b(n + 2)$. Voy a probar este resultado y sugerir el problema de encontrar una generalización razonable.

Primero tenga en cuenta que$a(n) = a(n − 1) + a(n − 2)$. Esto se desprende del hecho de que toda composición admisible termina en 1 ó 2. Al eliminar este último summand, obtenemos una composición admisible de$n − 1$ y$n − 2$ respectivamente. Desde$a(1) = 1$ y$a(2) = 2$, se deduce que$a(n) = F_n$. La función$b(n)$ satisface la misma fórmula de recursión. De hecho, si el último sumatorio en una composición admisible de$n$ es 2, suprimirlo para obtener una composición admisible de$n − 2$; si el último sumatorio es mayor a 2, reducirlo en 1 para obtener una composición admisible de$n − 1$. Ya que$b(2) = b(3) = 1$, se deduce$b(n) = F_{n−2}$ que para que$a(n)=F_n =b(n+2)$.

Una idea interesante para las composiciones es la del peso de una composición. Supongamos que asociamos con cada composición un número llamado el peso, que es el producto de los summands. Determinaremos la suma$w(n)$ de los pesos de las composiciones de$n$. La función generadora de$w(n)$ es

$\sum_{n = 1}^{\infty} w(n) x^n = \sum_{m = 1}^{\infty} (x + 2x^2 + 3x^3 + \cdot\cdot\cdot)^m = \dfrac{x}{1 - 3x + x^2}.$

De esto nos encontramos con eso$w(n)=3w(n − 1) − w(n − 2)$. Lo dejo como ejercicio para demostrar a partir de esto que$w(n) = F_{2n−1}$.

Pasamos ahora a las particiones. No existe una fórmula explícita simple para$p(n)$. Nuestro principal objetivo aquí será probar la fórmula de recursión

$p(n) = p(n - 1) + p(n - 2) - p(n - 5) - p(n - 7) + p(n - 12) + p(n - 15) + \cdot\cdot\cdot$

descubierto por Euler. El enfoque algebraico de la teoría de particiones depende de manipulaciones algebraicas con la función generadora

$\sum_{n = 0}^{\infty} p(n)x^n = \dfrac{1}{(1 - x)(1 - x^2)(1 - x^3) \cdot\cdot\cdot}$

y funciones relacionadas para particiones restringidas. El enfoque combinatorio depende del uso de diagramas de partición (Ferrer). Por ejemplo el diagrama Ferrer de la partición 7 = 4 + 2 + 1 es

$Screen Shot 2019-10-20 a las 8.42.16 PM.png$

Aquí es útil la noción de partición conjugada. Esto se obtiene reflejando el diagrama en una$45^{\circ}$ línea que baja desde la esquina superior izquierda. Por ejemplo,

las particiones

$Screen Shot 2019-10-20 a las 8.47.04 PM.png$ y $Screen Shot 2019-10-20 a las 8.47.14 PM.png$

se conjugan entre sí. Esta correspondencia arroja casi inmediatamente los siguientes teoremas:

El número de particiones de$n$ en$m$ partes es igual al número de particiones de$n$ en partes la mayor de las cuales es$m$;
El número de particiones de$n$ en no más de$m$ partes es igual al número de particiones de $n$en partes que no excedan$m$.

De una naturaleza algo diferente es la siguiente: El número de particiones de$n$ en partes impares es igual al número de particiones de$n$ en partes distintas. Para ello damos una prueba algebraica. Usando funciones generadoras bastante obvias para las particiones requeridas, el resultado se reduce a mostrar que

$\dfrac{1}{(1 - x)(1 - x^3)(1 - x^5)(1 - x^7)\cdot\cdot\cdot} = (1 + x)(1 + x^2)(1 + x^3)(1 + x^4)\cdot\cdot\cdot.$

La multiplicación cruzada hace que el resultado sea intuitivo.
Pasamos ahora a un teorema más importante debido a Euler:

$(1 - x)(1 - x^2)(1 - x^3)\cdot\cdot\cdot = 1 - x^1 - x^2 + x^5 + x^7 - x^{12} - x^{15} + \cdot\cdot\cdot,$

donde los exponentes son los números de la forma$\dfrac{1}{2} k(3k \pm 1)$. Primero notamos que

$(1 - x)(1 - x^2)(1 - x^3) \cdot\cdot\cdot = \sum((E(n) - O(n))x^n,$

donde$E(n)$ es el número de particiones de$n$ en un número par de partes distintas y$O(n)$ el número de particiones$n$ en un número impar de partes distintas.

Tratamos de establecer una correspondencia uno a uno entre particiones de las dos clases consideradas. Tal correspondencia, naturalmente, no puede ser exacta, ya que una correspondencia exacta lo demostraría$E(n) = O(n)$.

Tomamos una gráfica que representa una partición de$n$ en cualquier número de partes desiguales. Llamamos a la línea más baja$AB$ la base de la gráfica. Desde$C$, el nodo extremo noreste, dibujamos la línea sur-oeste más larga posible en la gráfica; esta puede contener solo un nodo. Esta línea$CDE$ se llama el ala de la gráfica

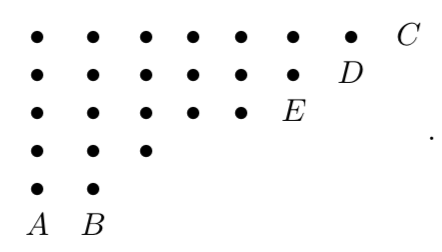
$Screen Shot 2019-10-20 a las 8.56.40 PM.png$

Por lo general, podemos mover la base a la posición de una nueva ala (paralela y a la derecha del ala “vieja”). En ocasiones podemos llevar a cabo la operación inversa (moviendo el ala para estar sobre la base, por debajo de la base antigua). Cuando la operación descrita o su inversa es posible, conduce de una partición con a un número impar de partes a un número par de partes o a la inversa. Así, en general$E(n) = O(n)$. Sin embargo, dos casos requieren una atención especial,. Están tipificados por los diagramas

$Screen Shot 2019-10-20 a las 8.57.17 PM.png$ y $Screen Shot 2019-10-20 a las 8.57.41 PM.png$

En estos casos$n$ tiene la forma

$k + (k + 1) + \cdot\cdot\cdot + (2k - 1) = \dfrac{1}{2} (3k^2 - k)$

$(k + 1) + (k + 2) + \cdot\cdot\cdot + (2k) = (3k^2 + k)$.

En ambos casos hay un exceso de una partición en un número par de partes, o una en un número impar, de acuerdo como$k$ es par o impar. De ahí$E(n) - O(n) = 0$, a menos que$n = \dfrac{1}{2}(3k \pm k)$, cuándo$E(n) - O(n) = (-1)^k$. Esto da el teorema de Euler.

Ahora, desde

$\sum p(n) x^n (1 - x - x^2 + x^5 + x^7 - x^{12} - \cdot\cdot\cdot) = 1$

obtenemos una relación de recurrencia para$p(n)$, a saber

$p(n) = p(n - 1) + p(n - 2) - p(n - 5) - p(n - 7) + p(n - 12) + \cdot\cdot\cdot.$