3.2: Una Solución Particular de ax+by = c

Última actualización
Guardar como PDF

Page ID: 111491

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Otra forma interesante de codificar los cálculos realizados en las ecuaciones 3.1 y 3.2 es a través de matrices.

\[\begin{pmatrix} {r_{i-1}}\\ {r_{i}} \end{pmatrix} = \begin{pmatrix} {q_{1}}&{1}\\ {1}&{0} \end{pmatrix} \begin{pmatrix} {r_{i}}\\ {r_{i+1}} \end{pmatrix}\]

Denote la matriz en esta ecuación por$Q_{i}$. Su determinante es igual$-1$, y así es invertible. De hecho,

\[\begin{array} {ccc} {Q_{i} = \begin{pmatrix} {q_{i}}&{1}\\ {1}&{0} \end{pmatrix}}&{and}&{Q_{i}^{-1} = \begin{pmatrix} {0}&{1}\\ {1}&{-q_{i}} \end{pmatrix}} \end{array}\]

Estas matrices$Q_{i}$ son muy interesantes. Los usaremos nuevamente para estudiar la teoría de las fracciones continuas en el Capítulo 6. Por ahora, como veremos en el Teorema 3.4, nos dan un algoritmo explícito para encontrar una solución a la ecuación$r_{1}x+r_{2}y = r \gcd(r_{1}, r_{2})$. Tenga en cuenta que del Lema de Bezout (Lemma 2.5), ya sabemos que esto tiene una solución. Pero el siguiente resultado nos da una forma sencilla de calcular realmente una solución. En lo que sigue$X_{ij}$ significa la$(i,j)$ entrada de la matriz$X$.

Teorema 3.4

Dar$r_{1}$ y$r_{2}$, una solución para$x$ y$y$ de$r_{1}x+r_{2}y = r \gcd(r_{1},r_{2})$ es dada por

\[\begin{array}{ccc} {x = r(Q_{n-1}^{-1} \cdots Q_{2}^{-1})_{2,1}}&{and}&{x = r(Q_{n-1}^{-1} \cdots Q_{2}^{-1})_{2,2}} \nonumber \end{array}\]

Prueba

Dejar$r_{i},q_{i}$, y$Q_{i}$ definirse como arriba, y establecer$r_{n+1} = 0$. A partir de la ecuación 3.4, tenemos

\[\begin{pmatrix} {r_{i}}\\ {r_{i+1}} \end{pmatrix} = Q_{i}^{-1} \begin{pmatrix} {r_{i-1}}\\ {r_{i}} \end{pmatrix} \Rightarrow r \begin{pmatrix} {r_{n-1}}\\ {r_{n}} \end{pmatrix} = r Q_{n-1}^{-1} \cdots Q_{2}^{-1} \begin{pmatrix} {r_{1}}\\ {r_{2}} \end{pmatrix} \nonumber\]

Observe eso$r_{n+1} = 0$ y así$\gcd (r_{1},r_{2} = r_{n}$ y

\[\begin{pmatrix} {r_{n-1}}\\ {r_{n}} \end{pmatrix} = \begin{pmatrix} {x_{n-1}}&{y_{n-1}}\\ {x_{n}}&{y_{n}} \end{pmatrix} \begin{pmatrix} {r_{1}}\\ {r_{2}} \end{pmatrix}\]

Las igualdades siguen de inmediato.

En la práctica, en lugar de multiplicar todas estas matrices, puede ser más conveniente resolver la ecuación 3.1 o 3.2 “hacia atrás”, según va la expresión. Esto se puede hacer de la siguiente manera. Empezar con

\[\gcd(r_{1}, r_{2}) = r_{n} = r_{n-2}-r_{n-1}q_{n-1} \nonumber\]

que se desprende de la ecuación 3.1. La línea por encima de ella en esa misma ecuación da$r_{n-1} = r_{n-3}-r_{n-2}q_{n-2}$. Usa esto para eliminar$r_{n-1}$ a favor de$r_{n-2}$ y$r_{n-3}$. Entonces,

\[\gcd(r_{1}, r_{2}) = r_{n} = r_{n-2}-(r_{n-3}-r_{n-2} q_{n-2}) q_{n-1} \nonumber\]

\[= r_{n-2} (1+q_{n-1}q_{n-2})+r_{n-3}(-q_{n-1}) \nonumber\]

Este cálculo se puede hacer aún más eficientemente empleando de nuevo la notación de la ecuación 3.2.

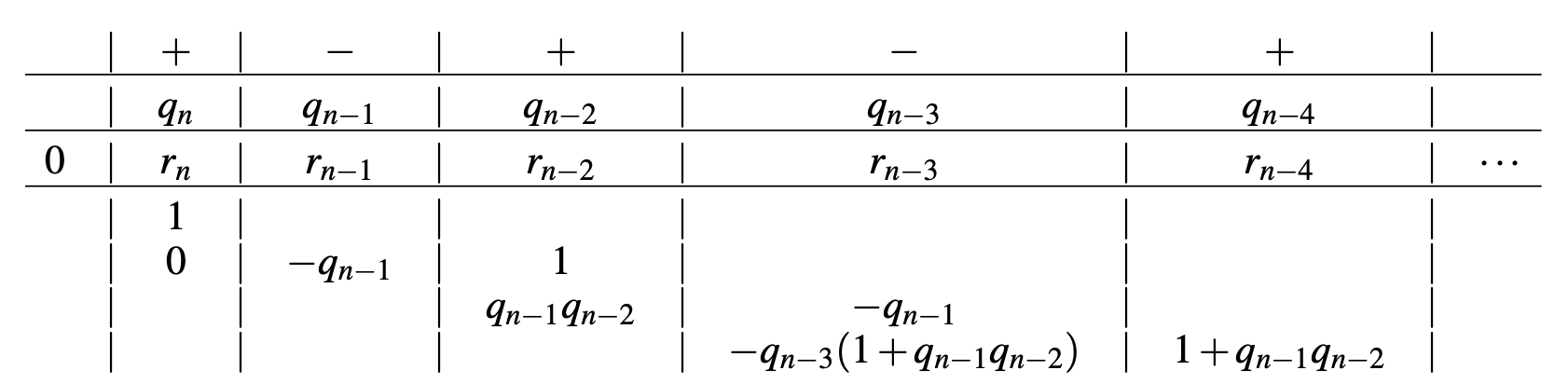
$Screen Shot 2021-04-21 a las 4.13.22 PM.png$

(Los signos agregados en la primera línea en este esquema sirven únicamente para hacer un seguimiento de los signos de los coeficientes en las líneas tres e inferiores). Aplicando esto al ejemplo da

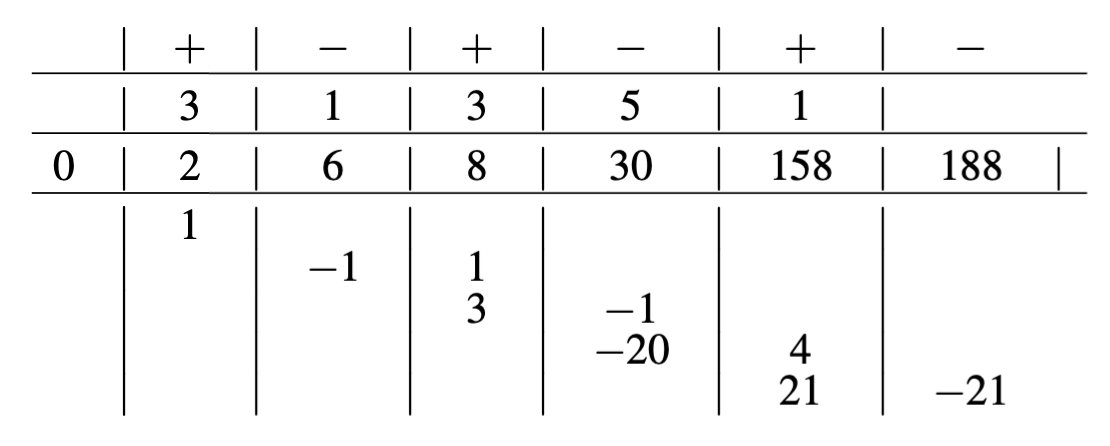
$Screen Shot 2021-04-21 a las 4.14.11 PM.png$

Sumando las dos últimas líneas da eso$2 = 158(25) + 188(-21)$.