3.4: La Solución General de ax+by = c

Última actualización
Guardar como PDF

Page ID: 111483

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Definición 3.8

Dejar$r_{1}$ y$r_{2}$ ser dado. La ecuación$r_{1}x + r_{2}y = 0$ se llama homogénea. La ecuación$r_{1}x + r_{2}y = c$ cuando$c \ne 0$ se llama no homogénea. Una solución arbitraria de la ecuación no homogénea se llama solución particular. Por solución general, nos referimos al conjunto de todas las soluciones posibles de la ecuación completa (no homogénea).

Es útil tener alguna intuición geométrica relevante para la ecuación$r_{1}x + r_{2}y = c$. En$\mathbb{R}^2$, nos fijamos$\vec{r} = (r_{1}, r_{2}), \vec{x} = (x, y)$, etcétera. El producto interno estándar está escrito como$(\cdot, \cdot)$. El conjunto de puntos para$\mathbb{R}^2$ satisfacer la ecuación no homogénea anterior se encuentra así en la línea$m \subset \mathbb{R}^2$ dada por$(\vec{r}, \vec{x}) = c$.

Esta línea es ortogonal al vector$\vec{r}$ y su distancia al origen (medida a lo largo del vector$\vec{r}$) es igual$\frac{|c|}{\sqrt{(\vec{r}, \vec{r})}}$. La situación se ilustra en la Figura 7.

Es un resultado estándar del álgebra lineal que el problema de encontrar todas las soluciones de una ecuación no homogénea se reduce a encontrar una solución de la ecuación no homogénea, y encontrar la solución general de la ecuación homogénea.

Lema 3.9

Dejar$(x^{(0)}, y^{(0)})$ ser una solución particular de$r_{1}x+r_{2}y = c$. La solución general de la ecuación no homogénea viene dada por$(x^{(0)}+z_{1}, y^{(0)}+z_{2})$ donde$(z_{1}, z_{2})$ está la solución general de la ecuación homogénea$r_{1}x+ r_{2}y = 0$.

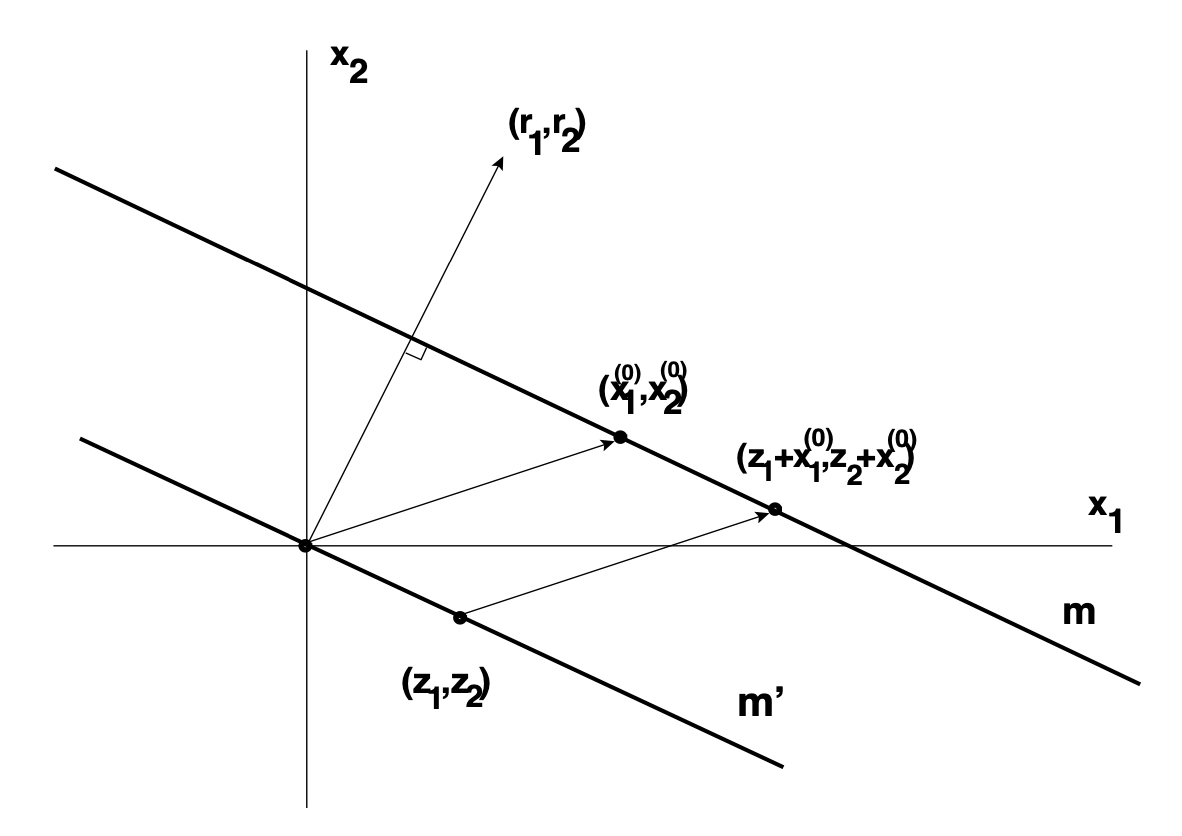
$Screen Shot 2021-04-23 a las 3.40.29 PM.png$

Figura 7. La solución general de la ecuación no homogénea$(\vec{r}, \vec{x})= c$ en$\mathbb{R}^2$.

Prueba: Que$(x^{(0)}, y^{(0)})$ sea esa solución en particular. Que$m$ sea la línea dada por$(\vec{r}, \vec{x})= c$. Traduce$m$ sobre el vector$(-x^{(0)}, -y^{(0)})$ para obtener la línea$m'$. Entonces un punto entero en la línea$m'$ es una solución$(z_{1}, z_{2})$ de la ecuación homogénea si y solo si$(x^{(0)}+z_{1}, y^{(0)}+z_{2})$ on$m$ es también un punto entero (ver Figura 7).

El lema de Be ́zout dice que$r_{1}x + r_{2}y = c$ tiene una solución si y solo si$\gcd (r_{1}, r_{2}) | c$. El teorema 3.4 da una solución particular de esa ecuación (a través del algoritmo euclidiano). Al juntar esos resultados y la Proposición 3.5, nos da nuestro resultado final.

Corolario 3.10

Dada$r_{1}, r_{2}$, y$c$, la solución general de la ecuación$r_{1}x+r_{2}y = c$, donde$\gcd(r_{1}, r_{2}) | c$, es la suma de la solución particular del Teorema 3.4 y la solución general$r_{1} x+r_{2} y = 0$ de la Proposición 3.5.