4.5: Serie Dirichlet y Lambert

Vamos a echar un vistazo rápido a algunas series interesantes sin preocuparnos demasiado por su convergencia, porque en última instancia nos interesan las continuaciones analíticas que subyacen a estas series. Para ello, basta con que haya convergencia en cualquier región abierta no vacía del plano complejo.

Definición 4.18

Dejar\(f, g\), y\(F\) ser funciones aritméticas (ver Definición 4.1). Definir la convolución de Dirichlet de\(f\) y\(g\), denotada por\(f \star g\), como

\[(f \ast g)(n) \equiv \sum_{ab=n} f(a)g(b) \nonumber\]

Esta convolución es una herramienta muy práctica. Similar a la convolución habitual de secuencias, se puede pensar en ella como una especie de multiplicación. Vale la pena definir primero algunas funciones teóricas de números estándar.

Definición 4.19

Utilizamos la siguiente notación para ciertas secuencias estándar. La secuencia\(\epsilon (n\) es\(1\) if\(n = 1\) and otherwise returns\(0\),\(\textbf{1} (n)\) always returns\(1\), y\(I(n)\) returns\(n (I(n) = n)\).

La función\(\epsilon\) actúa como la identidad de la convolución. Efectivamente,\((\epsilon \ast f)(n) = \sum_{ab=n} \epsilon(a) f(b) = f(n)\).

Obsérvese que\(I(n)\) es la identidad como una función, pero no debe confundirse con la identidad de la convolución\((\epsilon)\). En otras palabras,\(I(n) = n\) pero\(I \ast f \ne f\).

Ahora podemos hacer algunas cosas muy interesantes de las que lamentablemente podemos dar pero algunos ejemplos. Como primer ejemplo, reformulamos la inversión de Mo ̈bius del Teorema 4.14 de la siguiente manera:

\[F = \textbf{1} \ast f \Leftrightarrow f = \mu \ast F \nonumber\]

Esto lleva al siguiente ejemplo. La primera de las siguientes igualaciones se mantiene por Lema 4.15, la segunda se desprende de la inversión de Mobius.

\[I = \textbf{1} \ast \varphi \Leftrightarrow \varphi = \mu \ast I \nonumber\]

Y el mejor de estos ejemplos se obtiene sustituyendo la identidad\(\epsilon\) por\(F\) en la ecuación (4.5):

\[\epsilon = \textbf{1} \ast f \Leftrightarrow f = \mu \ast \epsilon = \mu \nonumber\]

Así\(\mu\) es la convolución inversa de la secuencia\((1,1,1 \cdots)\). Esto inmediatamente conduce a una expresión inesperada para\(1/ \zeta (s)\) de la ecuación (4.8).

Definición 4.20

Let\(f(n)\) es una función aritmética (o secuencia). Una serie de Dirichlet es una serie de la forma\(F(s) = \sum_{n=1} f(n) n^{-s}\). Del mismo modo, una serie Lambert es una serie de la forma\(F(x) = \sum_{n=1} f(n) \frac{x^n}{1-x^n}\)

El primer ejemplo de una serie de Dirichlet es —por supuesto— la función zeta de Riemann de la Definición 2.19,\(\zeta(s) = \sum \textbf{1} (n) n^{-s}\).

Teorema 4.21

Para el producto de dos series de Dirichlet contamos con

\[(\sum_{n=1} f(n)n^{-s})(\sum_{n=1} g(n)n^{-s}) = \sum_{n=1}^{\infty} (f \ast g) (n) n^{-s} \nonumber\]

Prueba

Esto se desprende fácilmente de la reordenación de los términos en el producto:

\[\sum_{a,b \ge 1}^{\infty} \frac{f(a) g(b)}{(ab)^s} = \sum_{n=1}^{\infty}(\sum_{n=1}^{\infty} f(a)g(b)) n^{-s} \nonumber\]

Recopilamos los términos con\(ab = n\).

Dado que\(\frac{\zeta (s)}{\zeta(s)} = 1\), la ecuación (4.7) y el lema implican inmediatamente que

\[\frac{1}{\zeta (s)} =\sum_{n \ge 1} \frac{\mu(n)}{n^s} \nonumber\]

Recordemos del Capítulo 2 que una de las principales preocupaciones de la teoría de números es la ubicación de los ceros no reales de\(\zeta\). En juego está Conjetura 2.22 que establece que todos sus ceros no reales están en la línea\(Re s = 1/2\). La definición original de la función zeta es como una serie que es absolutamente convergente por\(Re s > 1\) solo. Por lo tanto, es importante establecer que la continuación analítica de\(\zeta\) es válida para\(Re s \le 1\). El siguiente resultado sirve como una primera indicación que de hecho se\(\zeta (s)\) puede continuar para los valores\(Re s \le 1\).

Teorema 4.22

\(\zeta\)Sea la función zeta de Riemann y\(\sigma_{k}\) como en la Definición 4.4, entonces

\[\zeta (s-k) \zeta (s) =\sum_{n=1}^{\infty} \frac{\sigma_{k} (n)}{n^s} \nonumber\]

Prueba

\[\zeta (s-k) \zeta (s) = \sum_{a \ge 1} a^{-s} \sum_{b \ge 1} b^{k} b^{-s} = \sum_{n \ge 1} n^{-s} \sum_{b|n} b^k \nonumber\]

Lema 4.23

Una serie Lambert puede resumirse de la siguiente manera:

\[\sum_{n=1}^{\infty} f(n) \frac{x^n}{1-x^n} = \sum_{n=1}^{\infty} (\textbf{1} \ast f) (n) x^{n} \nonumber\]

Prueba

Primero use eso

\[\frac{x^b}{1-x^b} = \sum_{a=1}^{\infty} x^{ab} \nonumber\]

Esto da que

\[\sum_{n=1}^{\infty} f(b) \frac{x^b}{1-x^b} = \sum_{b=1}^{\infty} \sum_{a=1}^{\infty} f(b) x^{ab} \nonumber\]

Ahora establece\(n = ab\) y recoge términos. Observando que (\ textbf {1}\ ast f) (b) =\ sum_ {b\ nmid n} f (b)\) arroja el resultado.

Corolario 4.24

La siguiente igualdad sostiene

\[\sum_{n \ge 1} \varphi (n) \frac{x^n}{1-x^n} = \frac{x}{(1-x)^2} \nonumber\]

Prueba

Tenemos

\[\sum_{n \ge 1} \varphi (n) \frac{x^n}{1-x^n} = \sum_{n \ge 1} (\textbf{1} \ast \varphi) (n) x^n = \sum_{n \ge 1} I(n) x^n \nonumber\]

La primera igualdad se desprende de Lemma 4.23 y la segunda de Lemma 4.15. La última suma se puede calcular como\(x \frac{d}{dx} (1-x)^{-1}\) lo que da la expresión deseada.

El último resultado es de importancia en el estudio de los sistemas dinámicos. En la figura 8, el mapa\(f_{t}\) se construye truncando el\(x \rightarrow 2x\) mod de mapa\(1\) para\(t \in [0, 1]\). El corolario 4.24 puede utilizarse para mostrar que el conjunto de\(t\) para el que\(f_{t}\) no tiene órbita periódica tiene medida (“longitud”) cero [24, 25], aunque ese conjunto sea incontable.

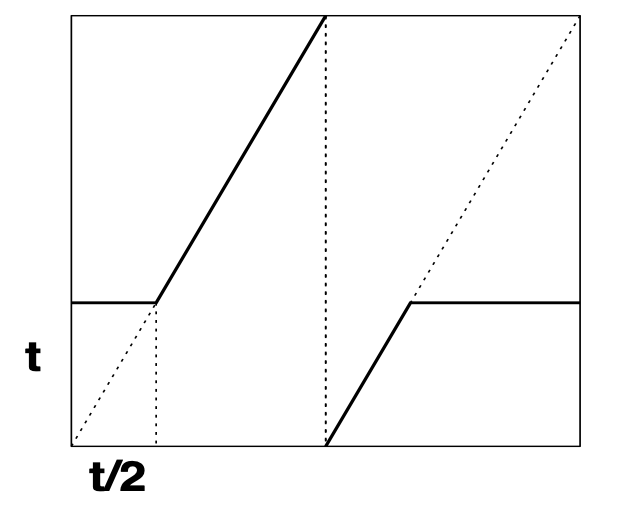
Figura 8. Una familia\(f_{t}\) de mapas de un parámetro del círculo a sí mismo. Para cada\(t \in [0, 1]\) el mapa\(f_{t}\) se construye truncando el\(x \rightarrow 2x\) mod de mapa\(1\) como se indica en esta figura.