18.5: Explicando las relaciones entre actores en una red

En la sección anterior analizamos algunas herramientas para hipótesis sobre actores individuales incrustados en redes. Modelos como estos son muy útiles para examinar las relaciones entre los atributos relacionales y no relacionales de los individuos.

Una de las formas más distintivas en las que se ha aplicado el análisis estadístico a los datos de las redes sociales es enfocarse en predecir las relaciones de los actores, en lugar de sus atributos. En lugar de construir un modelo estadístico para predecir el grado de salida de cada actor, podríamos, en cambio, predecir si había un vínculo de cada actor con el otro actor. En lugar de explicar la varianza en las personas individuales, podríamos enfocarnos en explicar la variación en las relaciones.

En esta sección final, veremos varios modelos estadísticos que buscan predecir la presencia o ausencia (o fuerza) de un empate entre dos actores. Modelos como este se centran directamente en una cuestión muy sociológica: ¿qué factores afectan la probabilidad de que dos individuos tengan una relación?

Un predictor obvio, pero muy importante, de si es probable que dos actores estén conectados es su similitud o cercanía. En muchas teorías sociológicas, se predice que dos actores que comparten algún atributo tendrán más probabilidades de formar lazos sociales que dos actores que no lo hacen. Esta hipótesis de “homofilia” está en el centro de muchas teorías de diferenciación, solidaridad y conflicto. A menudo se plantea la hipótesis de que dos actores que están más cerca de uno en una red tienen más probabilidades de formar vínculos; es probable que dos actores que comparten atributos estén a distancias más cercanas entre sí en las redes.

Varios de los modelos a continuación exploran la homofilia y cercanía para predecir si los actores tienen vínculos, o están cerca unos de otros. El último modelo que veremos en el modelo “P1" también busca explicar las relaciones. El modelo P1 intenta predecir si no existe una relación, una relación asimétrica o un vínculo recíproco entre pares de actores. Sin embargo, en lugar de usar atributos o cercanía como predictores, el modelo P1 se enfoca en las propiedades básicas de la red de cada actor y de la red en su conjunto (in-degree, out-degree, reciprocidad global). Este tipo de modelo —un modelo de probabilidad para la presencia/ausencia de cada relación posible en una gráfica en función de las estructuras de red— es una de las principales áreas continuas de desarrollo en los métodos de redes sociales.

Hipótesis sobre las relaciones dentro/entre grupos

Una de las observaciones sociológicas más comunes es que “las aves de una pluma acuden juntas”. La noción de que la similitud (u homofilia) aumenta la probabilidad de la formación de vínculos sociales es central en la mayoría de las teorías sociológicas. La hipótesis de la homofilia puede leerse para estar haciendo una predicción sobre las redes sociales. Se sugiere que si dos actores son similares de alguna manera, es más probable que haya lazos de red entre ellos. Si nos fijamos en una red social que contiene dos tipos de actores, la densidad de vínculos debería ser mayor dentro de cada grupo que entre grupos.

Herramientas>Hipótesis de Prueba>Diádica Mixta/Nodal>Atributos Categóricos>Conteo Conjunto Proporciona una prueba de que la densidad de lazos dentro y entre dos grupos difiere de lo que esperaríamos si los lazos se distribuyeran al azar a través de todos los pares de nodos.

El procedimiento toma una gráfica binaria y una partición (es decir, un vector que clasifica cada nodo como que está en un grupo u otro), y permuta y bloquea los datos. Si no hubo asociación entre compartir el mismo atributo (es decir, estar en el mismo bloque) y la probabilidad de un empate entre dos actores, podemos predecir el número de vínculos que deberían estar presentes en cada uno de los cuatro bloques de la gráfica (es decir: grupo 1 por grupo 1; grupo 1 por grupo 2; grupo 2 por grupo 1; y grupo 2 por grupo 2). Estas cuatro “frecuencias esperadas” se pueden comparar entonces con las cuatro “frecuencias observadas”. La lógica es exactamente la misma que la prueba de independencia de Chi-cuadrado de Pearson: podemos generar una “estadística de prueba” que muestre hasta qué punto la tabla 2 por 2 se aparta de la “independencia” o de la “no asociación”.

Sin embargo, para probar la significancia inferencial de las desviaciones de la aleatoriedad, no podemos confiar en tablas estadísticas estándar. En cambio, se calcula una gran cantidad de gráficas aleatorias con la misma densidad general y particiones del mismo tamaño. Luego se puede calcular la distribución muestral de las diferencias entre las observadas y las esperadas para gráficas aleatorias, y se utiliza para evaluar la probabilidad de que nuestra gráfica observada pudiera ser el resultado de un ensayo aleatorio de una población donde no hubo asociación entre la pertenencia al grupo y la probabilidad de una relación.

Para ilustrar, si dos grandes donantes políticos contribuyeron del mismo lado de las campañas políticas (a través de 48 campañas de iniciativa), los codificamos “1" como que tienen empate o relación, de lo contrario, los codificamos cero. Hemos dividido a nuestros grandes donantes políticos en campañas de iniciativa de California en dos grupos: los que están afiliados a “trabajadores” (por ejemplo, los sindicatos, el partido Demócrata), y los que no lo son.

Anticiparíamos que dos grupos que representan los intereses de los trabajadores tendrían más probabilidades de compartir el lazo de estar en coaliciones para apoyar iniciativas que dos grupos dibujados al azar. La Figura 18.16 muestra los resultados de Herramientas>Hipótesis de prueba>Diádica Mixta/Nodal>Atributos Categóricos> Conteo conjunto aplicado a este problema.

Figura 18.16: Prueba para diferencias de dos grupos en la densidad de amarre

El vector de partición (variable de identificación de grupo) se codificó originalmente como cero para donantes no trabajadores y uno para donantes de trabajadores. Estos han sido re-etiquetados en la salida como uno y dos. Hemos utilizado el valor predeterminado de 10,000 gráficas aleatorias para generar la distribución de muestreo para las diferencias de grupo.

La primera fila, etiquetada como “1-1" nos dice que, bajo la hipótesis nula de que los vínculos se distribuyen aleatoriamente entre todos los actores (es decir, el grupo no hace diferencia), nosotros haríamos esperar 30.356 vínculos que estén presentes en el bloque de no trabajador a no trabajador. En realidad observamos 18 empates en este bloque, 12 menos de lo que se esperaría. Una diferencia negativa esta grande ocurrió solo 2.8% del tiempo en gráficas donde los lazos se distribuyeron aleatoriamente. Es claro que tenemos una desviación de la aleatoriedad dentro del bloque “no trabajador”. Pero la diferencia no apoya la homofilia —sugiere todo lo contrario; los vínculos entre actores que comparten el atributo de no representar a los trabajadores son menos probables que aleatorios, más que más probables.

La segunda fila, etiquetada como “1-2" no muestra diferencia significativa entre el número de vínculos observados entre grupos de trabajadores y no trabajadores y lo que sucedería por casualidad bajo la hipótesis nula de no efecto de la pertenencia a grupos compartidos sobre la densidad de vínculos.

La tercera fila, etiquetada como “2-2" Una diferencia tan grande indica que el recuento observado de vínculos entre los grupos de interés que representan a los trabajadores (21) es mucho mayor que esperado por casualidad (5.3) casi nunca se observaría si la hipótesis nula de no efecto grupal sobre la probabilidad de vínculos fuera cierta.

Quizás nuestro resultado no apoya la teoría de la homofilia porque el grupo “no trabajador” no es realmente como grupo social en absoluto, solo una colección residual de diversos intereses. Uso de Herramientas>Hipótesis de Prueba>Diádica Mixta/Nodal>Atributos Categóricos>Tabla de Contingencia Relacional Análisis podemos ampliar el número de grupos para proporcionar una mejor prueba. Esta vez, categorizemos a los donantes políticos como representantes de “otros”, “capitalistas” o “trabajadores”. Los resultados de esta prueba se muestran como figura 18.17.

Figura 18.17: Prueba para diferencias de tres grupos en la densidad de amarre

El “otro” grupo ha sido re-etiquetado como “1", el grupo “capitalista” re-etiquetado como “2", y el grupo “obrero” re-etiquetado como “3". Hay 87 lazos totales en la gráfica, con las frecuencias observadas mostradas (“Frecuencias clasificadas cruzadas).

Podemos ver que las frecuencias observadas difieren de los “Valores Esperados Bajo Modelo de Independencia”. Las magnitudes de la sobre-representación y la subrepresentación se muestran como “Observado/Esperado”. Observamos que las tres celdas diagonales (es decir, los lazos dentro de los grupos) ahora muestran homofilia, mayor que la densidad aleatoria.

Se calcula un estadístico chi-cuadrado de Pearson (74.217). Y, se nos muestran los conteos promedio de empate en cada celda que ocurrieron en los 10,000 ensayos aleatorios. Finalmente, observamos que p < 0.0002. Es decir, la desviación de los lazos de la aleatoriedad es tan grande que ocurriría sólo muy raramente si el modelo de no asociación fuera cierto.

Modelos de Homofilía

El resultado en la sección anterior parece apoyar la homofilia (que podemos ver al observar dónde ocurren las desviaciones de la independencia. La prueba estadística, sin embargo, es solo una prueba global de diferencia con la distribución aleatoria. Las herramientas de rutina>Hipótesis de prueba>Diádica Mixta/Nodal>Atributos Categóricos>Modelos de Densidad proporciona pruebas específicas de algunos modelos de homofilia bastante específicos.

La noción menos específica de cómo los miembros de los grupos se relacionan con los miembros de otros grupos es simplemente que los grupos difieren. Los miembros de un grupo pueden preferir tener vínculos solo dentro de su grupo; los miembros de otro grupo pueden preferir tener vínculos solo fuera de su grupo.

La opción de Modelo de Bloques Estructurales de Herramientas>Hipótesis de Prueba>Diadica/Nodal>Atributos Categóricos>Modelos de Densidad ANOVA proporciona una prueba de que los patrones de vínculos dentro y entre grupos difieren entre grupos, pero no especifica de qué manera pueden diferir. La Figura 18.18 muestra los resultados de ajustar este modelo a los datos sobre fuertes lazos de coalición (compartiendo 4 o más campañas) entre “otros” grupos de interés “capitalistas” y “obreros”.

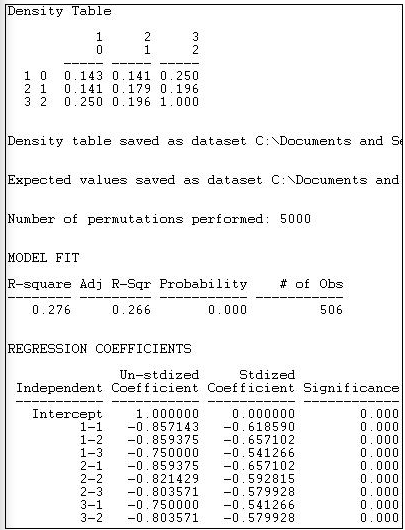
Figura 18.18: Modelo de bloques estructurales de diferencias en la densidad de amarre de grupo

Primero se muestra la tabla de densidad observada. Los miembros del “otro” grupo tienen una baja probabilidad de estar amarrados entre sí (0.143) o a “capitalistas” (0.143), pero vínculos algo más fuertes con los “trabajadores” (0.250). Sólo los “trabajadores” (categoría 2, fila 3) muestran fuertes tendencias hacia los vínculos dentro del grupo.

A continuación, se ajusta un modelo de regresión a los datos. La presencia o ausencia de un empate entre cada par de actores se retrocede sobre un conjunto de variables ficticias que representan cada una de las celdas de la tabla de bloques de 3 por 3. En esta regresión, se utiliza como categoría de referencia el último bloque (i.e. 3-3). En nuestro ejemplo, las diferencias entre bloques explican 27.6% de la varianza en la presencia o ausencia de vínculos por pares. La probabilidad de un empate entre dos actores, ambos de los cuales están en el bloque “trabajadores” (bloque 3) es de 1.000. La probabilidad en el bloque que describe vínculos entre “otros” y “otros” actores (bloque 1-1) es .857 menor que esta.

La significancia estadística de este modelo no puede evaluarse adecuadamente utilizando fórmulas estándar para observaciones independientes. En cambio, se han realizado 5000 ensayos con permutaciones aleatorias de la presencia y ausencia de vínculos entre pares de actores, y se calcularon errores estándar estimados a partir de la distribución de muestreo simulada resultante.

Una noción mucho más restringida de diferencias de grupo se denomina el modelo de Homofilía Constante en Herramientas>Hipótesis de Prueba>Diadica/Nodal>Atributos Categóricos>Modelos de Densidad ANOVA . Este modelo propone que todos los grupos pueden tener preferencia por los vínculos dentro del grupo, pero que la fuerza de la preferencia es la misma dentro de todos los grupos. Los resultados de ajustar este modelo a los datos se muestran en la figura 18.19.

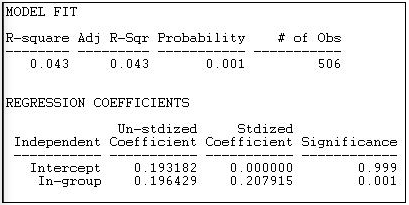
Figura 18.19: Modelo de bloques de Homofilia Constante de diferencias en la densidad de ligadura de grupo

Dado lo que observamos al observar directamente las densidades de bloque (mostrado en la figura 18.18), no es sorprendente que el modelo de homofilia constante no se ajuste a estos datos bien. Sabemos que dos de los grupos (“otros” y “capitalistas”) no tienen aparente tendencia a la homofilia —y eso difiere mucho del grupo “obrero”. El modelo de bloques de diferencias de grupo solo representa 4.3% de la varianza en los vínculos por pares; sin embargo, los ensayos de permutación sugieren que este no es un resultado aleatorio (p = 0.001).

Este modelo solo tiene dos parámetros, ya que la hipótesis es proponer una diferencia simple entre las celdas diagonales (los lazos dentro del grupo 1-1, 2-2 y 3-3) y todas otras celdas. La hipótesis es que las densidades dentro de estas dos particiones son las mismas. Vemos que la densidad promedio estimada de empate de parejas que no están en el mismo grupo es de 0.193 —existe una probabilidad de 19.3% de que díadas heterogéneas tengan empate. Si los miembros de la díada son del mismo grupo, la probabilidad de que compartan empate es 0.196 mayor, o 0.389.

Entonces, aunque el modelo de homofilia constante no predice en absoluto bien los lazos del individuo, existe un notable efecto de homofilia general.

Señalamos que la fuerte tendencia hacia los vínculos dentro del grupo parece describir solo al grupo “obrero”. Un tercer modelo de bloque, etiquetado Homofilia Variable por Herramientas>Hipótesis de prueba>Diádica Mixta/ Nodal>Atributos Categóricos>Modelos de Densidad ANOVA prueba el modelo que cada diagonal celda (es decir, los vínculos dentro del grupo 1, dentro del grupo 2 y dentro del grupo 3) difieren de todos los vínculos que no están dentro del grupo. La Figura 18.20 muestra los resultados.

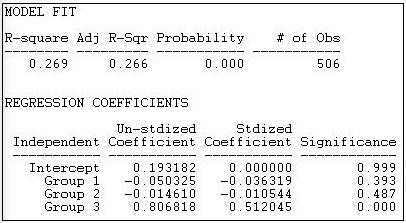
Figura 18.20: Modelo de bloques de homofilia variable de diferencias en la densidad de ligadura de grupo

Este modelo se ajusta mucho mejor a los datos (R-cuadrado = 0.269, con p < 0.000) que el modelo de homofilia constante. También se ajusta a los datos casi tan bien como al modelo de bloques estructurales no restringidos (Figura 18.18), pero es más simple.

Aquí, la intercepción es la probabilidad de que haya un empate diádico entre dos miembros cualesquiera de diferentes grupos (0.193). Vemos que la probabilidad de vínculos dentro de grupo entre el grupo 1 (“otros”) es en realidad 0.05 menor que esto (pero no significativamente diferente). Dentro de grupo, los vínculos entre los grupos de interés capitalistas (grupo 2) son muy poco menos comunes (-0.01) que los vínculos de grupo heterogéneos (nuevamente, no significativos). Sin embargo, los vínculos entre grupos de interés que representan a los trabajadores (grupo 3) son dramáticamente más prevalentes (0.81) que los vínculos dentro de pares heterogéneos

En nuestro ejemplo, notamos que un grupo parece mostrar lazos dentro del grupo, y otros no. Una forma de pensar sobre este patrón es un modelo de bloques de “núcleo-periferia”. Hay una forma fuerte, y una forma más relajada de la estructura núcleo-periferia.

El modelo Core-periferia 1 supone que hay un núcleo altamente organizado (muchos lazos dentro del grupo), pero que hay pocos otros vínculos, ya sea entre miembros de la periferia, o entre miembros del núcleo y miembros de la periferia. La Figura 18.21 muestra los resultados de ajustar este modelo de bloques a los datos de donantes de California.

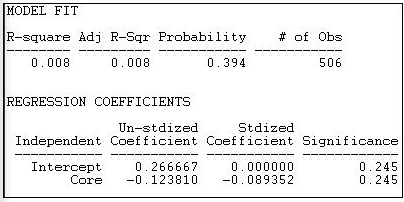
Figura 18.21: Modelo de bloque núcleo-periferia “fuerte” de donantes políticos de California

Es claro que este modelo no hace un buen trabajo al describir el patrón de vínculos dentro y entre grupos. El R-cuadrado es muy bajo (0.008), y los resultados tan pequeños se producirían 39.4% del tiempo en ensayos a partir de datos permutados aleatoriamente. Los coeficientes de regresión (no significativos) muestran densidad (o probabilidad de empate entre dos actores aleatorios) en la periferia como .27, y la densidad en el “Núcleo” como 0.12 menos que esto. Dado que el “núcleo” es, por definición, el área máximamente densa, parece que la salida en la versión 6.8.5 puede estar mal etiquetada.

Core-Periphery 2 ofrece un modelo de bloque más relajado en el que el núcleo permanece densamente atado dentro de sí mismo, pero se le permite tener lazos con la periferia. La periferia es, al máximo grado posible, un conjunto de casos sin vínculos dentro de su grupo. La Figura 18.22 muestra los resultados de este modelo para los donantes políticos de California.

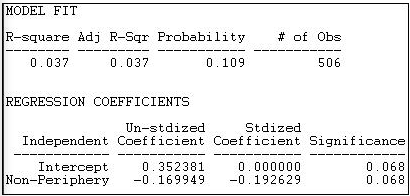
Figura 18.22: Modelo de bloque núcleo-periferia “relajado” de donantes políticos de California

El ajuste de este modelo es mejor (R-cuadrado = 0.037) pero aún muy pobre. Resultados tan fuertes se producirían alrededor del 11% del tiempo en ensayos a partir de datos permutados aleatoriamente. La densidad de intercepción (que interpretamos como la “no periferia”) es mayor (aproximadamente 35% de todos los lazos están presentes), y la probabilidad de empate entre dos casos en la periferia es .17 menor.

Hipótesis sobre similitud y distancia

La hipótesis de la homofilia a menudo se piensa en términos categóricos: ¿existe una tendencia a que los actores que son del mismo “tipo” se encuentren adyacentes (o cercanos) entre sí en la red?

Esta idea, sin embargo, puede generalizarse a atributos continuos: ¿hay una tendencia a que los actores que tienen atributos más similares se ubiquen más cerca unos de otros en una red?

UCINET Herramientas>Hipótesis de prueba>Diádica mixta? Nodal>Atributos continuos>La estadística de Moran/Geary proporciona dos medidas que abordan la cuestión de la” autocorrelación” entre las puntuaciones del actor en las medidas de nivel de intervalo de sus atributos y la distancia de red entre ellos. Las dos medidas (la I de Moran y la C de Geary) están adaptadas para el análisis de redes sociales desde sus orígenes en la geografía, donde se desarrollaron para medir hasta qué punto se relacionó la similitud de las características geográficas de dos lugares cualesquiera con la distancia espacial entre ellas.

Supongamos que nos interesaba si había una tendencia para que grupos de interés políticos que estaban “cercanos” entre sí gastaran cantidades similares de dinero. Podríamos suponer que los grupos de interés que son aliados frecuentes también pueden influir entre sí en términos de los niveles de recursos que aportan —que entre los aliados frecuentes surge una especie de norma de niveles esperados de contribución.

Usando información sobre las contribuciones de donantes muy grandes (que entregaron un total de $5,000,000) a al menos cuatro (de 48) iniciativas de boletas en California, podemos ilustrar la idea de autocorrelación de red.

Primero, creamos un archivo de atributos que contiene una columna que tiene la puntuación de atributo de cada nodo, en este caso, la cantidad de gastos totales por parte de los donantes.

Segundo, creamos un conjunto de datos matriciales que describe la “cercanía” de cada par de actores. Aquí hay varios enfoques alternativos. Una es usar una matriz de adyacencia (binaria). Ilustraremos esto codificando a dos donantes como adyacentes si aportaron fondos del mismo lado de al menos cuatro campañas (aquí, hemos construido adyacencia a partir de datos de “afiliación”; a menudo tenemos una medida directa de adyacencia, como un donante nombrando a otro como aliado). También podríamos usar una medida continua de la fuerza del vínculo entre actores como una medida de “cercanía”. Para ilustrar esto, utilizaremos una escala de la similitud de los perfiles de contribución de los donantes que va desde números negativos (indicando que dos donantes dieron dinero en lados opuestos de las iniciativas) hasta números positivos (indicando el número de veces que los donados en el mismo lado de las cuestiones. Uno puede imaginar fácilmente otros enfoques para indexar la cercanía de la red de los actores (por ejemplo, 1/distancia geodésica). Se puede utilizar cualquier matriz de “proximidad” que capte la cercanía por pares de actores (para algunas ideas, ver Herramientas>Similitudes y Herramientas>Disimilitudes y distancias ).

Las figuras 18.23 y 18.24 muestran los resultados de Herramientas>Hipótesis de Prueba>Diádica Mixta/Nodal>Atributos Continuos>Estadística Moran/Geary donde hemos examinado la autocorrelación de los niveles de gasto de actores utilizando la adyacencia como nuestra medida de distancia de red. Muy simple: ¿los actores que son adyacentes en la red tienden a dar cantidades similares de dinero? Se presentan dos estadísticas y alguna información relacionada (la estadística Moran en la Figura 18.23 y la estadística Geary en la Figura 18.24.

Figura 18.23: Autocorrelación Moran de los niveles de gasto por donantes políticos con adyacencia de red

El estadístico Moran “I” de autocorrelación (desarrollado originalmente para medir la autocorrelación espacial, pero utilizado aquí para medir la autocorrelación de red) oscila entre -1.0 ( correlación negativa perfecta) a través de 0 (sin correlación) a +1.0 (correlación positiva perfecta). Aquí vemos el valor de -0.119, lo que indica que existe una tendencia muy modesta a que los actores que están adyacentes difieran más en cuanto aportan que dos actores aleatorios. En todo caso, parece que los miembros de la coalición pueden variar más en sus niveles de contribución que los actores aleatorios — ¡otra hipótesis muerde el polvo!

El estadístico Moran (ver cualquier texto de geoestadística, o hacer una búsqueda en Google) se construye muy parecido a un coeficiente de correlación regular. Indiza el producto de las diferencias entre las puntuaciones de dos actores y la media, ponderada por la similitud del actor, es decir, una covarianza ponderada por la cercanía de los actores. Esta suma se toma en relación a varianza en las puntuaciones de todos los actores a partir de la media. La medida resultante, al igual que el coeficiente de correlación, es una relación de covarianza a varianza, y tiene una interpretación convencional.

Los ensayos de permutación se utilizan para crear una distribución de muestreo. En muchos ensayos (en nuestro ejemplo 1,000), las puntuaciones sobre el atributo (gasto, en este caso) se asignan aleatoriamente a los actores, y se calcula la estadística Moran. En estos ensayos aleatorios, el promedio observado de Moran es de -0.043, con una desviación estándar de .073. La diferencia entre lo que observamos (-0.119) y lo que se predice por asociación aleatoria (-0.043) es pequeña en relación con la variabilidad del muestreo. De hecho, 17.4% de todas las muestras de datos aleatorios mostraron correlaciones al menos tan grandes, mucho más que la tasa de error convencional del 5% aceptable.

La medida de correlación de Geary se calcula e interpreta de manera algo diferente. Los resultados se muestran en la Figura 18.24 para la asociación de niveles de gasto por adyacencia de red.

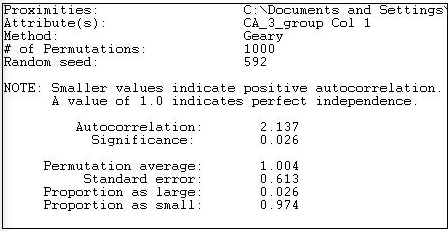
Figura 18.24: Autocorrelación geary de los niveles de gasto por donantes políticos con adyacencia de red

El estadístico Geary tiene un valor de 1.0 cuando no hay asociación. Los valores menores a 1.0 indican una asociación positiva (algo confusamente), los valores mayores a 1.0 indican una asociación negativa. Nuestro valor calculado de 2.137 indica autocorrelación negativa, tal como lo hizo el estadístico Moran. Sin embargo, a diferencia del estadístico Moran, el estadístico de Geary sugiere que la diferencia de nuestro resultado con el promedio de 1,000 ensayos aleatorios (1.004) es estadísticamente significativa (p = 0.026).

El estadístico Geary se describe a veces en la literatura geoestadística como más sensible a las diferencias “locales” que a las diferencias “globales”. El estadístico Geary C se construye examinando las diferencias entre las puntuaciones de cada par de actores y ponderando esto por su adyacencia. El estadístico Moran se construye observando las diferencias entre la puntuación de cada actor y la media, y ponderando los productos cruzados. La diferencia en el enfoque significa que la estadística de Geary está más enfocada en cómo son los diferentes miembros de cada par entre sí, una diferencia “local”; la estadística de Moran se enfoca más en cómo son los similares o diferentes que son cada par con respecto al promedio general, una diferencia “global”.

En datos donde el “paisaje” de valores muestra mucha variación, y distribución no normal, es probable que las dos medidas den impresiones algo diferentes acerca de los efectos de la adyacencia de la red en la similitud de atributos. Como siempre, no es que uno sea “correcto” y el otro “incorrecto”. Siempre es mejor computar ambos, a menos que tengas fuertes priores teóricos que sugieran que uno es superior para un propósito particular.

Las figuras 18.25 y 18.26 repiten el ejercicio anterior, pero con una diferencia. En estos dos ejemplos, medimos la cercanía de dos actores de la red en una escala continua. Aquí, hemos utilizado el número neto de campañas en las que cada par de actores estaban en la misma coalición como medida de cercanía. Otras medidas, como las distancias geodésicas, podrían usarse más comúnmente para datos de red verdaderos (en lugar de una red inferida de la afiliación).

Figura 18.25: Autocorrelación Moran de los niveles de gasto por donantes políticos con cercanía a la red

Usando una medida continua de cercanía de la red (en lugar de adyacencia) podríamos esperar una correlación más fuerte. La medida de Moran es ahora -0.145 (comparado con -0.119), y es significativa a p = 0.018. Existe una tendencia pequeña, pero significativa, para que los actores que son aliados “cercanos” den cantidades de dinero diferentes a las de dos actores elegidos al azar, una autocorrelación negativa de la red.

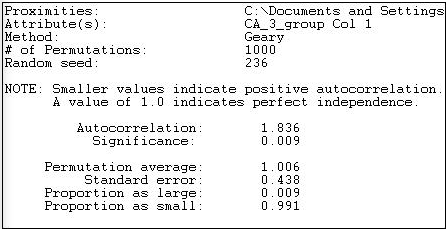
Figura 18.26: Autocorrelación Geary de los niveles de gasto por donantes políticos con cercanía a la red

La medida de Geary se ha vuelto ligeramente más pequeña en tamaño (1.836 versus 2.137) usando una medida continua de la distancia de la red. El resultado también indica una autocorrelación negativa, y una que rara vez ocurriría por casualidad si realmente no hubiera asociación entre distancia de red y gasto.

La probabilidad de un empate diádico: P1 de Leinhardt

Los enfoques que hemos estado examinando en esta sección analizan la relación entre los atributos del actor y su ubicación en una red. Antes de cerrar nuestra discusión sobre cómo se ha aplicado el análisis estadístico a los datos de la red, debemos mirar un enfoque que examine cómo los vínculos entre pares de actores se relacionan con atributos relacionales particularmente importantes de los actores, y con una característica más global de la gráfica.

Para cualquier par de actores en una gráfica dirigida, hay tres relaciones posibles: sin vínculos, un empate asimétrico, o un empate recíproco. Redes>P1 es un enfoque similar a la regresión que busca predecir la probabilidad de cada uno de estos tipos de relaciones para cada par de actores. Esto difiere un poco de los enfoques que hemos examinado hasta ahora que buscan predecir ya sea la presencia/ausencia de un empate, o la fuerza de un empate.

El modelo P1 (y su nuevo sucesor el modelo P*), buscan predecir las relaciones diádicas entre pares de actores usando atributos relacionales clave de cada actor, y de la gráfica en su conjunto. Esto difiere de la mayoría de los enfoques que hemos visto anteriormente, que se centran en los atributos individuales o relacionales del actor, pero no incluyen las características estructurales generales de la gráfica (al menos no explícitamente).

El modelo P1 consta de tres ecuaciones de predicción, diseñadas para predecir la probabilidad de una relación mutua (es decir, recíproca) (m _ij), una asimétrica relación (a _ij), o una relación nula (n _ij) entre actores. Las ecuaciones, tal y como afirman los autores de la UCINET son:

\[m_{ij} = \lambda_{ij} e^{\rho + 2 \theta + \alpha_i + \alpha_j + \hat{a}_i + \hat{a}_j}\]

\[a_{ij} = \lambda_{ij} e^{\theta + \alpha_i + \beta_j}\]

\[n_{ij} = \lambda_{ij}\]

La primera ecuación dice que la probabilidad de un empate recíproco entre dos actores es una función del grado de salida (o “expansividad”) de cada actor: alfa _i y alfa _j. También es una función de la densidad global de la red (theta). También es una función de la tendencia global en toda la red hacia la reciprocidad (rho). La ecuación también contiene constantes de escalado para cada actor del par (a _i y a _j), así como un parámetro de escala global (lambda).

La segunda ecuación describe la probabilidad de que dos actores estén conectados con una relación asimétrica. Esta probabilidad es una función de la densidad general de la red (theta), y la propensión de un actor de la pareja a enviar lazos (expansividad, o alfa), y la propensión del otro actor a recibir lazos (“atractivo” o beta).

La probabilidad de una relación nula (sin empate) entre dos actores es una “residual”. Es decir, si los lazos no son mutuos o asimétricos, deben ser nulos. Solo la constante de escalado “lambda” y ningún parámetro causal entran en la tercera ecuación.

La idea central aquí es que tratamos de entender las relaciones entre pares de actores como funciones de atributos relacionales individuales (tendencias individuales a enviar lazos, y recibirlos) así como características clave de la gráfica en la que están incrustados los dos actores (la densidad general y la tendencia general hacia la reciprocidad). Las versiones más recientes del modelo (P*, P2) incluyen características globales adicionales de la gráfica como las tendencias hacia la transitividad y la varianza entre actores en la propensión a enviar y recibir lazos.

La Figura 18.27 muestra los resultados de ajustar el modelo P1 a la red de información binaria Knoke.

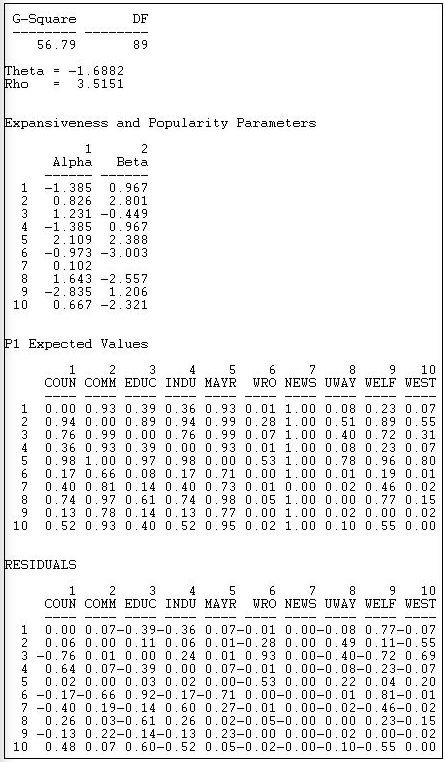
Figura 18.27: Resultados del análisis P1 de la red de información Knoke

Los aspectos técnicos de la estimación del modelo P1 son complicados y se utilizan métodos de máxima verosimilitud. Se proporciona un estadístico de maldad de ajuste de G-cuadrado (razón de verosimilitud chi-cuadrado), pero no tiene interpretación directa ni prueba de significancia.

Se dan dos parámetros descriptivos para las propiedades de red global:

• \(\theta\) = -1.6882 refers to the effect of the global density of the network on the probability of reciprocated or asymmetric ties between pairs of actors.
• \(\rho\) = 3.5151 refers to the effect of the overall amount of reciprocity in the global network on the probability of a reciprocated tie between any pair of actors.

Se dan dos parámetros descriptivos para cada actor (estos se estiman a través de todas las relaciones de pares de cada actor):

\(\alpha\) ("expansiveness") refers to the effect of each actor's out-degree on the probability that they will have reciprocated or asymmetric ties with other actors. We see, for example, that the Mayor (actor 5) is a relatively "expansive" actor.

\(\beta\) ("attractiveness") refers to the effect of each actor's in-degree on the probability that they will have a reciprocated or asymmetric relation with other actors. We see here, for example, that the welfare rights organization (actor 6) is very likely to be shunned.

Usando las ecuaciones, es posible predecir la probabilidad de cada empate dirigido en función de los parámetros del modelo. Estos se muestran como los “valores esperados P1”. Por ejemplo, el modelo predice un 93% de probabilidad de empate del actor 1 al actor 2.

El panel final de la salida muestra la diferencia entre los lazos que realmente existen, y las predicciones del modelo. El modelo predice bastante bien el empate del actor 1 al actor 2 (residual = .07), pero hace un mal trabajo al predecir la relación del actor 1 al actor 9 (residual = 0.77).

Los residuos importantes porque sugieren lugares donde otras características de la gráfica o individuos pueden ser relevantes para comprender díadas particulares, o donde los lazos entre dos actores está bien contabilizada por “demografía” básica de la red. Qué actores es probable que tengan vínculos que no son pronosticados por los parámetros del modelo también se pueden mostrar en un dendograma, como en la Figura 18.28.

Figura 18.28: Diagrama de agrupamiento P1 de la red de información Knoke

Aquí vemos que, por ejemplo, que los actores 3 y 6 tienen muchas más probabilidades de tener vínculos de lo que predice el modelo P1.