9.4: Caos en el modelo de tiempo continuo
- Page ID
- 115641
Como revisamos anteriormente, el caos es realmente fácil de mostrar en modelos de tiempo discreto. Pero el descubrimiento del caos se hizo originalmente con sistemas dinámicos de tiempo continuo, es decir, ecuaciones diferenciales. Edward Lorenz, matemático y meteorólogo estadounidense, y uno de los fundadores de la teoría del caos, encontró accidentalmente un comportamiento caótico en el siguiente modelo (llamado ecuaciones de Lorenz) que desarrolló para estudiar la dinámica de la convección atmosférica a principios de la década de 1960 [5]:
\[ \frac { d x } { d t } = s ( y - x ) \label{9.9} \]
\[\frac { d y } { d t } = r x - y - x z \label{9.10} \]
\[\frac { d z } { d t } = x y - b z \label{9.11} \]
Aquí\(s\),\(r\), y\(b\) son parámetros positivos.Se sabe que este modelo es uno de los primeros que pueden mostrar caos en tiempo continuo. Simulemos este modelo con\(s = 10\)\(r = 30\), y\(b = 3\), por ejemplo:
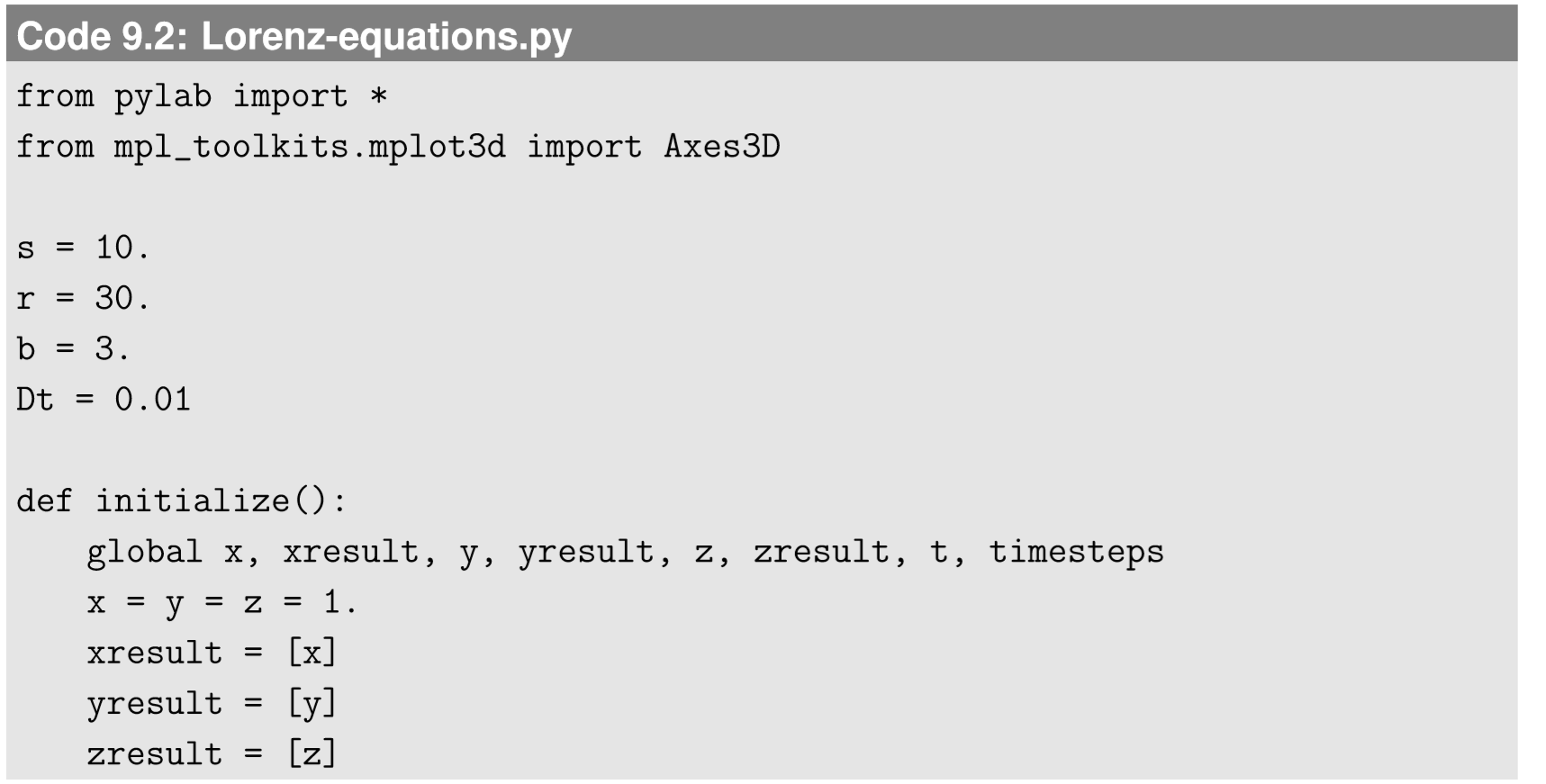




Este código produce dos salidas: una son las gráficas de series de tiempo de x, y y z (Fig. 9.4.1), y la otra es la trayectoria del estado del sistema en un espacio de fase 3-D (Fig. 9.4.2). Como puede ver en la Fig. 9.4.1, el comportamiento del sistema es altamente impredecible, pero definitivamente también hay cierta regularidad en él. x e y tienden a permanecer en el lado positivo o negativo, al tiempo que muestran algunas oscilaciones con amplitudes crecientes. Cuando la oscilación se vuelve demasiado grande, se lanzan al otro lado. Esto continúa indefinidamente, con cambios ocasionales de bando en momentos impredecibles. Mientras tanto, z permanece positivo todo el tiempo, con patrones oscilatorios similares.
Trazar estas tres variables juntas en un espacio de fase 3-D revela lo que se llama el atractor Lorenz (Fig. 9.4.2). Es probablemente el ejemplo más conocido de atractores extraños, es decir, atractores que aparecen en espacios de fase de sistemas caóticos.
Al igual que cualquier otro atractor, los atractores extraños son conjuntos de estados a los que se atraen trayectorias cercanas. Pero lo que los hace realmente “extraños” es que, aunque parezcan un objeto voluminoso, su “volumen” es cero relativo al del espacio de fase, y así tienen una dimensión fractal, es decir, una dimensión de un objeto que no es de valor entero. Por ejemplo, se sabe que la dimensión fractal del atractor Lorenz es de aproximadamente 2.06, es decir, está bastante cerca de un objeto 2-D pero no del todo. De hecho, cualquier sistema caótico tiene un atractor extraño con dimensión fractal en su espacio de fase. Por ejemplo, si miras cuidadosamente los intrincados patrones en el régimen caótico de la Fig. 8.4.3, allí también verás patrones fractales.
Dibujar trayectorias de los estados de las ecuaciones de Lorenz en un espacio de fase 3-D para varios valores diferentes de r mientras que otros parámetros se mantienen constantes. Vea cómo cambia la dinámica de las ecuaciones de Lorenz a medida que varía\(r\).
Obtener los puntos de equilibrio de las ecuaciones de Lorenz en función de\(r\), manteniendo\(s = 10\) y\(b = 3\). Luego realizar un análisis de bifurcación en cada punto de equilibrio para encontrar los umbrales críticos de r en los que se produce una bifurcación.
Compara tu resultado con los resultados de simulación numérica obtenidos en el ejercicio anterior.
Por cierto, dije antes que cualquier sistema caótico tiene dos procesos dinámicos: estirar y plegar. ¿Dónde ocurren estos procesos en el atractor Lorenz? No es tan sencillo entender completamente su estructura, pero el estiramiento ocurre donde la trayectoria está dando vueltas dentro de una de las dos “alas” del atractor. Las espirales que se ven en esas alas son inestables que van hacia afuera, por lo que la distancia entre los estados inicialmente cercanos se expande a medida que giran alrededor del foco espiral. Mientras tanto, el plegado ocurre en el centro del atractor, donde se encuentran dos “láminas” de trayectorias. Esas dos hojas en realidad nunca se cruzan entre sí, sino que se mantienen separadas entre sí, formando un “sándwich de oblea” hecho de dos capas delgadas, cuya mitad derecha pasa a circular en el ala derecha mientras que la mitad izquierda continúa hacia el ala izquierda. De esta manera, la “masa” se divide en dos, cada una de las cuales se estira, y luego las dos masas estiradas se apilan una encima de la otra para formar una nueva masa que está hecha de dos capas nuevamente. A medida que este proceso continúa, el resultado final, el atractor Lorenz, adquiere infinitamente muchas capas formadas recursivamente en él, que le dan el nombre de un atractor “extraño” con una dimensión fractal.
Trazar el atractor Lorenz en varias perspectivas diferentes (la opción más fácil sería proyectarlo en los\(x-z\) planos\(x-y\)\(y-z\),, y) y observar su estructura. Interpretar su forma y los planos de trayectorias desde un punto de vista de estiramiento y plegado.
Me gustaría sacar a colación un hecho matemático más importante antes de cerrar este capítulo:
Para que los sistemas dinámicos de tiempo continuo sean caóticos, las dimensiones del espacio de fase del sistema deben ser al menos 3-D. Por el contrario, los sistemas dinámicos de tiempo discreto pueden ser caóticos independientemente de sus dimensiones
Las ecuaciones de Lorenz involucraron tres variables, por lo que fue un ejemplo de sistemas caóticos de tiempo continuo con mínima dimensionalidad.
Este hecho se deriva del teorema de Poincar'e-Bendixson en matemáticas, que establece que ningún atractor extraño puede surgir en el espacio de fase 2-D continuo. Una explicación intuitiva de esto es que, en un espacio de fase 2-D, cada trayectoria existente funciona como un “muro” que no se puede cruzar, lo que impone limitaciones a dónde se puede ir en el futuro. En un entorno tan cada vez más restrictivo, no es posible mantener dinámicas explorando continuamente durante un período de tiempo indefinidamente largo.
Reúne un bolígrafo y un trozo de papel en blanco. Empezar a dibujar una curva continua sobre el papel que represente la trayectoria de un sistema dinámico hipotético en un espacio de fase 2-D. La forma de la curva que dibujas puede ser arbitraria, pero con las siguientes limitaciones:
• No puedes dejar que el bolígrafo se salga del papel. La curva debe ser dibujada en un trazo continuo.
• La curva no puede fundirse o cruzarse a sí misma.
• No se pueden dibujar curvas que fluyan en direcciones opuestas dentro de un área muy pequeña (esto viola la suposición de continuidad del espacio de fase).
Sigue dibujando la curva todo el tiempo que puedas, y mira qué pasa. Discutir las implicaciones del resultado para los sistemas dinámicos. Entonces considera qué pasaría si dibujaras la curva en un espacio 3-D en lugar de 2-D.
Que zi denote el valor del pico\(i\) -ésimo de\(z(t)\) producido por las ecuaciones de Lorenz. Obtener datos de series temporales\({z_1,z_2,z_3,...}\) a partir de resultados de simulación numérica. Trama\(z_t\) contra\(z_{t−1}\), como en una trama de telaraña, y mira qué tipo de estructura encuentras ahí. Haga esta visualización para diversos valores de r, manteniendo\(s = 10\) y\(b = 3\), y compare los resultados con los resultados del análisis de bifurcación obtenido en el Ejercicio 9.4.1.
Como se revisó a través de este y de capítulos anteriores, las bifurcaciones y el caos son las características más distintivas de los sistemas no lineales. Pueden producir comportamientos inesperados del sistema que a menudo son contrarios a la intuición de nuestra comprensión cotidiana de la naturaleza. Pero una vez que te das cuenta de la posibilidad de tales comportamientos del sistema y sabes cómo y cuándo pueden ocurrir, tu visión del mundo se vuelve más informada, enriquecida. Después de todo, las bifurcaciones y el caos están jugando papeles importantes en nuestros entornos físicos, biológicos, ecológicos y tecnológicos (así como dentro de nuestros cuerpos y cerebros). Por lo tanto, deben merecer nuestro aprecio.
Este capítulo concluye nuestro recorrido por sistemas con un pequeño número de variables. Cambiaremos de marcha y finalmente entraremos en el reino de los sistemas complejos que están hechos de una gran cantidad de variables en el próximo capítulo.

