9.3: Exponente de Lyapunov
- Page ID
- 115649
Por último, me gustaría introducir una métrica analítica útil que pueda ayudar a caracterizar el caos. Se llama el exponente Lyapunov, que mide la rapidez con la que crece con el tiempo una distancia infinitesimalmente pequeña entre dos estados inicialmente cercanos:
\[F^{t}(x_0 + ε)−F^{t}(x_0) ≈ εe^{λt} \label{9.2} \]
El lado izquierdo es la distancia entre dos estados inicialmente cercanos después de los\(t\) pasos, y el lado derecho es la suposición de que la distancia crece exponencialmente con el tiempo. El exponente\(λ\) medido por un largo periodo de tiempo (idealmente\(t → ∞)\) es el exponente Lyapunov. Si\(λ > 0\), pequeñas distancias crecen indefinidamente con el tiempo, lo que significa que el mecanismo de estiramiento está vigente. O si\(λ < 0\), las distancias pequeñas no crecen indefinidamente, es decir, el sistema se instala en una trayectoria periódica eventualmente. Obsérvese que el exponente de Lyapunov caracteriza sólo el estiramiento, pero como discutimos antes, el estiramiento no es el único mecanismo del caos. Hay que tener en cuenta que el mecanismo de plegado no se capta en este exponente de Lyapunov.
Podemos hacer un poco de derivación matemática para transformar la Ecuación\ ref {9.2} en una forma más fácil de calcular:
\[e^{λt} ≈ \frac{|F^{t}(x_{0} + ε)−F^{t}(x_{0})|}{ ε} \label{9.3} \]
\[\begin{align} λ &= \lim _{t→∞,ε→0} \frac{1} {t} \log{\frac{|F^{t}(x_{0} +\varepsilon)-F^{t}(x_{0})|}{\varepsilon}}\label{9.4} \\[4pt] &= \lim_{ t→∞ 1, ε→0}\frac{1} {t} \log {|\frac{dF} {dx}| _{x=x_0}|}\label{9.5} \end{align} \]
(aplicando la regla de la diferenciación en cadena...)
\[λ = \lim_{t→∞}\frac{ 1}{ t} \log {|\frac{dF}{ dx}}|_{ x=F^{t−1}(x_0)=x_{t−1}} · \frac{dF}{ dx}|_{ x=F^{t−2}(x_0)=x_{t−2}} ···· \frac{dF}{ dx}|_{x=x_{0}}\label{9.6} \]
\[ \lim_{t \rightarrow \infty }\frac{1}{t} \sum^{t-1}_{i=0} \log{|\frac{dF}{ dx}|_{ x=x_{i} }|} \label{9.7} \]
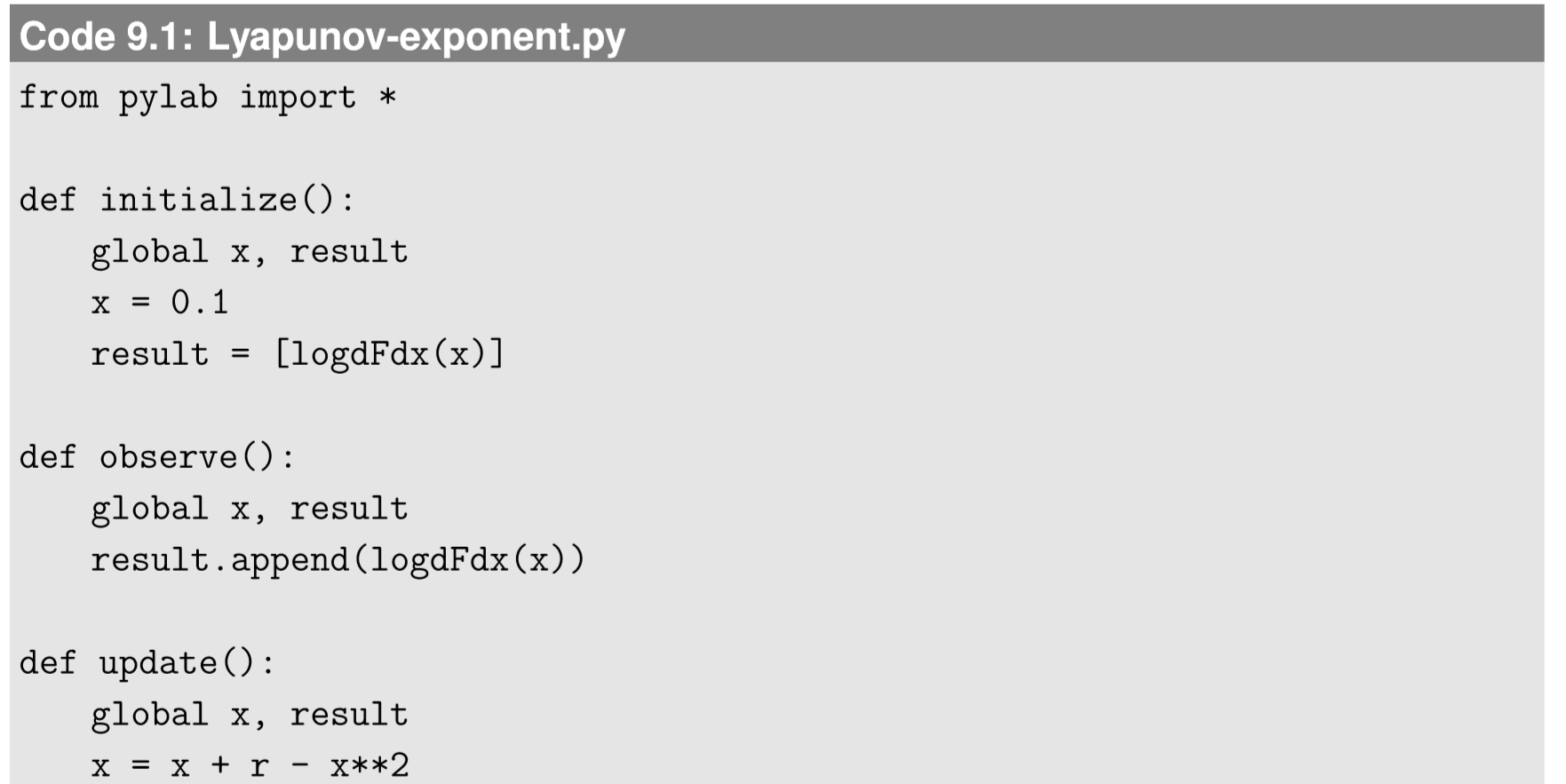
El resultado final es bastante simple: el exponente de Lyapunov es un promedio de tiempo de cada estado que visita el sistema\(log|\frac{dF}{dx}|\) a lo largo de la simulación. Esto es muy fácil de calcular numéricamente. Aquí un ejemplo de computación del exponente Lyapunov de la Eq. 8.4.3 sobre variando\(r\):



La Figura 9.3.1 muestra el resultado. Al comparar esta figura con el diagrama de bifurcación (Fig. 8.4.3), notará que el rango de parámetros donde el exponente Lyapunov toma valores positivos coincide muy bien con el rango donde el sistema muestra un comportamiento caótico. Además, siempre que se produce una bifurcación (e.g.\(r = 1\)\(1.5\),, etc.), el exponente Lyapunov toca la\(λ = 0\) línea, indicando la criticidad de esos valores de parámetros. Por último, hay varios lugares en la trama donde el exponente Lyapunov diverge hasta el infinito negativo (puede que no se vean así, pero de hecho van infinitamente profundo). Tales valores ocurren cuando el sistema converge a un punto de equilibrio extremadamente estable con\(\frac{dF^{t}}{dx}_{|x=x_{0}} ≈ 0\) por cierto\(t\). Dado que la definición del exponente Lyapunov contiene logaritmos de esta derivada, si se convierte en cero, el exponente diverge también al infinito negativo.
Trazar el exponente Lyapunov del mapa logístico (Eq. (\ ref {8.4.9}) para\(0 < r < 4\), y compara el resultado con su diagrama de bifurcación.
Trazar el diagrama de bifurcación y el exponente Lyapunov del siguiente sistema dinámico de tiempo discreto para\(r > 0\):
\[x_{t}= cos^{2}(rx_{t-1})\label{9.8} \]
Luego explique con palabras cómo cambia su dinámica\(r\).

