13.1: Modelos de Campo Continuo con Ecuaciones Diferenciales Parciales

La dinámica espacio-temporal de sistemas complejos también se puede modelar y analizar mediante ecuaciones diferenciales parciales (PDE), es decir, ecuaciones diferenciales cuyas variables independientes incluyen no solo el tiempo, sino también el espacio. Como marco de modelado, las PDEs son mucho más antiguas que CA. Pero curiosamente, las aplicaciones de las PDEs para describir dinámicas autoorganizativas de sistemas extendidos espacialmente comenzaron aproximadamente al mismo tiempo que los estudios de CA. Como se discutió en la Sección 11.5, el trabajo monumental de Turing sobre la base química de la morfogénesis [44] jugó un papel importante en el encendido de la atención de los investigadores hacia los modelos de campo continuos basados en PDE como marco matemático para estudiar la autoorganización de sistemas complejos.

Hay muchas formas diferentes de formular un modelo basado en PDE, pero aquí nos atenemos a la siguiente formulación matemática simple de primer orden:

\[\frac{\partial{f}}{\partial{t}}=F(f, \frac{\partial{f}}{\partial{x}}, \frac{\partial^{2}f}{\partial{x^{2}}}, ....,x, t) \label{(13.1)} \]

Ahora las derivadas parciales (e.g.,\(∂f/∂t\)) han comenzado a aparecer en las ecuaciones, pero no tengas miedo; no son nada diferentes de las derivadas ordinarias (e.g.,\(df/dt\)). Derivadas parciales simplemente significan que la función que se está diferenciando tiene más de una variable independiente (e.g.\(x\),\(t\)) y que la diferenciación se está haciendo mientras que otras variables independientes se mantienen como constantes. La fórmula anterior sigue siendo sobre el cambio instantáneo de algo a lo largo del tiempo (como se ve en el lado izquierdo), lo que es consistente con lo que hemos hecho hasta ahora, por lo que encontrará esta formulación relativamente fácil de entender y simular.

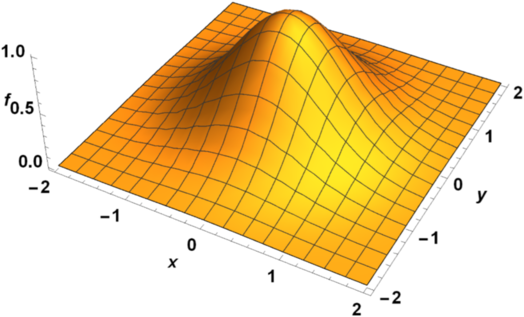
Tenga en cuenta que la variable ya no\(x\) es una variable de estado del sistema, sino que representa una posición en un espacio continuo. Mientras tanto, el estado del sistema ahora está representado por una función, o un campo\(f(x,t)\), que se define sobre un espacio continuo así como a lo largo del tiempo (por ejemplo, Fig. 13.1). El valor de la función\(f\) podría ser escalar o vectorial. Ejemplos de tales campos continuos incluyen densidad de población (campo escalar) y flujos de corrientes oceánicas (campo vectorial).

Figura\(\PageIndex{1}\): Ejemplo de una función espacial (campo) definida sobre un espacio bidimensional. La función\(f(x,y) = e^{-(x^2+y^2)}\) se muestra aquí.

En la Ecuación\ ref {(13.1)}, el lado derecho aún puede contener espacio\(x\) y tiempo\(t\)), lo que significa que esta puede ser una ecuación no autónoma. Pero como ya sabemos, las ecuaciones no autónomas pueden convertirse en ecuaciones autónomas usando el truco que se discute en la Sección 6.2. Por lo tanto, nos centraremos en los modelos autónomos en este capítulo.

Como puede ver en el lado derecho de la Ecuación\ ref {(13.1)}, el modelo ahora puede incluir derivadas espaciales del campo, lo que da información sobre cómo se forma espacialmente el estado del sistema. La interacción entre las derivadas espaciales (forma, estructura) y las derivadas temporales (comportamiento, dinámica) hace que los modelos de campo continuos sean particularmente interesantes y útiles.

En cierto sentido, usar una función continua como estado del sistema significa que el número de variables (es decir, los grados de libertad) en el sistema es ahora infinito. Debes estar orgulloso de ver este hito; hemos recorrido un largo camino para llegar a este punto, partiendo de una sola ecuación dinámica variable, pasando por CA con miles de variables, ¡hasta finalmente enfrentar sistemas con infinitamente muchas variables!

Pero claro, en realidad no somos capaces de modelar o analizar sistemas hechos de infinitamente muchas variables. Con el fin de reducir estos modelos matemáticos por lo demás infinitamente complejos a algo manejable para nosotros que tenemos inteligencia finita y vida útil, generalmente asumimos la suavidad de la función\(f\). Es por ello que podemos describir la forma y el comportamiento de la función utilizando derivados bien definidos, lo que aún puede permitirnos estudiar sus propiedades utilizando medios analíticos ¹.

¹ Pero también debemos tener en cuenta que no todos los sistemas físicamente importantes e interesantes pueden ser representados por funciones espaciales suaves. Por ejemplo, los campos electromagnéticos y gravitacionales pueden tener singularidades donde se rompe la suavidad y los valores de estado y/o sus derivados divergen hasta el infinito. Si bien tales singularidades juegan un papel importante en la naturaleza, aquí nos limitamos solo a funciones espaciales continuas y suaves.