13.2: Fundamentos del Cálculo Vectorial
- Page ID
- 115877
Para desarrollar modelos de campo continuos, es necesario conocer algunos conceptos matemáticos básicos desarrollados y utilizados en el cálculo vectorial. A continuación se da una revisión rápida minimalista de esos conceptos.
Un contorno es un conjunto de posiciones espaciales\(x\) que satisfacen
\[f(x) = C\label{(13.2)} \]
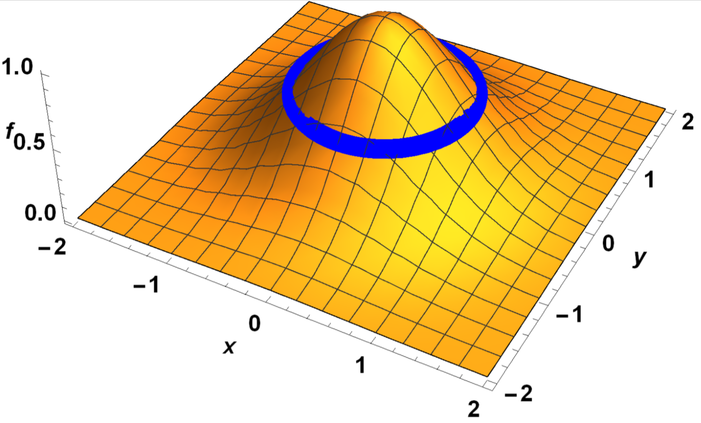
para un campo escalar\(f\), donde\(C\) es una constante (ver un ejemplo en la Figura\(\PageIndex{1}\)). Los contornos también se denominan curvas de nivel o superficies.
Un gradiente de un campo escalar\(f\) es un vector definido localmente como
\[∇f = \begin{pmatrix} \dfrac{\partial{f}}{\partial{x_{1}}} \\ \dfrac{\partial{f}}{\partial{x_{2}}} \\ \vdots \\ \dfrac{\partial{f}}{\partial{x_{n}}} \end{pmatrix} \label{(13.3)} \]
Aquí,\(n\) está el número de dimensiones del espacio.
El símbolo\(∇\) se llama “del” o “nabla”, que puede considerarse el siguiente “vector” de operadores diferenciales:
\[\nabla =\begin{pmatrix} \dfrac{\partial}{\partial{x_{1}}} \\\dfrac{\partial}{\partial{x_{2}}}\\ \vdots \\ \dfrac{\partial}{\partial{x_{n}}} \end{pmatrix}\label{(13.4)} \]
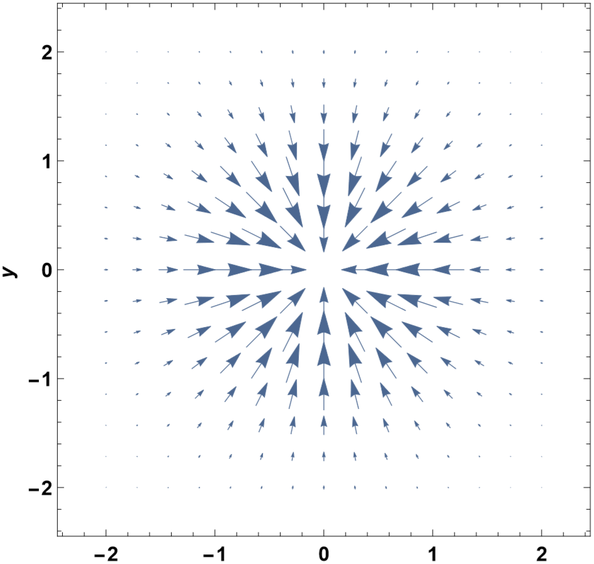
Un gradiente de\(f\) en posición\(x\) es un vector que apunta hacia la dirección de la pendiente ascendente más pronunciada de\(f\) at\(x\). La longitud del vector representa cuán empinada es la pendiente. Un campo vectorial de gradiente\(∇f\) definido sobre un campo escalar a menudo\(f\) se denomina campo de gradiente (Vea un ejemplo en la Figura\(\PageIndex{2}\)). El gradiente siempre es perpendicular al contorno que atraviesa\(x\) (a menos que el gradiente sea un vector cero; compárese las Figs. 13.2.1 y 13.2.2).
Una divergencia de un campo vectorial\(v\) es un campo escalar definido como
\[\nabla \cdot v = \left( \begin{array} { c } { \frac { \partial } { \partial x _ { 1 } } } \\ { \frac { \partial ^ { 1 } } { \partial x _ { 2 } } } \\ { \frac { \vdots } { \partial x _ { n } } } \end{array} \right) ^ { T } \left( \begin{array} { c } { v _ { 1 } } \\ { v _ { 2 } } \\ { \vdots } \\ { v _ { n } } \end{array} \right) = \frac { \partial v _ { 1 } } { \partial x _ { 1 } } + \frac { \partial v _ { 2 } } { \partial x _ { 2 } } + \ldots + \frac { \partial v _ { n } } { \partial x _ { n } }. \label{(13.5)} \]
Tenga en cuenta el pequeño punto entre\(∇\) y\(v\), lo que indica que este es un “producto interno” de ellos. ¡No confundas esta divergencia con el gradiente discutido anteriormente!
El significado físico de la divergencia no es tan sencillo de entender, pero de todos modos, literalmente cuantifica cuánto “diverge” el campo\(v\) vectorial de la ubicación\(x\). Pasemos por un ejemplo para un espacio 2-D. Supongamos\(v\) que representa flows de algunas “cosas” moviéndose en un espacio 2-D. El material está hecho de un gran número de partículas (como un gas hecho de moléculas), y el flujo\(v = (v_x,v_y)\) significa cuántas partículas están atravesando una sección transversal del espacio por área por unidad de tiempo. En este ejemplo 2-D, una sección transversal significa un segmento de línea en el espacio, y el área total de la sección es solo la longitud del segmento de línea.
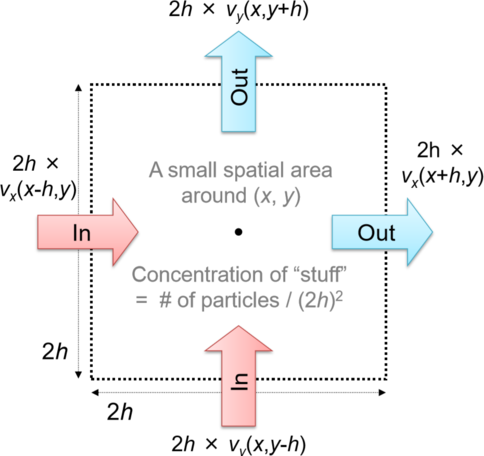
Entonces, consideremos un cambio temporal del número de partículas, digamos\(N\), dentro de un área espacial muy pequeña alrededor de (\(x\),\(y\)) Figura\(\PageIndex{3}\). El cambio temporal de se\(N\) puede calcular contando cuántas partículas entran o salen del área a través de cada borde por unidad de tiempo, como
\[\frac{\partial{N}}{\partial{t}} =2hv_{x}(x-h,y) +2hv_{y}(x, y-h) -2hv_{x} (x+h,y) -2hv_{y}(x, y+h), \label{(13.6)} \]
donde\(h\) es la distancia de (\(x\),\(y\)) a cada borde, y por lo tanto la longitud de cada borde es\(2h\).
En realidad, la Figura\(\PageIndex{3}\) puede ser un poco engañosa; las partículas pueden entrar y salir por cualquier borde en ambas direcciones. Pero usamos el\(+\) letrero para\(v_{x}(x−h,y)\) y\(v_{y}(x,y−h)\) y el\(−\) signo para\(v_{x}(x + h,y)\) y\(v_{y}(x,y + h)\) en la Eq. (\ ref {(13.6)}), porque las velocidades se miden utilizando el sistema de coordenadas donde las direcciones hacia la derecha y hacia arriba se consideran positivas.
Ya que\(N\) depende del tamaño del área, podemos dividirla por el área (\((2h)^{2}\)en este caso) para calcular el cambio en términos de la concentración de las partículas,\(c = N/(2h)^{2}\), lo que no dependerá de\(h\):
\[ \begin{align} \frac{\partial{c}}{\partial{t}} &= \frac{2hv_{x}(x-h, y) + 2hv_{y}(x, y-h) -2hv_{x}(x+h, y) -2hv_{y}(x, y+h)}{(2h)^{2}} \label{(13.7)} \\[4pt] &=\frac{v_{x} (x-h,y) +v_{y} (x, y-h) -v_{x}(x+h, y) -v_{y}(x, y+h)}{2h} \label{(13.8)} \end{align} \]
Si hacemos que el tamaño del área sea realmente pequeño\((h → 0)\), esto se convierte en el siguiente:
\[ \begin{align} \frac{\partial{c}}{\partial{t}} &=\lim_{h \rightarrow{0}} \frac{v_{x}(x-h, y) +v_{y}(x, y-h) -v_{x}(x+h, y) -v_{x}(x+h, y) -v_{y}(x, y+h)}{2h}\label{(13.9)} \\[4pt] &=\lim_{h\rightarrow{0}} \begin{Bmatrix}(-\frac{ v_{x}(x+h, y)-v_{x}(x-h, y)}{2h}) +(-\frac{v_{y} (x, y+h) -v_{y} (x, y -h)}{2h}) \end{Bmatrix} \label{(13.10)} \\[4pt] &= -\frac{\partial{v_{x}}}{\partial{x}} -\frac{\partial{v_{y}}}{\partial{y}} \label{(13.11)} \\[4pt] &=−∇ \cdot{v}\label{(13.12)} \end{align} \]
En palabras naturales, esto significa que el cambio temporal de una concentración de las cosas viene dado por una divergencia negativa del campo vectorial\(v\) que describe su movimiento. Si la divergencia es positiva, eso significa que las cosas se están escapando del área local. Si la divergencia es negativa, las cosas están fluyendo hacia el área local. La derivación matemática anterior confirma esta comprensión intuitiva de la divergencia
Confirmar que la interpretación de divergencia anterior también se aplica a los casos 3-D.
Un Laplaciano de un campo escalar\(f\) es un campo escalar definido como
\[∇^{2}f =∇ \cdot{∇f} ={\begin{pmatrix} \frac{\partial}{\partial{x_{1}}} \\ \frac{\partial}{\partial{x_{2}}} \\ \vdots \\ \frac{\partial}{\partial{x_{n}}} \end{pmatrix}}^{T} \begin{pmatrix} \frac{\partial}{\partial{x_{1}}} \\ \frac{\partial}{\partial{x_{2}}} \\ \vdots \\ \frac{\partial}{\partial{x_{n}}} \end{pmatrix} f = \frac{\partial^{2}{f}} {\partial{x^{2}_{1}}} +\frac{\partial^{2}{f}}{\partial{x^{2}_{2}}} +...+ \frac{\partial^{2}{f}} {\partial{x^{2}_{n}}}. \label{(13.13)} \]
En ocasiones el operador laplaciano se denota con un triángulo derecho hacia arriba\(∆\) en lugar de\(∇^2\). Esto es tan confuso, lo sé, pero culpar a la gente que inventó esta notación. En este libro de texto, usamos en\(∇^2\) lugar de denotar\(∆\) a los laplacianos, porque\(∇^2\) es más intuitivo para mostrar que es un operador diferencial de segundo orden, y también porque ya\(∆\) se usa para representar pequeñas cantidades (e.g.,\(∆x\)).
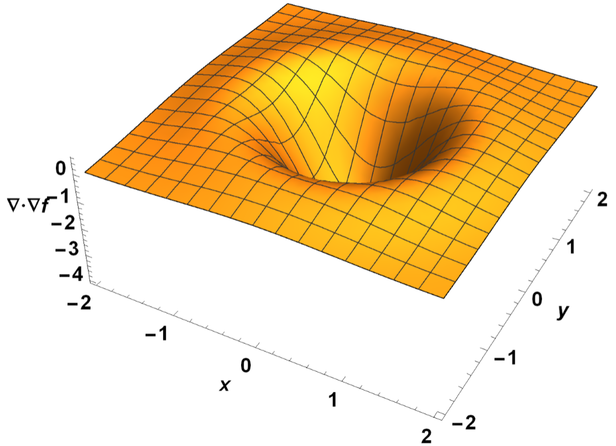
El campo de gradiente de\(f\) muestra un patrón divergente donde el campo escalar\(f\) es cóncavo como una inmersión o un valle, o un patrón convergente donde\(f\) es convexo como una joroba o una cresta. Por lo tanto, el Laplaciano de\(f\), que es la divergencia del campo de gradiente de\(f\), tiene un valor positivo donde\(f\) es cóncavo, o un valor negativo donde\(f\) es convexo. Esto es similar a la derivada de segundo orden de una función matemática; una función cóncava tiene una derivada positiva de segundo orden mientras que una función convexa tiene una negativa. El Laplaciano es una generalización del mismo concepto, aplicable a funciones definidas sobre un dominio multidimensional.
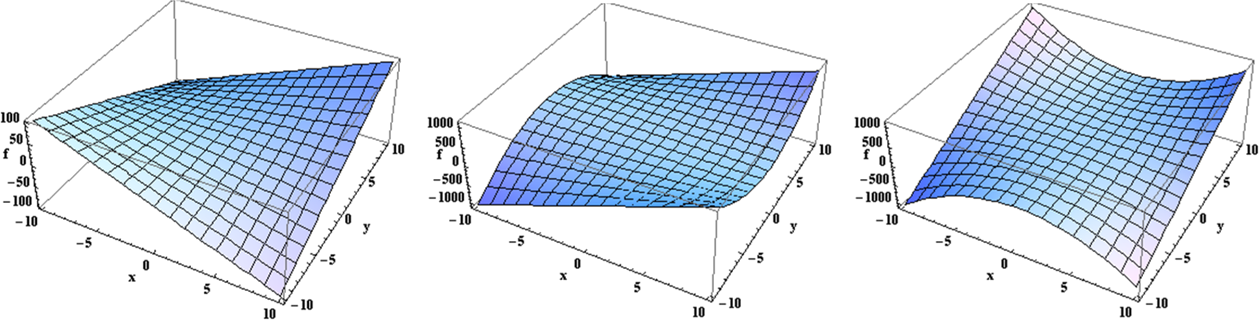
¿Cuál de las siguientes gráficas de superficie ilustra correctamente la forma de un campo escalar\(f(x,y) = xy(x−1)\)?
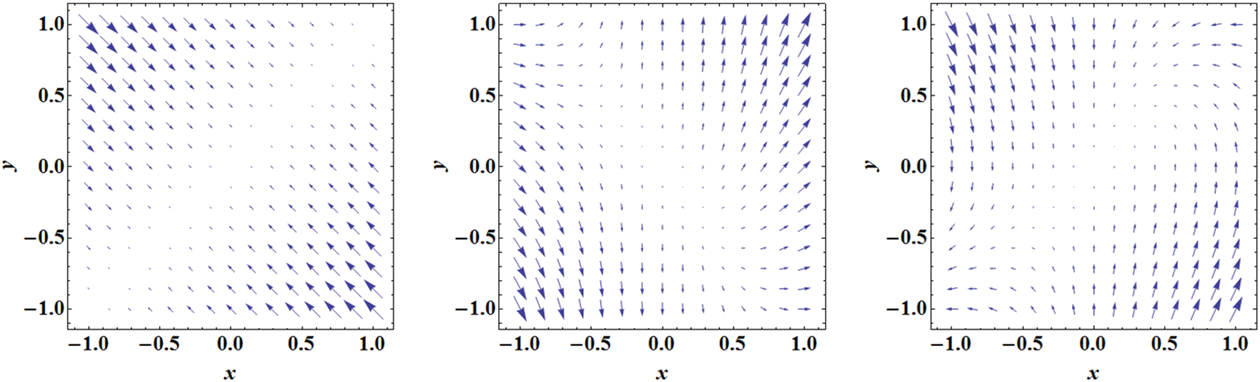
¿Cuál de las siguientes gráficas de campo vectorial ilustra correctamente los campos dados por un campo vectorial\(v(x,y) = (−xy,x−y)\)?
Calcular el campo degradado y el Laplaciano de cada uno de los siguientes:
- \(f(x, y) =x^{2} +xy\)
- \(f(x,y) =e^{x+y}\)
- \(f(x, y, z) =\frac{x+y}{z}\)
Explique dónde en el\(x-y\) espacio la superficie definida por\(f(x,y) = 3x^{2} −xy^{3}\) los interruptores entre cóncava y convexa.
Hasta ahora, el gradiente se define solo para un campo escalar, pero también es natural definir un gradiente para un campo vectorial. Proponer una definición significativa\(∇v\) y discutir su significado físico.

