13.6: Sistemas de Reacción-Difusión
- Page ID
- 115868
Por último, me gustaría introducir sistemas de reacción-difusión, una clase particular de modelos de campo continuo que han sido ampliamente estudiados. Son modelos de campo continuo cuyas ecuaciones están hechas únicamente de términos de reacción y términos de difusión, como se muestra a continuación:
\[\dfrac{\partial{f_1}}{\partial{t}} =R_1(f_1,f_2,...,f_n) + D_1∇^{2}f_1 \label{(13.53)} \]
\[\dfrac{\partial{f_2}}{\partial{t}} = R_2 (f_1,f_2,...,f_n) + D_2∇^{2}f_2 \label{(13.54)} \]
\[ \vdots \nonumber \]
\[\dfrac{\partial{f_n}}{\partial{t}} =R_n(f_1,f_2,...,f_n) + D_n∇^{2}f_n \label{(13.55)} \]
Los términos de reacción (\(R_i(...)\)) describen solo dinámicas locales, sin ninguna derivada espacial involucrada. Los términos de difusión (\(D_i∇^{2}f_i\)) están estrictamente limitados a la propia variable laplaciana de estado. Por lo tanto, cualquier ecuación que implique movimiento espacial no difusivo (por ejemplo, quimiotaxis) no son sistemas de reacción-difusión.
Hay varias razones por las que los sistemas de reacción-difusión han sido una opción popular entre los modeladores matemáticos de fenómenos espacio-temporales. En primer lugar, su clara separación entre dinámicas no espaciales y espaciales hace que las tareas de modelado y simulación sean realmente fáciles. Segundo, limitar el movimiento espacial a solo difusión hace que sea bastante sencillo expandir cualquier modelo dinámico no espacial existente en otros distribuidos espacialmente. En tercer lugar, la estructura particular de las ecuaciones de reacción-difusión proporciona un atajo fácil en el análisis de estabilidad (que se discutirá en el siguiente capítulo). Y finalmente, a pesar de la simplicidad de su forma matemática, los sistemas de reacción-difusión pueden mostrar dinámicas espacio-temporales sorprendentemente ricas y complejas. Debido a estas propiedades, los sistemas de difusión de reacción se han utilizado ampliamente para modelar la autoorganización de patrones espaciales. Incluso hay aplicaciones de software especializadas disponibles exactamente para simular sistemas de reacción-difusión 3.
Extender los siguientes modelos no espaciales en otros distribuidos espacialmente como sistemas de reacción-difusión mediante la adición de términos de difusión. Después simula sus comportamientos en Python.
- Movimiento de un péndulo (Eq. (6.2 .1)): Esto crea un modelo espacial de osciladores no lineales acoplados localmente.
- Modelo Susceptible-Infectado-Recuperado (SIR) (Ejercicio 7.1.3): Esto crea un modelo espacial de dinámica epidemiológica.
En lo que sigue, revisaremos algunos sistemas conocidos de reacción-difusión para echar un vistazo al rico y diverso mundo de sus dinámicas.
Formación de patrón de Turing
Como se mencionó al principio de este capítulo, los modelos PDE de Alan Turing se encontraban entre los primeros sistemas de reacción-difusión desarrollados a principios de la década de 1950 [44]. Una versión lineal simple de las ecuaciones de Turing es la siguiente:
\[\dfrac{\partial{u}}{\partial{t}} =a(u-h) +b(v-k) +D_{u}\Delta^{2}u \label{13.56} \]
\[\dfrac{\partial{u}}{\partial{t}} =c(u-h) +d(v-k) +D_{u}\Delta^{2}u \label{13.57} \]
Las variables de estado\(u\) y\(v\) representan concentraciones de dos especies químicas. \(a, b, c,\)y\(d\) son parámetros que determinan el comportamiento de los términos de reacción, mientras\(h\) y\(k\) son constantes. Finalmente,\(D_u\) y\(D_v\) son constantes de difusión.
Si se ignoran los términos de difusión, es fácil demostrar que este sistema tiene sólo un punto de equilibrio, (\(u_eq,v_eq) = (h,k)\). Este punto de equilibrio puede ser estable para muchos valores de parámetros para\(a, b, c,\) y\(d\). Lo más sorprendente de los hallazgos de Turing es que, incluso para puntos de equilibrio tan estables, introducir dimensiones espaciales y términos de difusión en las ecuaciones puede desestabilizar el equilibrio, y así el sistema puede autoorganizarse espontáneamente en un patrón no homogéneo. Esto se llama inestabilidad inducida por difusión o inestabilidad de Turing. Un resultado de simulación de muestra se muestra en la Fig. 13.6.1.
La idea de inestabilidad inducida por difusión es bastante contraintuitiva. La difusión suele considerarse una fuerza aleatoria que destruye cualquier estructura en un lío homogeneizado, sin embargo, en este modelo en particular, ¡la difusión es la clave para la autoorganización! ¿Qué está pasando? El truco es que este sistema tiene dos coeficientes de difusión diferentes,\(D_u\) y\(D_v\), y su diferencia juega un papel clave en la determinación de la estabilidad del estado del sistema. Esto se discutirá con más detalle en el próximo capítulo.
Hay una cosa que necesita especial atención cuando estás a punto de simular las ecuaciones de reacción-difusión de Turing. La formación del patrón Turing requiere pequeñas perturbaciones aleatorias (ruido) para estar presentes en la configuración inicial del sistema; de lo contrario, no habría manera de que la dinámica rompa la simetría espacial para crear patrones no homogéneos. Mientras tanto, tales perturbaciones iniciales deberían ser lo suficientemente pequeñas para que no causen inmediatamente inestabilidades numéricas en la simulación. Aquí hay un código de muestra para simular la formación de patrones de Turing con un nivel sugerido de perturbaciones iniciales, usando los ajustes de parámetros mostrados en la Fig. 13.6.1:
Esta simulación parte de una configuración inicial\((u(x,y),v(x,y)) ≈ (1,1) = (h,k)\), que es el estado de equilibrio homogéneo del sistema que sería estable sin términos de difusión. ¡Ejecuta la simulación para ver cómo los patrones se autoorganizan espontáneamente!
Realizar simulaciones de la formación del patrón de Turing con varios parámetros diferentes, y discutir cómo las variaciones de parámetros (especialmente para las constantes de difusión) afectan la dinámica resultante.
Discretizar el modelo de agregación de moldes de limo Keller-Segel (Eqs. (13.4.13) y (13.4.14)) (aunque este modelo no es un sistema de reacción-difusión, este es el momento perfecto para que trabajes en este ejercicio porque puedes utilizar el Código 13.8). Implementar su código de simulación en Python, y realizar simulaciones con\(µ = 10^{−4}\),\(D = 10^{−4}\),\(f = 1\), y\(k = 1\), mientras varía\(χ\) como un parámetro de control que va desde\(0\) hasta\(10^{−3}\). Uso\(a = 1\) y\(c = 0\) como condiciones iniciales en todas partes, con pequeñas perturbaciones aleatorias agregadas a ellas.
Reacción Belousov-Zhabotinsky
La reacción Belousov-Zhabotinsky, o reacción BZ para abreviar, es una familia de reacciones químicas oscilatorias descubiertas por primera vez por el químico ruso Boris Belousov en la década de 1950 y luego analizadas por el químico ruso-estadounidense Anatol Zhabotinsky en la década de 1960. Una de las variaciones comunes de esta reacción es esencialmente una oxidación del ácido malónico (\(CH_{2}(COOH)_{2}\)) por una solución de bromato acidificada, sin embargo, este proceso muestra un comportamiento oscilatorio no lineal o un período de tiempo sustancial antes de alcanzar finalmente el equilibrio químico. El mecanismo químico real es bastante complejo, involucrando alrededor de 30 sustancias químicas diferentes. Además, si esta solución química se coloca en una placa de Petri poco profunda, la oscilación química comienza en diferentes fases en diferentes ubicaciones. La interacción entre la reacción y la difusión de los químicos sobre el espacio dará como resultado la autoorganización de ondas dinámicas viajeras (Figura\(\PageIndex{2}\)), al igual que las que se ven en el modelo CA de medios excitables en la Sección 11.5.
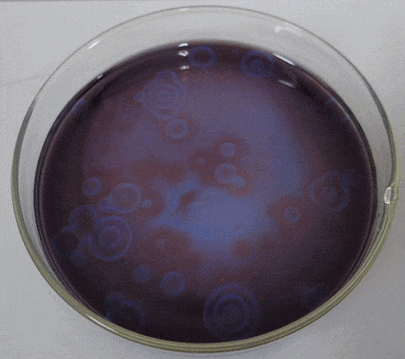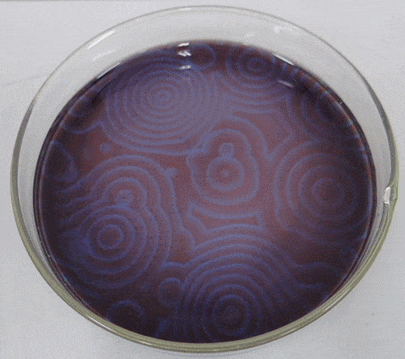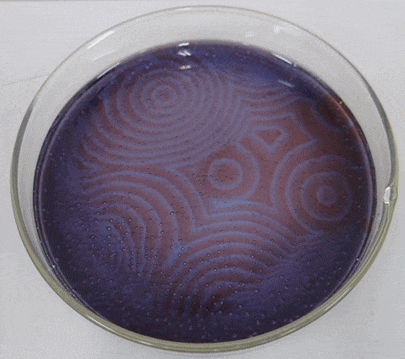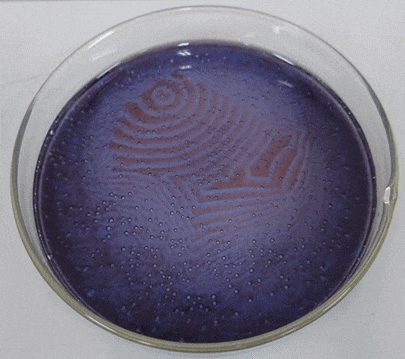
Un modelo matemático simplificado llamado “Orégonador” fue uno de los primeros en describir la dinámica de la reacción BZ en una forma simple [50]. Originalmente se propuso como un modelo no espacial con tres variables de estado, pero posteriormente el modelo se simplificó para tener solo dos variables y luego se extendió a dominios espaciales [51]. Aquí están las ecuaciones simplificadas de “Oregonator”:
\[ \begin{align} \epsilon{\dfrac{\partial{u}}{\partial{t}}} &= u(1-u)-\dfrac{u-q}{u+q}fv + D_{u}\Delta^{2}u \label{(13.58)} \\[4pt] \dfrac{∂v}{∂t} &=u-v + D_{u}\Delta^{2}v \label{(13.59)} \end{align} \]
Aquí,\(u\) y\(v\) representan las concentraciones de dos especies químicas. Si examina cuidadosamente los términos de reacción de estas ecuaciones, notará que la presencia de químicos\(u\) tiene un efecto positivo en ambos\(u\) y\(v\), mientras que la presencia de químicos\(v\) tiene un efecto negativo en ambos. Por lo tanto, a estos químicos se les llama el “activador” y el “inhibidor”, respectivamente. Interacciones similares entre el activador y el inhibidor también se observaron en la formación del patrón de Turing, pero el sistema de reacción BZ muestra oscilación química no lineal. Esto provoca la formación de olas viajeras. A veces esas ondas pueden formar espirales si la simetría espacial se rompe por factores estocásticos. Un resultado de simulación de muestra se muestra en la Fig. 13.6.3.
Implementar un código de simulador del modelo “Oregonator” de la reacción BZ en Python. Luego realice simulaciones con varios ajustes de parámetros diferentes, y discuta qué tipo de condiciones serían necesarias para producir ondas viajeras.
Formación de Patrón de Gris-Scott
El último ejemplo es el modelo de Gray-Scott, otro sistema de reacción-difusión muy conocido estudiado y popularizado por John Pearson en la década de 1990 [52], basado en un modelo de reacción química desarrollado por Peter Gray y Steve Scott en la década de 1980 [53, 54, 55]. Las ecuaciones del modelo son las siguientes:
\[ \dfrac{∂u}{∂t} =F(1-u) -uv^{2} +D_{u}\Delta^{2}u \label{(13.60)} \]
\[\dfrac{∂v}{∂t} =-(F+k)v +uv^{2}+ D_{u}\Delta^{2}v \label{(13.61)} \]
Los términos de reacción de este modelo suponen la siguiente reacción autocatalítica (es decir, reacción química para la que el reactivo en sí sirve como catalizador):
\[u+2v \rightarrow 3v \label{(13.62)} \]
Esta reacción toma una molécula de\(u\) y la convierte en una molécula de\(v\), con ayuda de otras dos moléculas de\(v\) (de ahí, autocatálisis). Esto se representa por el segundo término en cada ecuación. Mientras tanto,\(u\) se repone continuamente desde la fuente externa hasta 1 (el primer término de la primera ecuación) a velocidad de alimentación\(F\), mientras que\(v\) se elimina continuamente del sistema a una velocidad ligeramente más rápida que\(u\) la de reposición (\(F +k \)visto en el primer término del segunda ecuación). \(F\)y\(k\) son los parámetros clave de este modelo.
Es fácil demostrar que, si se ignoran los términos de difusión, este sistema siempre tiene un punto de equilibrio en\((u_{eq},v_{eq}) = (1,0)\) (que es estable para cualquier positivo\(F\) y\(k\)). Sorprendentemente, sin embargo, este modelo puede mostrar dinámicas muy exóticas, de aspecto biológico si ciertos patrones espaciales se colocan en el equilibrio anterior. Sus comportamientos son asombrosamente ricos, incluso incluyendo crecimiento, división y muerte de “células” si se eligen apropiadamente los valores de los parámetros y las condiciones iniciales. ¡Vea la Fig. 13.6.4 para ver solo algunas muestras de su asombrosa dinámica!
Implementar un código de simulador del modelo Gray-Scott en Python. Luego realice simulaciones con varios ajustes de parámetros diferentes y discuta cómo afectan los parámetros a los patrones resultantes.
Figura\(\PageIndex{4}\): (Página siguiente) Muestras de patrones generados por el modelo de Gray-Scott con\(D_u = 2 × 10^{−5}\) y\(D_v = 10^{−5}\). La concentración de químicos\(u\) se grafica en escala de grises (más brillante = mayor, solo en esta figura). El tiempo fluye de izquierda a derecha. Los valores de los parámetros de\(F\) y\(k\) se muestran encima de cada resultado de simulación. Las condiciones iniciales son el equilibrio homogéneo en\((u,v) = (1,0)\) todas partes del espacio, excepto en el centro donde el estado local se invierte de tal manera que\((u,v) = (0,1)\).
3 Por ejemplo, echa un vistazo a Ready (https://code.google.com/p/reaction-diffusion/).

