14.1: Encontrar estados de equilibrio
- Page ID
- 115910
Una cosa buena de los modelos de campo continuo basados en PDE es que, a diferencia de los modelos de CA, todo sigue escrito en ecuaciones diferenciales suaves por lo que es posible que podamos realizar análisis matemáticos sistemáticos para investigar su dinámica (especialmente su estabilidad o inestabilidad) utilizando las mismas técnicas que esas aprendimos para sistemas dinámicos no espaciales en el Capítulo 7.
El primer paso es, como siempre, encontrar los estados de equilibrio del sistema. Tenga en cuenta que esto ya no se trata de “puntos” de equilibrio, porque el estado del sistema ahora tiene extensiones espaciales. En este caso, el estado de equilibrio de un modelo autónomo de campo continuo
\[ \frac{\partial{f}}{\partial{t}} =F(f, \frac{\partial{f}}{\partial{x}}, \frac{\partial^{2}{f}}{\partial{x^2}} \dots) \label{(14.1)} \]
se da como una función espacial estática\(f_{eq}(x)\), que satisface
\[0=F(f_{eq}, \frac{\partial{f_{eq}}}{\partial{x}}, \frac{\partial^{2}{f}}{\partial{x^2}} \dots). \label{(14.2)} \]
Un modelo simple de fuente/sumidero sinusoidal
Por ejemplo, obtengamos el estado de equilibrio de una ecuación de difusión en un espacio 1-D con un simple término de fuente/sumidero sinusoidal:
\[\frac{\partial{c}}{\partial{t}} =D\nabla^{2}c +\sin{x} \qquad (-\pi \leq {x} \leq {\pi}) \label{(14.3)} \]
El término fuente/sumidero\(\sin{x}\) significa que la “materia” se está produciendo donde\(0 < x ≤ π\), mientras se está drenando donde\(−π ≤ x < 0\). Matemáticamente hablando, este sigue siendo un sistema no autónomo porque la variable independiente\(x\) aparece explícitamente en el lado derecho. Pero esta no autonomía se puede eliminar fácilmente\(x\) reemplazando por una nueva variable de estado\(y\) que satisfaga
\[\frac{\partial{y}}{\partial{t}} =0, \label{(14.4)} \]
\[ y(x, 0) =x. \label{(14.5)} \]
En lo siguiente, seguiremos utilizando\(x\) en lugar de\(y\), solo para que la discusión sea más fácil e intuitiva.
Para encontrar un estado de equilibrio de este sistema, necesitamos resolver lo siguiente:
\[0= D\nabla^{2}c_{eq} +\sin{x} \label{(14.6)} \]
\[=D\frac{d^{2}c_{eq}}{dx^{2}} +\sin{x} \label{(14.7)} \]
Se trata de una simple ecuación diferencial ordinaria, porque no hay tiempo ni dimensiones espaciales adicionales en ella. Puedes resolverlo fácilmente a mano para obtener la solución
\[c_{eq}(x) =\frac{\sin{x}}{D} +C_{1}{x}+C_{2} \label{(14.8)} \]
donde\(C_1\) y\(C_2\) son las constantes de integración. Cualquier estado que satisfaga esta fórmula permanece sin cambios a lo largo del tiempo. La figura\(\PageIndex{1}\) muestra tal ejemplo con\(D = C_1 = C_2 = 1\).
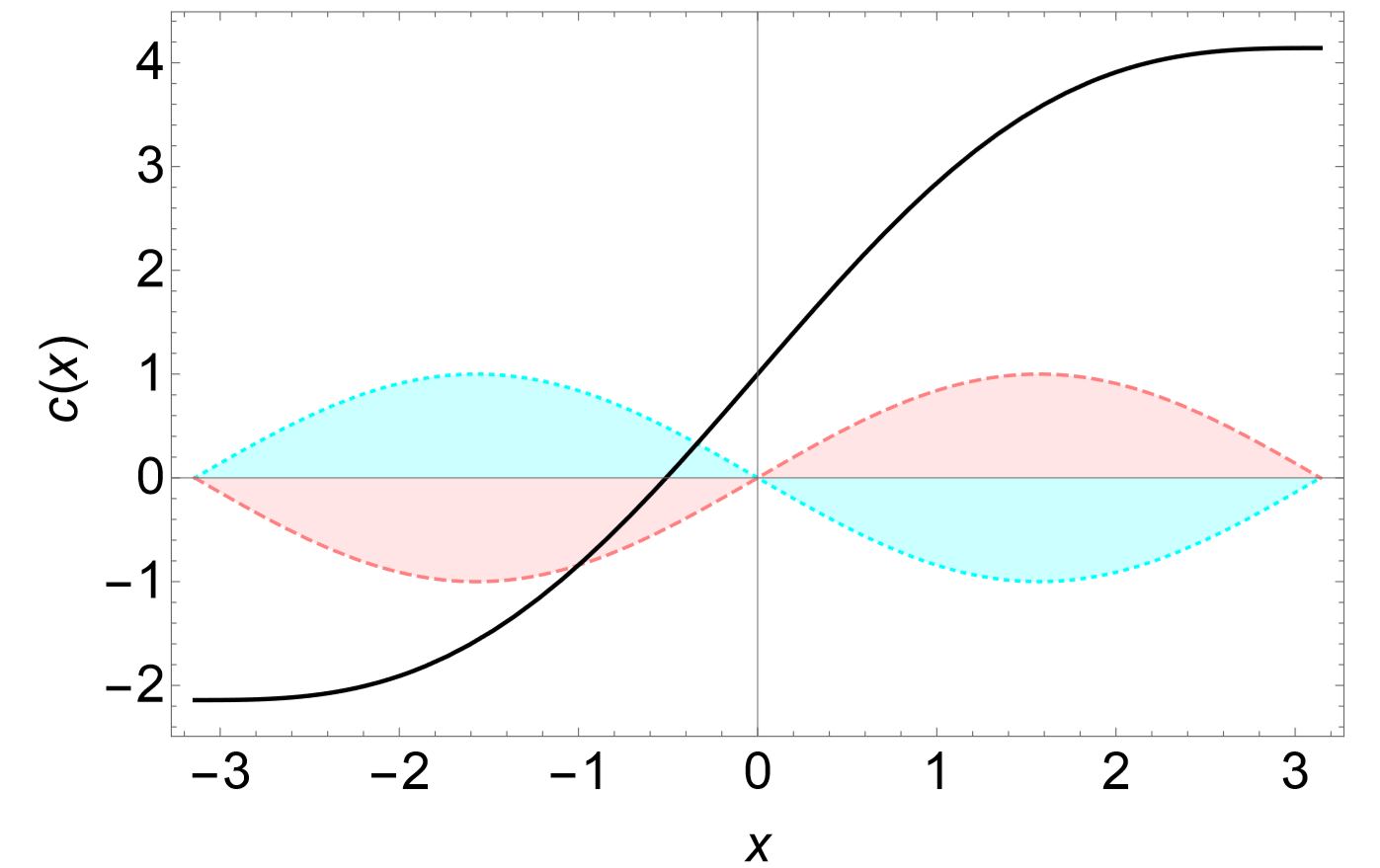
Obtener los estados de equilibrio del siguiente modelo de campo continuo en un espacio 1-D:
\[ ∂c/∂t = D∇^{2}c + 1−x^2 \label{(14.9)} \]
Como vemos anteriormente, los estados de equilibrio de un modelo de campo continuo pueden ser espacialmente heterogéneos. Pero suele darse el caso de que los investigadores están más interesados en estados de equilibrio homogéneos, es decir, estados espacialmente “flat” que pueden permanecer estacionarios con el tiempo. Esto se debe a que, al estudiar la estabilidad de los estados de equilibrio homogéneos, se puede entender si un sistema distribuido espacialmente puede permanecer homogéneo o selforganizar para formar patrones no homogéneos espontáneamente.
Calcular estados de equilibrio homogéneos es mucho más fácil que calcular estados de equilibrio general. Solo necesitas sustituir las funciones de estado del sistema por constantes, lo que hará que todas las derivadas (tanto temporales como espaciales) se conviertan en cero. Por ejemplo, considere obtener estados de equilibrio homogéneos del siguiente modelo de formación de patrones de Turing:
\[ \frac{\partial{u}}{\partial{t}} =a(u-h)+b(v-k) +D_{u}\nabla^{2}u \label{(14.10)} \]
\[ \frac{\partial{v}}{\partial{t}} =c(u-h)+d(v-k) +D_{v}\nabla^{2}v \label{(14.11)} \]
Lo único que hay que hacer es reemplazar las funciones espacio-temporales\( u(x,t)\) y\(v(x,t)\) con las constantes\(u_eq\) y\(v_eq\), respectivamente:
\[ \frac{\partial{u_{eq}}}{\partial{t}} =a({u_{eq}}-h)+b({v_{eq}}-k) +D_{u}\nabla^{2}{u_{eq}} \label{(14.12)} \]
\[ \frac{\partial{v_{eq}}}{\partial{t}} =c({u_{eq}}-h)+d({v_{eq}}-k) +D_{v}\nabla^{2}{v_{eq}} \label{(14.13)} \]
Obsérvese que, dado que\({u_{eq}}\) y ya\({v_{eq}}\) no dependen ni del tiempo ni del espacio, las derivadas temporales del lado izquierdo y las laplacianas del lado derecho ambas desaparecen. Luego obtenemos lo siguiente:
\[ 0 =a({u_{eq}}-h)+b({v_{eq}}-k) \label{(14.14)} \]
\[ 0 =c({u_{eq}}-h)+d({v_{eq}}-k) \label{(14.15)} \]
Al resolver estas ecuaciones, obtenemos\((u_{eq},v_{eq}) = (h,k)\), como esperábamos.
Obsérvese que ahora podemos representar este estado de equilibrio como un “punto” en un espacio\((u,v)\) vectorial bidimensional. Esta es otra razón por la que vale la pena considerar estados de equilibrio homogéneos; proporcionan un punto de referencia más simple y de baja dimensión para ayudarnos a comprender la dinámica de fenómenos espaciales por lo demás complejos. Por lo tanto, también nos centraremos en el análisis de estados de equilibrio homogéneos para lo que resta de este capítulo.
Obtener estados de equilibrio homogéneos del siguiente modelo “Oregonator”:
\[\epsilon \frac{\partial{u}}{\partial{t}} =u(1-u) -\frac{u-q}{u+q}fv +D_{u}{\nabla^{2}}u \label{(14.16)} \]
\[\frac{\partial{v}}{\partial{t}} =u-v +D_{v}\nabla^{2}v \label{(14.17)} \]
Obtener estados de equilibrio homogéneos del siguiente modelo de Keller-Segel:
\[\frac{\partial{a}}{\partial{t}} =\mu\nabla^{2}a -\chi{\nabla} \cdot(a\nabla{c}) \label{(14.18)} \]
\[\frac{\partial{c}}{\partial{t}} =D\nabla^{2}c +fa -kc \label{(14.19)} \]

