8.8: Aplicaciones
- Page ID
- 119253
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Ver no dimensionalización en YouTube
8.8.1. Circuito RLC

Considere una resistencia\(R\), un inductor\(L\) y un condensador\(C\) conectados en serie como se muestra en la Fig. 8.1. Un generador de CA proporciona una fuerza electromotriz variable en el tiempo (EMF)\(\mathcal{E}(t)\),, al circuito. Aquí, determinamos la ecuación diferencial satisfecha por la carga en el condensador.
Las ecuaciones constitutivas para las caídas de voltaje a través de un condensador, una resistencia y un inductor están dadas por
\[V_{C}=q / C, \quad V_{R}=i R, \quad V_{L}=\frac{d i}{d t} L, \nonumber \]
donde\(C\) esta la capacitancia,\(R\) es la resistencia, y\(L\) es la inductancia. El cargo\(q\) y la corriente\(i\) están relacionados por
\[i=\frac{d q}{d t} . \nonumber \]
La ley de voltaje de Kirchhoff establece que el\(\operatorname{emf} \mathcal{E}\) aplicado a cualquier bucle cerrado es igual a la suma de las caídas de voltaje en ese bucle. Aplicar la ley de tensión de Kirchhoff al\(R L C\) ciruit da como resultado
\[V_{L}+V_{R}+V_{C}=\mathcal{E}(t) \label{8.32}\]
o usando la Ecuación\ ref {8.30} y la Ecuación\ ref {8.31},
\[L \frac{d^{2} q}{d t^{2}}+R \frac{d q}{d t}+\frac{1}{C} q=\mathcal{E}(t) \nonumber \]
La ecuación para el\(R L C\) circuito es una ecuación diferencial lineal no homogénea de segundo orden con coeficientes constantes.
El\(A C\) voltaje se puede escribir como\(\mathcal{E}(t)=\mathcal{E}_{0} \cos \omega t\), y la ecuación gobernante para se\(q=q(t)\) puede escribir como
\[\frac{d^{2} q}{d t^{2}}+\frac{R}{L} \frac{d q}{d t}+\frac{1}{L C} q=\frac{\mathcal{E}_{0}}{L} \cos \omega t \label{8.33}\]
Se mostrará la no dimensionalización de esta ecuación para reducir el número de parámetros libres.
Para construir variables adimensionales, primero definimos la frecuencia natural de oscilación de un sistema para que sea la frecuencia de oscilación en ausencia de fuerzas impulsoras o amortiguadoras. El ejemplo icónico es el simple oscilador armónico, con ecuación dada por
\[\ddot{x}+\omega_{0}^{2} x=0, \nonumber \]
y solución general dada por\(x(t)=A \cos \omega_{0} t+B \sin \omega_{0} t\). Aquí, la frecuencia natural de oscilación es\(\omega_{0}\), y el período de oscilación es\(T=2 \pi / \omega_{0}\). Para el\(R L C\) circuito, la frecuencia natural de oscilación se encuentra a partir del coeficiente del\(q\) término, y viene dada por
\[\omega_{0}=\frac{1}{\sqrt{L C}} \nonumber \]
Haciendo uso de\(\omega_{0}\), con unidades de uno en el tiempo, podemos definir un tiempo adimensional\(\tau\) y una carga adimensional\(Q\) mediante
\[\tau=\omega_{0} t, \quad Q=\frac{\omega_{0}^{2} L}{\mathcal{E}_{0}} q \label{8.34}\]
La ecuación adimensional resultante para el\(R L C\) circuito viene dada por
\[\frac{d^{2} Q}{d \tau^{2}}+\alpha \frac{d Q}{d \tau}+Q=\cos \beta \tau \nonumber \]
donde\(\alpha\) y\(\beta\) son parámetros adimensionales dados por
\[\alpha=\frac{R}{L \omega_{0}}, \quad \beta=\frac{\omega}{\omega_{0}} . \nonumber \]
Observe que los cinco parámetros originales en la Ecuación\ ref {8.33}, es decir\(R, L, C, \mathcal{E}_{0}\) y\(\omega\), se han reducido a los dos parámetros adimensionales\(\alpha\) y\(\beta\). Volveremos más adelante para resolver la Ecuación\ ref {8.34} luego de visitar dos aplicaciones más que se demostrarán gobernadas por la misma ecuación adimensional.

8.8.2. Masa en un muelle
Ver misa en primavera en YouTube
Considera una masa conectada por un muelle a una pared fija, con la vista superior mostrada en la Fig. 8.2. La fuerza del resorte está modelada por la ley de Hooke,\(F_{s}=-k x\), y la fricción deslizante se modela como\(F_{f}=-c d x / d t\). Se aplica una fuerza externa y se supone que es sinusoidal, con\(F_{e}=F_{0} \cos \omega t\). La ecuación de Newton,\(F=m a\), resulta en
\[m \frac{d^{2} x}{d t^{2}}=-k x-c \frac{d x}{d t}+F_{0} \cos \omega t \nonumber \]
Reordenando términos, obtenemos
\[\frac{d^{2} x}{d t^{2}}+\frac{c}{m} \frac{d x}{d t}+\frac{k}{m} x=\frac{F_{0}}{m} \cos \omega t \nonumber \]
Aquí, la frecuencia natural de oscilación viene dada por
\[\omega_{0}=\sqrt{\frac{k}{m}} \nonumber \]
y definimos un tiempo adimensional\(\tau\) y una posición\(X\) adimensional
\[\tau=\omega_{0} t, \quad X=\frac{m \omega_{0}^{2}}{F_{0}} x . \nonumber \]
La ecuación adimensional resultante viene dada por
\[\frac{d^{2} X}{d \tau^{2}}+\alpha \frac{d X}{d \tau}+X=\cos \beta \tau \label{8.35}\]
donde aquí,\(\alpha\) y\(\beta\) son parámetros adimensionales dados por
\[\alpha=\frac{c}{m \omega_{0}}, \quad \beta=\frac{\omega}{\omega_{0}} . \nonumber \]
Observe que aunque el problema físico es diferente, y las variables adimensionales se definen de manera diferente, la ecuación adimensional resultante Ecuación\ ref {8.35} para el sistema masa-resorte es la misma que para el\(R L C\) circuito Ecuación\ ref {8.34}.
8.8.3. Péndulo
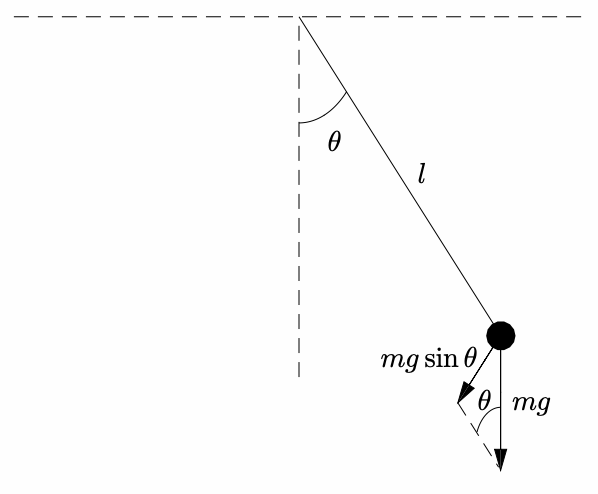
Aquí, consideramos una masa que está unida a una varilla rígida sin masa y está restringida a moverse a lo largo de un arco de círculo centrado en el punto de pivote (ver Fig. 8.3). Supongamos que\(l\) es la longitud fija de la biela, y\(\theta\) es el ángulo que hace con la vertical.
Podemos aplicar la ecuación de Newton,\(F=m a\), a la masa con origen en la parte inferior y eje a lo largo del arco con dirección positiva hacia la derecha. La posición\(s\) de la masa a lo largo del arco viene dada por\(s=l \theta\). La fuerza gravitacional relevante sobre el péndulo es la componente a lo largo del arco, y de la Fig. \(8.3\)se observa que es
\[F_{g}=-m g \sin \theta \nonumber \]
Modelamos la fricción para que sea proporcional a la velocidad del péndulo a lo largo del arco, es decir
\[F_{f}=-c \dot{s}=-c l \dot{\theta} \nonumber \]
Con una fuerza externa sinusoidal,\(F_{e}=F_{0} \cos \omega t\), La ecuación de Newton\(m \ddot{s}=F_{g}+F_{f}+\)\(F_{e}\) da como resultado
\[m l \ddot{\theta}=-m g \sin \theta-c l \dot{\theta}+F_{0} \cos \omega t . \nonumber \]
Reescribiendo, tenemos
\[\ddot{\theta}+\frac{c}{m} \dot{\theta}+\frac{g}{l} \sin \theta=\frac{F_{0}}{m l} \cos \omega t . \nonumber \]
A pequeñas amplitudes de oscilación, podemos aproximarnos\(\sin \theta \approx \theta\), y la frecuencia natural de oscilación\(\omega_{0}\) de la masa viene dada por
\[\omega_{0}=\sqrt{\frac{\bar{g}}{l}} \nonumber \]
Tiempo de no dimensionalización como\(\tau=\omega_{0} t\), la ecuación del péndulo adimensional se convierte
\[\frac{d^{2} \theta}{d \tau^{2}}+\alpha \frac{d \theta}{d \tau}+\sin \theta=\gamma \cos \beta \tau \nonumber \]
donde\(\alpha, \beta\), y\(\gamma\) son parámetros adimensionales dados por
\[\alpha=\frac{c}{m \omega_{0}}, \quad \beta=\frac{\omega}{\omega_{0}}, \quad \gamma=\frac{F_{0}}{m l \omega_{0}^{2}} \nonumber \]
La no linealidad de la ecuación del péndulo, con el término\(\sin \theta\), da como resultado el parámetro adimensional adicional\(\gamma\). Para una pequeña amplitud de oscilación, sin embargo, podemos escalar\(\theta\) por\(\theta=\gamma \Theta\), y la ecuación adimensional de pequeña amplitud se convierte en
\[\frac{d^{2} \Theta}{d \tau^{2}}+\alpha \frac{d \Theta}{d \tau}+\Theta=\cos \beta \tau \label{8.36}\]
la misma ecuación que la Ecuación\ ref {8.34} y la Ecuación\ ref {8.35}.


