5.3: Funciones Heaviside y Dirac Delta
- Page ID
- 116902
La técnica de transformación de Laplace se vuelve realmente útil a la hora de resolver odas con términos discontinuos o impulsivos no homogéneos, estos términos comúnmente modelados usando funciones delta Heaviside o Dirac. Discutiremos estas funciones a su vez, así como sus transformaciones de Laplace.
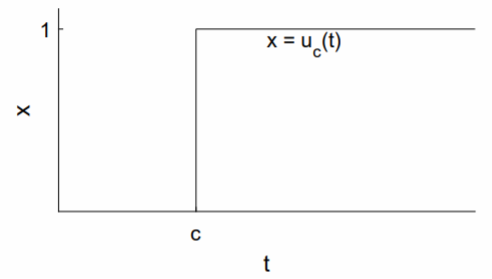
Función Heaviside
La función Heaviside o paso de unidad (ver Fig. \(\PageIndex{1}\)), denotado aquí por\(u_c(t)\), es cero para\(t < c\) y es uno para\(t ≥ c\); es decir, \[\label{eq:1}u_c(t)=\left\{\begin{array}{rl}0,&t<c; \\ 1,&t\geq c.\end{array}\right.\]
El valor preciso de\(u_c(t)\) en un solo punto no\(t = c\) debería importar.
La función Heaviside se puede ver como la función de aumento. La función de reducción (uno para\(t < c\) y cero para\(t ≥ c\)) se define como \[\label{eq:2}1-u_c(t)=\left\{\begin{array}{rl}1,&t<c; \\ 0,&t\geq c.\end{array}\right.\]
La función de escalón ascendente y descendente (cero para\(t < a\), uno para\(a ≤ t < b\) y cero para\(t ≥ b\)) se define como \[\label{eq:3}u_a(t)-u_b(t)=\left\{\begin{array}{rl}0,&t<a; \\ 1,&a\leq t<b; \\ 0,&t\geq b.\end{array}\right.\]
La transformación de Laplace de la función Heaviside está determinada por la integración:
\[\begin{aligned}\mathcal{L}\{u_c(t)\}&=\int_0^{\infty}e^{-st}u_c(t)dt \\ &=\int_c^{\infty}e^{-st}dt \\ &=\frac{e^{-cs}}{s},\end{aligned}\]y se da en la línea 12 del Cuadro 5.1.1.
La función Heaviside se puede utilizar para representar una traslación de una función a\(f(t)\) una distancia\(c\) en la\(t\) dirección positiva. Tenemos\[u_c(t)f(t-c)=\left\{\begin{array}{rl}0,&t<c; \\ f(t-c),&t\geq c.\end{array}\right.\nonumber\]
La transformación de Laplace es\[\begin{aligned}\mathcal{L}\{u_c(t)f(t-c)\}&=\int_0^{\infty}e^{-st}u_c(t)f(t-c)dt \\ &=\int_c^{\infty}e^{-st}f(t-c)dt \\ &=\int_0^{\infty}e^{-s(t'+c)}f(t')dt' \\ &=e^{-cs}\int_0^{\infty}e^{-st'}f(t')dt' \\ &=e^{-cs}F(s),\end{aligned}\] donde hemos cambiado las variables\(t' = t − c\). La traslación de\(f(t)\) una distancia\(c\) en la\(t\) dirección positiva corresponde a la multiplicación de\(F(s)\) por lo exponencial\(e^{−cs}\). Este resultado se muestra en la línea 13 del Cuadro 5.1.1.
Los términos no homogéneos definidos por partes se pueden modelar usando funciones Heaviside. Por ejemplo, considere el caso general de una función por partes definida en dos intervalos:
\[f(t)=\left\{\begin{array}{rl}f_1(t),&\text{if }t<c; \\ f_2(t),&\text{if }t\geq c.\end{array}\right.\nonumber\]
Usando la función Heaviside\(u_c\), la función se\(f(t)\) puede escribir en una sola línea como\[f(t)=f_1(t)+(f_2(t)-f_1(t))u_c(t).\nonumber\]
Este ejemplo se puede generalizar a funciones por partes definidas en múltiples intervalos.
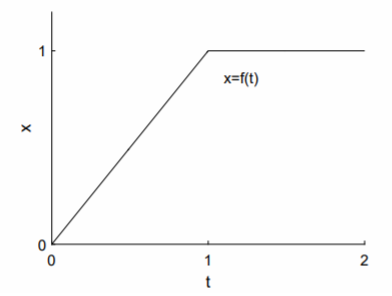
Como ejemplo concreto, supongamos que el término no homogéneo está representado por una función linealmente creciente, que luego se convierte en una función constante, como se esboza en la Fig. \(\PageIndex{2}\). Explícitamente,\[f(t)=\left\{\begin{array}{rl}t,&\text{if }t<1; \\ 1,&\text{if }t\geq 1.\end{array}\right.\nonumber\]
Podemos reescribir\(f(t)\) usando la función Heaviside\(u_1(t)\):
\[f(t)=t-u_1(t)(t-1);\nonumber\]y podemos tomar la transformación de Laplace de la función\(f(t)\) escribiendo\[F(s)=\mathcal{L}\{t\}-\mathcal{L}\{u_1(t)(t-1)\}.\nonumber\]
La transformada de Laplace del primer término se encuentra a partir de la línea 4 de la tabla, y la transformada de Laplace del segundo término se encuentra a partir de una combinación de la línea 13 y la línea 4. Tenemos\[F(s)=\frac{1}{s^2}-\frac{e^{-s}}{s^2}.\nonumber\]
Función Dirac Delta
La función delta de Dirac, denotada como\(\delta (t)\), se define exigiendo que para cualquier función\(f(t)\),\[\int_{-\infty}^{\infty}f(t)\delta(t)dt=f(0).\nonumber\]
La visión habitual de la función delta de Dirac desplazada\(\delta (t − c)\) es que es cero en todas partes excepto en\(t = c\), donde es infinita, y la integral sobre la función delta de Dirac es una. La función delta de Dirac no es técnicamente una función, sino que es lo que los matemáticos llaman una distribución. Sin embargo, en la mayoría de los casos de interés práctico, puede tratarse como una función, donde se obtienen resultados físicos después de una integración final.
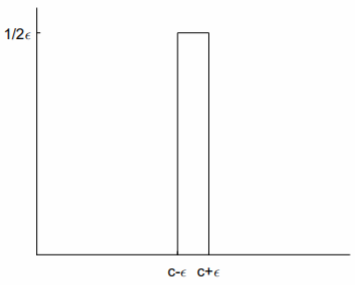
Hay muchas maneras de representar la función delta de Dirac como un límite de una función bien definida. Para nuestros propósitos, la representación más útil hace uso de la función step-up, step-down de\(\eqref{eq:3}\) (ver Fig. \(\PageIndex{3}\)):
\[\delta(t-c)=\underset{\epsilon\to 0}{\lim}\frac{1}{2\epsilon}(u_{c-\epsilon}(t)-u_{c+\epsilon}(t)).\nonumber\]
Antes de tomar el límite, la función step-up, step-down bien definida es cero excepto en un pequeño intervalo de ancho\(2\epsilon\) centrado en\(t = c\), sobre el cual toma el valor grande\(1/2\epsilon\). La integral de esta función es una, independiente del valor de\(\epsilon\).
La transformación de Laplace de la función delta Dirac se encuentra fácilmente mediante la integración usando la definición de la función delta:
\[\begin{aligned}\mathcal{L}\{\delta (t-c)\}&=\int_0^{\infty}e^{-st}\delta (t-c)dt \\ &=e^{-cs}.\end{aligned}\]
Este resultado se muestra en la línea 14 del Cuadro 5.1.1.