8.1: Puntos Fijos y Estabilidad
- Page ID
- 116974
Una Dimensión
Considere la ecuación diferencial unidimensional para\(x = x(t)\) dada por \[\label{eq:1}\overset{.}{x}=f(x).\]
Decimos que\(x_*\) es un punto fijo, o punto de equilibrio, de\(\eqref{eq:1}\) si\(f(x_*) = 0\). En el punto fijo,\(\overset{.}{x} = 0\). Se utiliza la terminología punto fijo ya que la solución a\(\eqref{eq:1}\) con condición inicial\(x(0) = x_*\) es\(x(t) = x_*\) para siempre\(t\).
Un punto fijo, sin embargo, puede ser estable o inestable. Se dice que un punto fijo es estable si una pequeña perturbación de la solución desde el punto fijo decae en el tiempo; se dice que es inestable si una pequeña perturbación crece en el tiempo. Podemos determinar la estabilidad mediante un análisis lineal. Let\(x = x_* +\epsilon (t)\), donde\(\epsilon\) representa una pequeña perturbación de la solución desde el punto fijo\(x_*\). Porque\(x_*\) es una constante,\(\overset{.}{x}=\overset{.}{\epsilon}\); y porque\(x_*\) es un punto fijo,\(f(x_*) = 0\). Serie Taylor expandiéndose sobre\(\epsilon = 0\), tenemos\[\begin{aligned}\overset{.}{\epsilon}&=f(x_*+\epsilon) \\ &=f(x_*)+\epsilon f'(x_*)+\ldots \\ &=\epsilon f'(x_*)+\ldots\end{aligned}\]
Los términos omitidos en la expansión de la serie Taylor son proporcionales a\(\epsilon^2\), y pueden hacerse despreciables en un corto intervalo de tiempo con respecto al término guardado, proporcionales a\(\epsilon\), tomando\(\epsilon (0)\) suficientemente pequeños. Por lo tanto, al menos en tiempos cortos, la ecuación diferencial a considerar\(\overset{.}{\epsilon}= f ' (x_*)\epsilon\), es lineal y tiene por ahora la solución familiar\[\epsilon (t)=\epsilon (0)e^{f'(x_*)t}.\nonumber\]
La perturbación de la solución de punto fijo decae\(x(t) = x_*\) así exponencialmente si\(f' (x_*) < 0\), y decimos que el punto fijo es estable. Si\(f' (x_*) > 0\), la perturbación crece exponencialmente y decimos que el punto fijo es inestable. Si\(f' (x_*) = 0\), decimos que el punto fijo es marginalmente estable, y se debe considerar el siguiente término de orden superior en la expansión de la serie Taylor.
Encuentra todos los puntos fijos de la ecuación logística\(\overset{.}{x} = x(1 − x)\) y determina su estabilidad.
Solución
Hay dos puntos fijos en los que\(\overset{.}{x} = 0\), dado por\(x_* = 0\) y\(x_* = 1\). La estabilidad de estos puntos de equilibrio se puede determinar considerando la derivada de\(f(x) = x(1 − x)\). Tenemos\(f' (x) = 1 − 2x\). Por lo\(f' (0) = 1 > 0\) tanto, entonces ese\(x_* = 0\) es un punto fijo inestable, y\(f' (1) = −1 < 0\) así ese\(x_* = 1\) es un punto fijo estable. En efecto, previamente hemos encontrado que todas las soluciones se acercan asintóticamente al punto fijo estable.
Dos Dimensiones
La idea de puntos fijos y estabilidad puede extenderse a sistemas de odas de orden superior. Aquí, consideramos un sistema bidimensional y necesitaremos hacer uso de la expansión bidimensional de la serie Taylor de una función\(F(x, y)\) sobre el origen. En general, la serie Taylor de\(F(x, y)\) viene dada por\[F(x,y)=F+x\frac{\partial F}{\partial x}+y\frac{\partial F}{\partial y}+\frac{1}{2}\left(x^2\frac{\partial ^2F}{\partial x^2}+2xy\frac{\partial ^2F}{\partial x\partial y}+y^2\frac{\partial^2F}{\partial y^2}\right)+\ldots,\nonumber\] donde la función\(F\) y todas sus derivadas parciales en el lado derecho se evalúan en el origen. Tenga en cuenta que la serie Taylor está construida de manera que todas las derivadas parciales del lado izquierdo coincidan con las del lado derecho en el origen.
Consideramos ahora el sistema bidimensional dado por \[\label{eq:2}\overset{.}{x}=f(x,y),\quad\overset{.}{y}=g(x,y).\]
\((x_*, y_*)\)Se dice que el punto es un punto fijo de\(\eqref{eq:2}\) si\(f(x_*, y_*) = 0\) y\(g(x_*, y_*) = 0\). Nuevamente, la estabilidad local de un punto fijo se puede determinar mediante un análisis lineal. Dejamos\(x(t) = x_* + \epsilon (t)\) y\(y(t) = y_* + \delta (t)\), donde\(\epsilon\) y\(\delta\) son pequeñas perturbaciones independientes desde el punto fijo. Haciendo uso de la serie Taylor bidimensional de\(f(x, y)\) y\(g(x, y)\) sobre el punto fijo, o equivalentemente sobre\((\epsilon , \delta ) = (0, 0)\), tenemos\[\begin{aligned}\overset{.}{\epsilon}&=f(x_*+\epsilon ,y_*+\delta ) \\ &=f+\epsilon\frac{\partial f}{\partial x}+\delta\frac{\partial f}{\partial y}+\ldots \\ &=\epsilon\frac{\partial f}{\partial x}+\delta\frac{\partial f}{\partial y}+\ldots \\ \delta &=g(x_*+\epsilon ,y_*+\delta ) \\ &=g+\epsilon\frac{\partial g}{\partial x}+\delta\frac{\partial g}{\partial y}+\ldots \\ &=\epsilon\frac{\partial g}{\partial x}+\delta\frac{\partial g}{\partial y}+\ldots,\end{aligned}\]
donde en la serie Taylor\(f,\: g\) y todas sus derivadas parciales se evalúan en el punto fijo\((x_*, y_*)\). Despreciando términos de orden superior en la serie Taylor, tenemos así un sistema de odas para la perturbación, dado en forma de matriz como \[\label{eq:3}\frac{d}{dt}\left(\begin{array}{c}\epsilon \\ \delta\end{array}\right)=\left(\begin{array}{cc}\frac{\partial f}{\partial x}&\frac{\partial f}{\partial y} \\ \frac{\partial g}{\partial x}&\frac{\partial g}{\partial y}\end{array}\right)\left(\begin{array}{c}\epsilon \\ \delta\end{array}\right).\]
La matriz de dos por dos en\(\eqref{eq:3}\) se llama la matriz jacobiana en el punto fijo. Un análisis de valores propios de la matriz jacobiana normalmente dará dos valores propios\(\lambda_1\) y\(\lambda_2\). Estos valores propios pueden ser reales y distintos, pares conjugados complejos o repetidos. El punto fijo es estable (todas las perturbaciones decaen exponencialmente) si ambos valores propios tienen partes reales negativas. El punto fijo es inestable (algunas perturbaciones crecen exponencialmente) si al menos uno de los valores propios tiene una parte real positiva. Los puntos fijos se pueden clasificar además como nodos estables o inestables, puntos de sillín inestables, puntos espirales estables o inestables, o nodos inestables o inestables.
Encontrar todos los puntos fijos del sistema no lineal\(\overset{.}{x}= x(3 − x − 2y)\),\(\overset{.}{y} = y(2 − x − y)\), y determinar su estabilidad.
Solución
Los puntos fijos se determinan resolviendo\[f(x,y)=x(3-x-2y)=0,\quad g(x,y)=y(2-x-y)=0.\nonumber\]
Evidentemente,\((x, y) = (0, 0)\) es un punto fijo. Por un lado, aunque sólo sea\(x = 0\), entonces la ecuación\(g(x, y) = 0\) rinde\(y = 2\). Por otro lado, aunque sólo sea\(y = 0\), entonces la ecuación\(f(x, y) = 0\) rinde\(x = 3\). Si ambos\(x\) y\(y\) son distintos de cero, entonces debemos resolver el sistema lineal\[x+2y=3,\quad x+y=2,\nonumber\]
y la solución se encuentra fácilmente para ser\((x, y) = (1, 1)\). De ahí que hayamos determinado los cuatro puntos fijos\((x_*, y_*) = (0, 0),\: (0, 2),\: (3, 0),\: (1, 1)\). La matriz jacobiana viene dada por\[\left(\begin{array}{cc}\frac{\partial f}{\partial x}&\frac{\partial f}{\partial y} \\ \frac{\partial g}{\partial x}&\frac{\partial g}{\partial y}\end{array}\right)=\left(\begin{array}{cc}3-2x-2y & -2x \\ -y&2-x-2y\end{array}\right).\nonumber\]
La estabilidad de los puntos fijos puede considerarse a su vez. Con\(\mathbf{J}_*\) la matriz jacobiana evaluada en el punto fijo, tenemos\[(x_*, y_*)=(0,0)\: :\quad\mathbf{J}_* =\left(\begin{array}{cc}3&0 \\ 0&2\end{array}\right).\nonumber\]
Los valores propios de\(\mathbf{J}_*\) son\(\lambda = 3,\: 2\) para que el punto fijo\((0, 0)\) sea un nodo inestable. Siguiente,\[(x_*, y_*)=(0,2)\: :\quad\mathbf{J}_*=\left(\begin{array}{cc}-1&0 \\ -2&-2\end{array}\right).\nonumber\]
Los valores propios de\(\mathbf{J}_*\) son\(\lambda = −1,\: −2\) para que el punto fijo\((0, 2)\) sea un nodo estable. Siguiente,\[(x_*, y_*)=(3,0)\: :\quad\mathbf{J}_*=\left(\begin{array}{cc}-3&-6 \\ 0&-1\end{array}\right).\nonumber\]
Los valores propios de\(\mathbf{J}_*\) son\(\lambda = −3,\: −1\) para que el punto fijo\((3, 0)\) sea también un nodo estable. Por último,\[(x_*, y_*)=(1,1)\: :\quad\mathbf{J}_*=\left(\begin{array}{cc}-1&-2 \\ -1&-1\end{array}\right).\nonumber\]
La ecuación característica de\(\mathbf{J}_*\) viene dada por\((−1 − \lambda )^2 − 2 = 0\), así que eso\(\lambda = −1 ± \sqrt{2}\). Dado que un valor propio es negativo y el otro positivo, el punto fijo\((1, 1)\) es un punto de sillín inestable. A partir de nuestro análisis de los puntos fijos, se puede esperar que todas las soluciones sean asíntotas a uno de los puntos fijos estables\((0, 2)\) o\((3, 0)\), dependiendo de las condiciones iniciales.
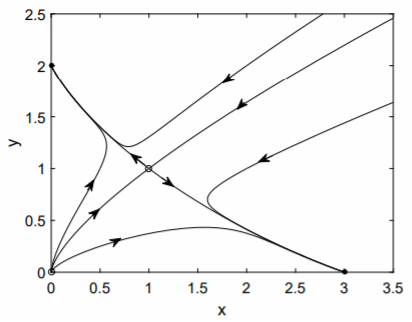
Es de interés esbozar el retrato de fase para este sistema no lineal. Los vectores propios asociados con el punto de sillín inestable\((1, 1)\) determinan las direcciones del flujo hacia y desde este punto fijo. El vector propio asociado con el valor propio positivo se\(\lambda_1 = −1 +\sqrt{2}\) puede determinar a partir de la primera ecuación de\((\mathbf{J}_* − \lambda_1\mathbf{I})\mathbf{v_1 }= 0\), o\[-\sqrt{2}v_{11}-2v_{12}=0,\nonumber\] así que\(v_{12} = −(\sqrt{2}/2)v_{11}\). El vector propio asociado con el valor propio negativo\(\lambda_1 = −1 −\sqrt{2}\) satisface\(v_{22} = (\sqrt{2}/2)v_{21}\). Los vectores propios dan la pendiente de las líneas con origen en el punto fijo para trayectorias entrantes (valor propio negativo) y salientes (valor propio positivo). Las trayectorias salientes tienen pendiente negativa\(−\sqrt{2}/2\) y las trayectorias entrantes tienen pendiente positiva\(\sqrt{2}/2\). Un boceto aproximado del retrato de fase se puede hacer a mano (como se demuestra en clase). Aquí, una gráfica generada por computadora obtenida a partir de la solución numérica de las odas acopladas no lineales se presenta en la Fig. \(\PageIndex{1}\). La curva que comienza desde el origen y en el infinito, y que termina en el punto inestable de la silla de montar se llama separatriz. Esta curva separa el espacio de fase en dos regiones: condiciones iniciales para las cuales la solución asintota al punto fijo\((0, 2)\), y condiciones iniciales para las que la solución asíntota al punto fijo\((3, 0)\).


