9.1: Derivación de la Ecuación de Difusión

Última actualización
Guardar como PDF

Page ID: 116971

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Para derivar la ecuación de difusión en una dimensión espacial, imaginamos un quieto líquido en una tubería larga de área transversal constante. Se coloca una pequeña cantidad de tinte en una sección transversal de la tubería y se deja que se difumine hacia arriba y hacia abajo de la tubería. El colorante se difunde de regiones de mayor concentración a regiones de menor concentración.

Definimos\(u(x, t)\) que es la concentración del tinte en posición a\(x\) lo largo de la tubería, y deseamos encontrar el pde satisfecho por\(u\). Es útil realizar un seguimiento de las unidades de las diversas cantidades involucradas en la derivación e introducimos la notación de corchete\([X]\) para significar las unidades de\(X\). Las unidades dimensionales relevantes utilizadas en la derivación de la ecuación de difusión son masa\(m\)\(l\), longitud y tiempo\(t\). Suponiendo que la concentración de tinte es uniforme en cada sección transversal de la tubería, las dimensiones de concentración utilizadas aquí son\([u] = m/l\).

La masa de tinte en el volumen del tubo infinitesimal ubicado entre la posición\(x_1\) y la posición\(x_2\) en el tiempo\(t\), con\(x_1 < x < x_2\), se da al orden\(\Delta x = x_2 − x_1\) por\[M=u(x,t)\Delta x.\nonumber\]

La masa de tinte en este volumen de tubo infinitesimal cambia por difusión dentro y fuera de los extremos de sección transversal situados en posición\(x_1\) y\(x_2\) (Figura\(\PageIndex{1}\)). Suponemos que la velocidad de difusión es proporcional al gradiente de concentración, una relación conocida como ley de difusión de Fick. La ley de difusión de Fick asume el flujo másico\(J\), con unidades\([J] = m/t\) a través de una sección transversal de la tubería viene dada por \[\label{eq:1}J=-Du_x,\]donde la constante de difusión\(D > 0\) tiene unidades\([D] = l^2/t\), y hemos utilizado la notación\(u_x = \partial u/\partial x\). El flujo másico es opuesto en signo al gradiente de concentración de manera que el flujo es de alta concentración a baja concentración. La tasa de tiempo de cambio en la masa de tinte entre\(x_1\) y\(x_2\) viene dada por la diferencia entre el flujo másico hacia adentro y el flujo másico fuera de la sección transversal infinitesimal

Figura\(\PageIndex{1}\): Derivación de la ecuación de difusión.

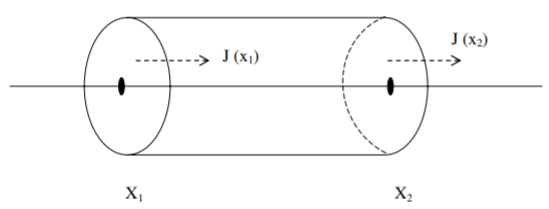
volumen. Un flujo másico positivo significa difusión de izquierda a derecha. Por lo tanto, la tasa de tiempo de cambio de la masa de tinte viene dada por\[\frac{dM}{dt}=J(x_1, t)-J(x_2, t),\nonumber\] o reescritura en términos de\(u(x,t)\):

\[u_t(x,t)\Delta x=D(u_x(x_2,t)-u_x(x_1,t)).\nonumber\]

Dividir por\(\Delta x\) y tomar el límite\(\Delta x\to 0\) da como resultado la ecuación de difusión:

\[u_t=Du_{xx}.\nonumber\]

Observamos que la ecuación de difusión es idéntica a la ecuación de conducción de calor, donde\(u\) está la temperatura, y la constante\(D\) (comúnmente escrita como\(\kappa\)) es la conductividad térmica.