9.2: Derivación de la Ecuación de Onda

Última actualización
Guardar como PDF

Page ID: 116984

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

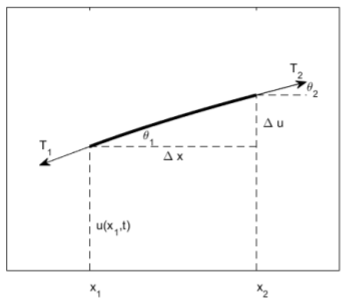
Para derivar la ecuación de onda en una dimensión espacial, imaginamos una cuerda elástica que sufre vibraciones transversales de pequeña amplitud. \(u(x, t)\)Definimos como el desplazamiento vertical de la cadena desde el\(x\) eje -en posición\(x\) y tiempo\(t\), y deseamos encontrar el pde satisfecho por\(u\). \(\rho\)Definimos como la densidad de masa constante de la cuerda,\(T\) la tensión de la cuerda y\(\theta\) el ángulo entre la cuerda y la línea horizontal. Consideramos un elemento de cadena infinitesimal ubicado entre\(x_1\) y\(x_2\), con\(\Delta x = x_2 − x_1\), como se muestra en la Fig. \(\PageIndex{1}\). Las ecuaciones gobernantes son la ley de movimiento de Newton para la aceleración horizontal y vertical de nuestro elemento de cuerda infinitesimal, y asumimos que el elemento string solo acelera verticalmente. Por lo tanto, las fuerzas horizontales deben equilibrarse y tenemos\[T_2\cos\theta_2=T_1\cos\theta_1.\nonumber\]

Las fuerzas verticales dan como resultado una aceleración vertical, y con\(u_{tt}\) la aceleración vertical del elemento de cuerda y\(\rho\sqrt{\Delta x^2+\Delta u^2}=\rho\Delta x\sqrt{1+u_x^2}\) su masa, donde hemos utilizado\(u_x = \Delta u/\Delta x\), exacto como\(\Delta x\to 0\), tenemos\[\rho\Delta x\sqrt{1+u_x^2}u_{tt}=T_2\sin\theta_2-T_1\sin\theta_1.\nonumber\]

Figura\(\PageIndex{1}\): Derivación de la ecuación de onda.

Ahora hacemos la suposición de pequeñas vibraciones, es decir\(\Delta u ≪ \Delta x\), o equivalentemente\(u_x ≪ 1\). Tenga en cuenta\([u] = l\) que para que\(u_x\) sea adimensional. Con esta aproximación, al orden de liderazgo en\(u_x\) tenemos\[\cos\theta_2=\cos\theta_1=1,\nonumber\]\[\sin\theta_2=u_x(x_2,t),\quad\sin\theta_1=u_x(x_1,t),\nonumber\] y\[\sqrt{1+u_x^2}=1.\nonumber\]

Por lo tanto, al orden inicial\(T_1 = T_2 = T\), (es decir, la tensión en la cuerda es aproximadamente constante), y\[\rho\Delta xu_{tt}=T(u_x(x_2,t)-u_x(x_1,t)).\nonumber\]

Dividir por\(\Delta x\) y tomar el límite\(\Delta x\to 0\) da como resultado la ecuación de onda\[u_{tt}=c^2u_{xx},\nonumber\] donde\(c^2=T/\rho\). Desde\([T]=ml/t^2\) y\([\rho]=m/l\), tenemos\([c^2]=l^2/t^2\) así que\(c\) tiene unidades de velocidad.