1.3: Ecuaciones separables
- Page ID
- 115483
Cuando una ecuación diferencial es de la forma\(y' = f(x)\), podemos simplemente integrar:\(y = \int f(x) dx + C\). Desafortunadamente este método ya no funciona para la forma general de la ecuación\(y' = f(x, y)\). Integración de los rendimientos de ambos lados
\[y = \int f(x, y) dx + C \nonumber \]
Observe la dependencia\(y\) en lo integral.
Ecuaciones separables
Supongamos que la ecuación es separable. Es decir, consideremos
\[y' = f(x)g(y), \nonumber \]
para algunas funciones\(f(x)\) y\(g(y)\). Escribamos la ecuación en la notación Leibniz
\[\frac{dy}{dx} = f(x)g(y) \nonumber \]
Luego reescribimos la ecuación como
\[\frac{dy}{g(y)} = f(x) dx \nonumber \]
Ahora ambos lados parecen algo que podemos integrar. Obtenemos
\[\int \frac{dy}{g(y)} = \int f(x) dx + C \nonumber \]
Si podemos encontrar expresiones de forma cerrada para estas dos integrales, podemos, tal vez, resolver para\(y.\)
Toma la ecuación
\[ y' = xy \nonumber \]
Primero tenga en cuenta que\(y = 0\) es una solución, así que asumamos\(y \ne 0\) de ahora en adelante, para que podamos dividirnos por\(y\). Escribe la ecuación como\(\frac{dy}{dx} = xy,\) entonces
\[\int \frac{dy}{y} = \int x dx + C. \nonumber \]
Calculamos los antiderivados para obtener
\[\ln \left \vert y \right \vert = \frac{x^2}{2} + C \nonumber \]
O
\[\left \vert y \right \vert = e^{\frac{x^2}{2}+C} = e^{\frac{x^{2}}{2}}e^{C}= De^{\frac{x^2}{2}} \nonumber \]
donde\(D > 0\) hay alguna constante. Porque\(y = 0\) es una solución y por el valor absoluto realmente podemos escribir:
\[y = De^{\frac{x^2}{2}} \nonumber \]
para cualquier número\(D\) (incluyendo cero o negativo).
Verificamos:
\[y' = Dxe^{\frac{x^2}{2}} = x \left ( De^{\frac{x^2}{2}} \right ) = xy \nonumber \]
¡Yay!
Deberíamos ser un poco más cuidadosos con este método. Puede que te preocupe que nos estuviéramos integrando en dos variables diferentes. Aparentemente hicimos una operación diferente a cada lado. Trabajemos más rigurosamente a través de este método. Toma
\[\frac{dy}{dx} = f(x)g(y) \nonumber \]
Reescribimos la ecuación de la siguiente manera. Tenga en cuenta que\(y = y(x)\) es una función de\(x\) y así es\(\frac{dy}{dx}!\)
\[\frac{1}{g(y)} \frac{dy}{dx} = f(x) \nonumber \]
Integramos ambas partes con respecto a\(x.\)
\[\int \frac{1}{g(y)} \frac{dy}{dx} dx = \int f(x) dx + C \nonumber \]
Usamos la fórmula de cambio de variables (sustitución) en el lado izquierdo:
\[\int \frac{1}{g(y)} dy = \int f(x) dx + C \nonumber \]
Y ya terminamos.
Soluciones implícitas
Está claro que a veces podríamos quedarnos atascados aunque podamos hacer la integración. Por ejemplo, tomemos la ecuación separable
\[y' = \frac{xy}{y^2 + 1} \nonumber \]
Separamos variables,
\[\frac{y^2 + 1}{y} dy = \left ( y + \frac{1}{y} \right ) dy = x dx \nonumber \]
Nos integramos para obtener
\[\frac{y^2}{2} + ln \left \vert y \right \vert = \frac{x^2}{2} + C \nonumber \]
o quizás la expresión más fácil (donde\(D = 2C\))
\[y^2 + 2ln \left \vert y \right \vert = x^2 + D \nonumber \]
No es fácil encontrar la solución explícitamente ya que es difícil de resolver\(y\). Nosotros, por lo tanto, dejamos la solución en esta forma y la llamamos solución implícita. Todavía es fácil comprobar que una solución implícita satisface la ecuación diferencial. En este caso, diferenciamos con respecto a\(x\), y recordamos que\(y\) es una función de\(x\), para obtener
\[y' \left ( 2y + \frac{2}{y} \right ) = 2x \nonumber \]
Multiplica ambos lados por\(y\) y divide por\(2(y^2+1)\) y obtendrás exactamente la ecuación diferencial. Dejamos este cómputo al lector.
Si tienes una solución implícita y quieres calcular valores para\(y\), es posible que tengas que ser complicado. Es posible que obtenga múltiples soluciones\(y\) para cada una\(x\), por lo que debe elegir una. A veces puedes graficar\(x\) en función de\(y\), y luego voltear tu papel. A veces hay que hacer más.
Las computadoras también son buenas en algunos de estos trucos. El software matemático más avanzado suele tener alguna forma de trazar soluciones a ecuaciones implícitas. Por ejemplo, porque\(C=0\) si trazas todos los puntos a los\((x,y)\) que son soluciones\(y^2+2\ln|y|=x^2\), encuentras las dos curvas en Figura\(\PageIndex{1}\). Esto no es del todo un gráfico de una función. Para cada uno\(x\) hay dos opciones de\(y\). Para encontrar una función tendrías que escoger una de estas dos curvas. Tú eliges el que satisfaga tu condición inicial si tienes uno. Por ejemplo, la curva superior satisface la condición\(y(1)=1\). Entonces para cada uno\(C\) realmente obtuvimos dos soluciones. Como puede ver, calcular valores a partir de una solución implícita puede ser algo complicado. Pero a veces, una solución implícita es lo mejor que podemos hacer.
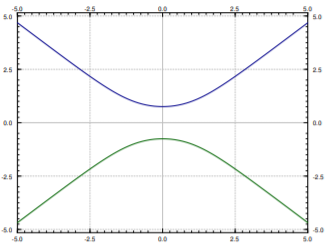
La ecuación anterior también tiene la solución\(y=0\). Entonces la solución general es\[y^2 + 2 \ln \, \lvert y \rvert = x^2 + C, \qquad \text{and} \qquad y=0. \nonumber \] Estas soluciones periféricascomo las que a veces\(y=0\) se llaman soluciones singulares.
Resolver\(x^2y' = 1 - x^2 + y^2 -x^2y^2\),\(y(1) = 0.\)
Solución
Primer factor el lado derecho para obtener
\[x^2y' = \left ( 1- x^2 \right ) \left ( 1 + y^2 \right ) \nonumber \]
Separar variables, integrar y resolver para\(y\)
\[\begin{align}\begin{aligned} \frac{y'}{1 + y^2} &= \frac {1 - x^2}{x^2}, \\ \frac{y'}{1 + y^2} &= \frac {1}{ x^2} -1, \\ \text{arctan}(y) &= -\frac{1}{x^2} - x + C, \\ y &= \tan \left( -\frac{1}{x} - x + C \right )\end{aligned}\end{align} \nonumber \]
Resolver para la condición inicial,\(0 = \tan(-2+C)\) para obtener\(C=2\) (o\(C = 2 + \pi\)\(C = 2 + 2\pi\), o, etc.). La solución particular que buscamos es, por lo tanto,\[y = \tan \left(\frac{-1}{x} - x + 2 \right) . \nonumber \]
Bob hizo una taza de café, y a Bob le gusta tomar café solo una vez alcanza los 60 grados centígrados y no lo quemará. Inicialmente en el tiempo\(t=0\) minutos, Bob midió la temperatura y el café fue de 89 grados centígrados. Un minuto después, Bob volvió a medir el café y tenía 85 grados. La temperatura de la habitación (la temperatura ambiente) es de 22 grados. ¿Cuándo debería empezar a beber Bob?
Solución
Dejar\(T\) ser la temperatura del café en grados Celsius, y dejar que\(A\) sea la temperatura ambiente (ambiente), también en grados Celsios. establece que la velocidad a la que la temperatura del café está cambiando es proporcional a la diferencia entre la temperatura ambiente y la temperatura del café. Es decir,
\[\frac{dT}{dt} = k(A - T), \nonumber \]
para alguna constante\(k\). Para nuestra configuración\( A = 22\),\(T(0) = 89\),\(T(1) = 85\). Separamos variables e integramos (dejar\(C\) y\(D\) denotar constantes arbitrarias)
\[\begin{align}\begin{aligned} \frac{1}{T -A} \frac {dT}{dt} &= -k, \\ \ln (T - A) &= -kt + C, \, \, \, \, \, \left ( \text {note that} T - A > 0 \right ) \\ T - A &= De^{-kt}, \\ T &= A + De^{-kt}\end{aligned}\end{align} \nonumber \]
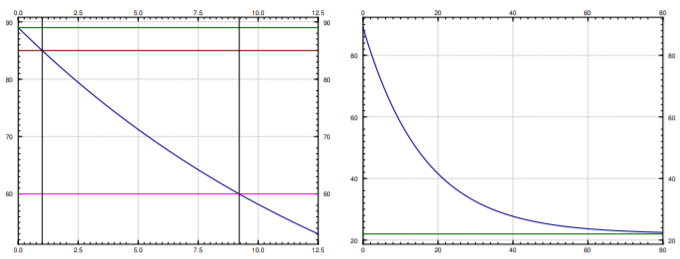
Es decir,\(T = 22 + D\, e^{-kt}\). Enchufamos la primera condición:\(89 = T(0) = 22 + D\), y por lo tanto\(D = 67\). Entonces\(T = 22 + 67\, e^{-kt}\). Dice la segunda condición\(85 = T(1) = 22 + 67\, e^{-k}\). Resolviendo para\(k\) nosotros obtenemos\(k = - \ln \frac{85-22}{67} \approx 0.0616\). Ahora resolvemos por el momento\(t\) que nos da una temperatura de 60 grados. A saber, resolvemos\[60 = 22 + 67 e^{-0.0616t} \nonumber \] obtener\(t = - \frac{\ln \frac{60-22}{67}}{0.0616} \approx 9.21\) minutos. Entonces Bob puede comenzar a tomar el café a poco más de 9 minutos desde el momento en que Bob lo hizo. Eso es probablemente sobre la cantidad de tiempo que nos llevó calcular cuánto tiempo tardaría. Ver Figura\(\PageIndex{2}\).
Encuentre la solución general para\(y' = \frac{-xy^2}{3}\) (incluyendo soluciones singulares).
Solución
Primero tenga en cuenta que\(y=0\) es una solución (una solución singular). Ahora asuma eso\(y \not= 0\). \[\begin{align}\begin{aligned} -\frac {3}{y^2} y' &= x , \\ \frac {3}{y} &= \frac {x^2}{2} + C, \\ y &= \frac {3}{ \frac{x^2}{2} + C} = \frac {6}{x^2 + 2C}.\end{aligned}\end{align} \nonumber \]Entonces la solución general es,\[y=\frac{6}{x^{2}+2C},\quad\text{and}\quad y=0. \nonumber \]


