3.5: Sistemas bidimensionales y sus campos vectoriales
- Page ID
- 115441
Tomemos un momento para hablar de los sistemas homogéneos lineales de coeficiente constante en el plano. Se puede obtener mucha intuición estudiando este sencillo caso. Supongamos que usamos coordenadas\((x,y)\) para el plano como de costumbre, y supongamos que\(P=\left[\begin{array}{cc}{a}&{b}\\{c}&{d}\end{array}\right]\) es una\(2\, \times \, 2\) matriz. Considerar el sistema
\[\label{pln:eq} \begin{bmatrix} x \\ y \end{bmatrix} ' = P \begin{bmatrix} x \\ y \end{bmatrix} \qquad \text{or} \qquad \begin{bmatrix} x \\ y \end{bmatrix} ' = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} . \]
El sistema es autónomo (compare esta sección con la Sección 1.6) y así podemos dibujar un campo vectorial (ver final de la Sección 3.1). Podremos contar visualmente cómo es el campo vectorial y cómo se comportan las soluciones, una vez que encontremos los valores propios y los vectores propios de la matriz\(P\). Para esta sección, suponemos que\(P\) tiene dos valores propios y dos vectores propios correspondientes.
1
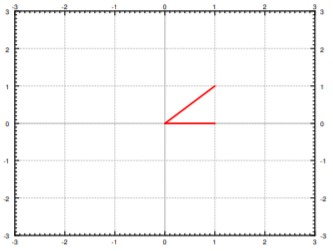
Supongamos que los valores propios de\(P\) son reales y positivos. Encontramos dos vectores propios correspondientes y los trazamos en el plano. Por ejemplo, toma la matriz\( \begin{bmatrix} 1&1 \\ 0&2 \end{bmatrix} \). Los valores propios son 1 y 2 y los vectores propios correspondientes son\( \begin{bmatrix} 1\\0 \end{bmatrix} \) y\( \begin{bmatrix} 1 \\1 \end{bmatrix} \). Ver Figura\(\PageIndex{1}\).
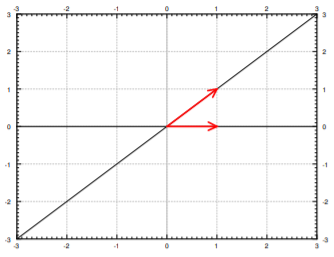
Ahora supongamos que\(x\) y\(y\) están en la línea determinada por un vector propio\( \vec{v} \) para un valor propio\( \lambda \). Es decir,\( \begin{bmatrix} x \\ y \end{bmatrix} = a \vec{v} \) para algunos escalares\(a\). Entonces
\[ \begin{bmatrix} x\\y \end{bmatrix}' = P \begin{bmatrix} x\\y \end{bmatrix} = P(a \vec{v}) = a(P \vec{v}) = a \lambda \vec{v} \nonumber \]
La derivada es un múltiplo de\( \vec{v} \) y por lo tanto puntos a lo largo de la línea determinada por\( \vec{v} \). As\( \lambda > 0 \), la derivada apunta en la dirección de\( vec{v} \) cuando\(\alpha \) es positivo y en sentido contrario cuando\( \alpha\) es negativo. Dibujemos las líneas determinadas por los vectores propios, y dibujemos flechas en las líneas para indicar las direcciones. Ver Figura\(\PageIndex{2}\).
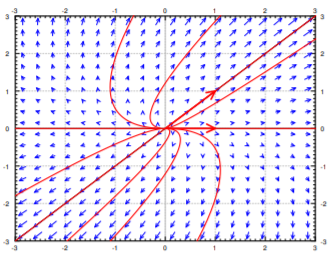
Llenamos el resto de las flechas para el campo vectorial y también dibujamos algunas soluciones. Ver Figura\(\PageIndex{3}\). Observe que la imagen parece una fuente con flechas que salen del origen. De ahí que llamemos a este tipo de imagen una fuente o a veces un nodo inestable.
2
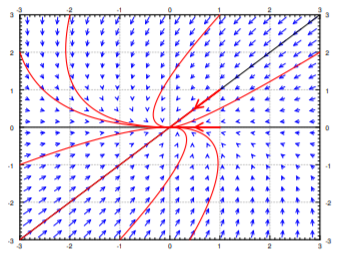
Supongamos que ambos valores propios fueron negativos. Por ejemplo, tomemos la negación de la matriz en el caso 1,\( \begin{bmatrix} -1 & -1\\ 0 & -2 \end{bmatrix} \). Los valores propios son -1 y -2 y los vectores propios correspondientes son los mismos,\( \begin{bmatrix} 1\\0 \end{bmatrix} \) y\(\begin{bmatrix}1\\1\end{bmatrix}\). El cálculo y la imagen son casi los mismos. La única diferencia es que los valores propios son negativos y por lo tanto todas las flechas se invierten. Obtenemos la imagen en Figura\(\PageIndex{4}\). Llamamos a este tipo de imagen un sumidero o a veces un nodo estable.
3
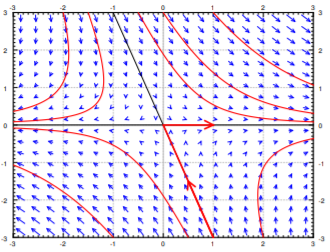
Supongamos que un valor propio es positivo y otro negativo. Por ejemplo la matriz\(\left[\begin{array}{cc}{1}&{1}\\{0}&{-2}\end{array}\right]\). Los valores propios son\(1\) y\(−2\) y los vectores propios correspondientes son\(\left[\begin{array}{c}{1}\\{0}\end{array}\right]\) y\(\left[\begin{array}{c}{1}\\{-3}\end{array}\right]\).
Invertimos las flechas en una línea (correspondiente al valor propio negativo) y obtenemos la imagen en la Figura\(\PageIndex{5}\). Llamamos a esta imagen un punto de silla de montar.
Para los siguientes tres casos asumiremos que los valores propios son complejos. En este caso los vectores propios también son complejos y no podemos simplemente trazarlos en el plano.
4
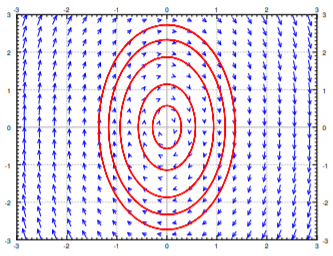
Supongamos que los valores propios son puramente imaginarios. Es decir, supongamos que los valores propios son\(\pm ib\). Por ejemplo, vamos\( P = \begin{bmatrix} 0&1\\-4&0\end{bmatrix} \). Los valores propios resultan ser\(\pm 2i \) y los vectores propios son\( \begin{bmatrix} 1 \\ 2i \end{bmatrix} \) y\(\begin{bmatrix} 1 \\ -2i \end{bmatrix} \). Considere el valor propio\(2i\) y su propio vector\( \begin{bmatrix} 1\\ 2i \end{bmatrix}\). Las partes reales e imaginarias de\(\vec{v} e^{i 2t} \) son
\[ Re \begin{bmatrix} 1\\2i \end{bmatrix} e^{i2t} = \begin{bmatrix} cos(2t)\\-2sin(2t) \end{bmatrix},\quad Im \begin{bmatrix} 1\\2i \end{bmatrix} e^{i2t} = \begin{bmatrix} sin(2t) \\2cos(2t) \end{bmatrix} \nonumber \]
Podemos tomar cualquier combinación lineal de ellos para obtener otras soluciones, cuál tomamos depende de las condiciones iniciales. Ahora tenga en cuenta que la parte real es una ecuación paramétrica para una elipse. Lo mismo con la parte imaginaria y de hecho cualquier combinación lineal de las dos. Esto es lo que sucede en general cuando los valores propios son puramente imaginarios. Entonces, cuando los valores propios son puramente imaginarios, obtenemos elipses para las soluciones. Este tipo de imagen a veces se llama centro. Ver Figura\(\PageIndex{6}\).
5
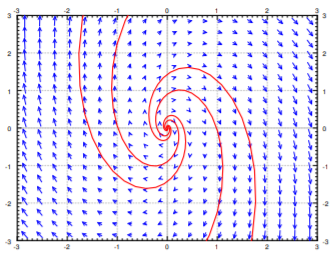
Ahora supongamos que los valores propios complejos tienen una parte real positiva. Es decir, supongamos que los valores propios son\(a \pm ib \) para algunos\(a > 0 \). Por ejemplo, vamos\(P = \begin{bmatrix} 1&1 \\ -4&1 \end{bmatrix} \). Los valores propios resultan ser\( 1 \pm 2i \) y los vectores propios son\( \begin{bmatrix}1\\2i \end{bmatrix} \) y\( \begin{bmatrix} 1 \\ -2i \end{bmatrix}\). Tomamos\(1\pm 2i \) y su propio vector\( \begin{bmatrix} 1 \\ 2i \end{bmatrix} \) y encontramos lo real e imaginario de\(\vec{v}e^{(1+2i)t}\) son
\[ Re \begin{bmatrix} 1\\2i \end{bmatrix} e^{(1+2i)t} =e^t \begin{bmatrix} cos(2t)\\-2sin(2t) \end{bmatrix} \quad Im \begin{bmatrix} 1\\2i \end{bmatrix} e^{(1+2i)t} =e^t \begin{bmatrix} sin(2t) \\2cos(2t) \end{bmatrix} \nonumber \]
Tenga\(e^t\) en cuenta el frente de las soluciones. Esto significa que las soluciones crecen en magnitud mientras giran alrededor del origen. De ahí que obtengamos una fuente espiral. Ver Figura\(\PageIndex{7}\).
6
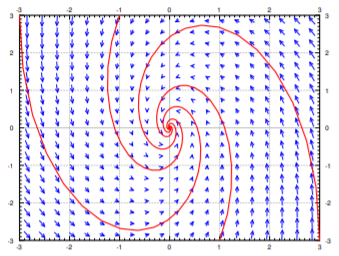
Finalmente supongamos que los valores propios complejos tienen una parte real negativa. Es decir, supongamos que los valores propios son\(-a \pm ib \) para algunos\( a > 0 \). Por ejemplo, vamos\( P = \begin{bmatrix} -1& -1 \\ 4 & -1\end{bmatrix} \). Los valores propios resultan ser\(-1 \pm 2i \) y los vectores propios son\(\begin{bmatrix} 1\\ -2i \end{bmatrix} \) y\(\begin{bmatrix} 1\\ 2i \end{bmatrix}\). Tomamos\( -1-2i \) y su propio vector\(\begin{bmatrix} 1\\ 2i \end{bmatrix}\) y encontramos lo real e imaginario de\(\vec{v} e^{(-1-2i)t} \) son
\[Re \begin{bmatrix} 1\\2i \end{bmatrix} e^{(-1-2i)t} =e^{-t} \begin{bmatrix} cos(2t)\\ 2sin(2t) \end{bmatrix} \quad Im \begin{bmatrix} 1\\2i \end{bmatrix} e^{(-1-2i)t} =e^{-t} \begin{bmatrix} -sin(2t) \\2cos(2t) \end{bmatrix} \nonumber \]
Tenga\(e^{-t}\) en cuenta el frente de las soluciones. Esto significa que las soluciones se contraen en magnitud mientras giran alrededor del origen. De ahí que obtengamos un fregadero en espiral. Ver Figura\(\PageIndex{8}\).
Resumimos el comportamiento de los sistemas bidimensionales homogéneos lineales dados por una matriz no singular en la Tabla\(\PageIndex{1}\). Los sistemas donde uno de los valores propios es cero (la matriz es singular) surgen en la práctica de vez en cuando, ver Ejemplo 3.1.2, y las imágenes son algo diferentes (más simples en cierto modo). Ver los ejercicios.
| Valores propios | Comportamiento |
|---|---|
| reales y ambos positivos | fuente/nodo inestable |
| real y ambos negativos | sumidero/nodo estable |
| signos reales y opuestos | sillín |
| puramente imaginario | punto central/elipses |
| complejo con parte real positiva | fuente espiral |
| complejo con parte real negativa | fregadero espiral |


